Students can Download Maths Chapter 11 Congruency of Triangles Ex 11.5 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 11 Congruency of Triangles Ex 11.5
Question 1.
In ∆ ABC, AC = AB and the altitude AD bisects BC prove that ∆ ADC = ∆ ADB.
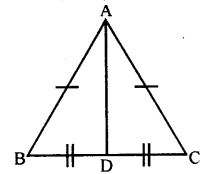
Answer:
In ∆ ABD and ∆ ACD
AB = AC [data]
BD = DC [data]
AD = AD [Common side]
∴ ∆ ABD = ∆ ACD [SSS postulate].
Question 2.
In a square PQRS, diagonals bisect each other at O. Prove that: ∆ POQ = ∆ QOR = ∆ ROS = ∆ SOP
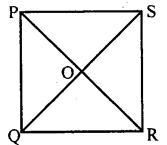
Answer:
∆ POQ and ∆ QOR
PQ = QR [Sides of a square]
PO = OR [data]
OQ = OQ [Common side]
∴ ∆ POQ = ∆ QOR [SSS postulate] …i In AQOR and AROS QR = RS [Sides of a square]
QO = OS [data]
OR = OR [Common side]
∴ ∆ QOR = ∆ ROS [SSS postulate] …ii
In ∆ROS and ∆SOP
SR = SP [Sides of a square]
RO = OP [data]
OS = OS [Common side]
∴ ∆ ROS ≅ ∆SOP [SSSpostulate]…iii
From (i), (ii) and (iii)
∆POQ ≅ ∆QOR ≅ ∆ROS ≅ ∆SOP
Question 3.
In figure two sides AB, BC, and the median AD of ∆ABC are respectively equal to two sides PQ, QR, and median PS of ∆PQR. Prove that
(1) AADB ≅ APSQ
(2) AADC ≅ APSR
Does if follow that triangles ABC and PQR are congruent.
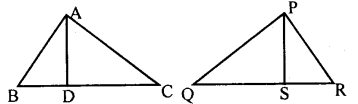
Ans
1. IN ∆ ADB and ∆ PSQ
AB = PQ [data]
BD = QS [BC = QR, D and S are the mid points]
AD = PS [data]
∆ ABD ≅ ∆PQR [SSS postulate]
∠APB = ∠ PSQ [Corresponding sides]
2. ∆ ADC and ∆ PSR
AB = PQ [data]
DC = SR
[BC = QR, D and S are the mid points]
∠ADC =∠PSR
∴[∠ADC = 180 – ∠APB
∠PSR = 180 -∠PSQ
∠ADB =∠PSQ]
∆ ABC ≅ ∆ PSR [SAS postulate]
Yes from the results of (i) and( ii)
∆ ABC = ∆ PQR
Question 4.
In ∆ PQR, PQ = QR, L, M, and N are the midpoint of the sides of PQ, QR, and RP respectively prove that LN = MN
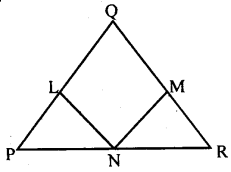
Answer:
PQ = QR [data]
∠P = ∠R [Theorem l]
In ∆ PLN and RMN
PL = RM
[PQ = QR and L and M are the midpoints]
∠P = ∠R
PN = NR [N is the mid point of PR]
∴ ∆ PLN ≅ ∆RMN [SAS postulate]
∴ LN = MN [Corresponding sides]