Students can Download Maths Chapter 14 Introduction of Graphs Ex 14.2 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 14 Introduction of Graphs Ex 14.2
Question 1.
Draw the graphs of the following straight lines.
(i) y = 3 – x
(ii) y = x – 3
(iii) y = 3x – 2
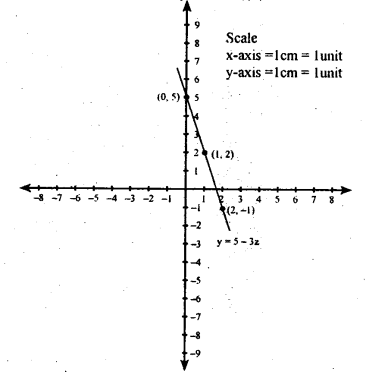
(iv) y = 5 – 3x
(v) 4y = – x + 3
(vi) 3y = 4x + 1
(vii) x = 4
(vii) 3y = 1
Answer:
(i) y = 3 – x
| x | 0 | 1 | 2 |
| y | 3 | 2 | 1 |
When x = 0, y = 3 – 0 = (3)
When x = 1, y = 3 – 1 = (2)
Whenx = 2, y = 3 – 2 = (1)
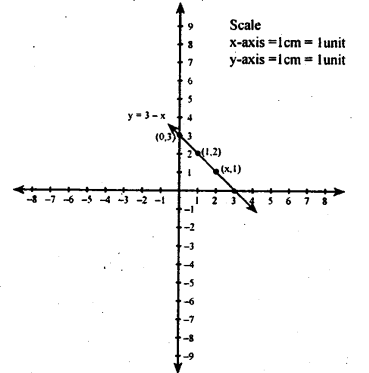
(ii) y = x – 3
| X | 0 | 1 | 2 |
| y | -3 | -2 | -1 |
When x = 0, y = 0 – 3 = (- 3)
When x = 1, y = 1 – 3 = (- 2)
Whenx = 2, y = 2 – 3 = (- 1)
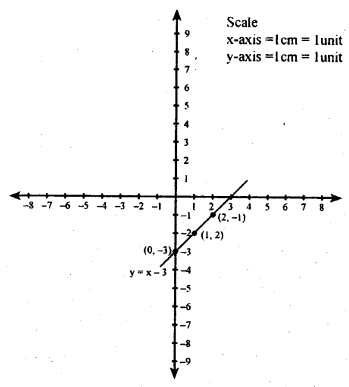
(iii) y = 3x – 2
| X | 0 | 1 | 2 |
| y | -2 | 1 | 4 |
When x = 0, y = 3(0) – 2 = (- 2)
When x = 1, y = 3(1) – 2 = (1)
Whenx = 2, y =3(2) – 2 = (4)
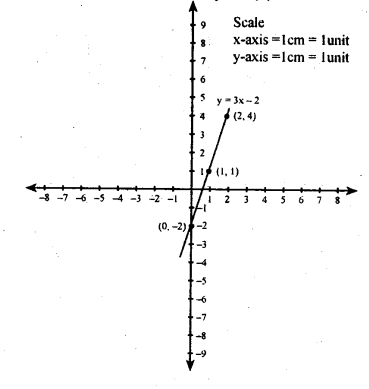
(iv) y = 5 – 3x
| X | 0 | 1 | 2 |
| y | 5 | 2 | -1 |
When x = 0, y = 5 – 3(0) = 5
When x = 1, y = 5 – 3(1) = 2
Whenx = 2, y = 5 – 3(2) = 5 – 6 = -1
(v) 4y = – x + 3

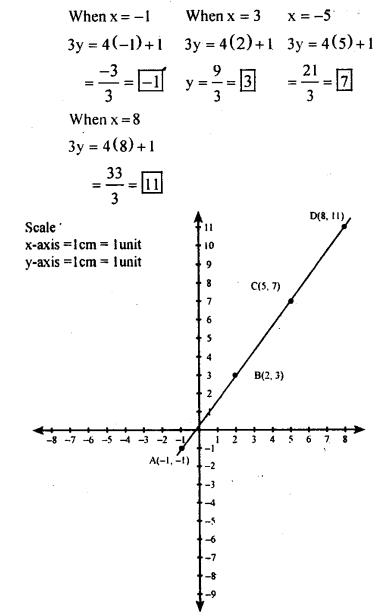
(vi) 3y = 4x + 1
| X | -1 | 2 | 5 | 8 |
| y | -1 | 3 | 7 | 11 |
| (x,y) | (-1,0 | (2,3) | (5,7) | (7,11) |
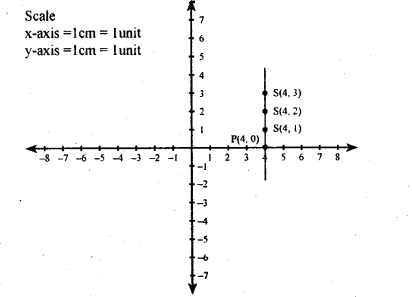
(vii) x = 4
| X | 4 | 4 | 4 | 4 |
| y | 0 | 1 | 2 | 3 |
| (x,y) | (4,0) | (4,0 | (4,2) | (4,3) |
(vii) 3y = 1
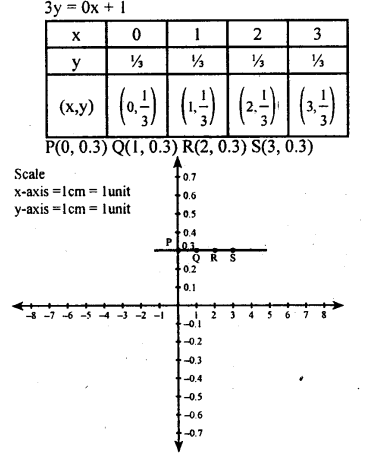
Question 2.
Draw the graph of \(\frac{y}{x}=\frac{y+1}{x+2}\)
Answer:
When x = 1
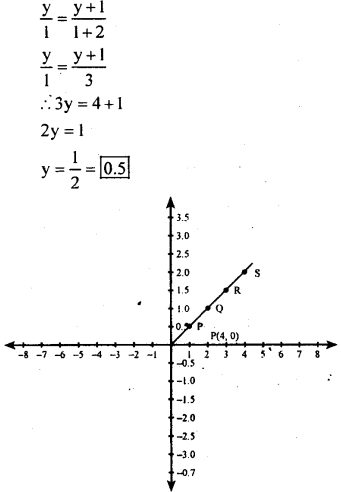
Question 3.
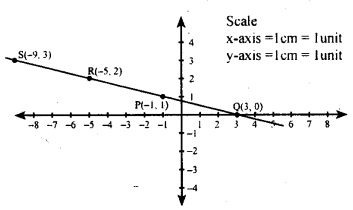
Determine the equation of the line in each of the following graphs
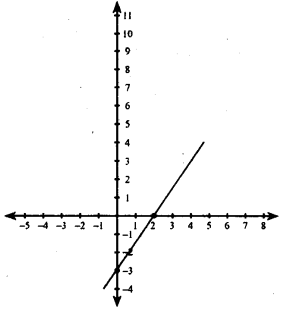
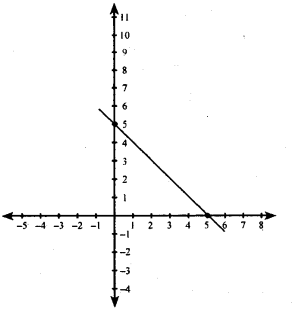
Answer:
(i) Let the equation be y = ax + b
We find that the lines passes through (2,0)
i. e., when x = 2, y = 0
∴ y = ax+b
0 = ax + b
0 = a(2) + b
0 = 2a + b
∴ b = – 2a
The line passes through (4,3) also
i. e., when x=4 , y = 3
∴ y = ax + b
3 = a(4) + b
3 = 4a + b
3 = 4a + (-2a)
3 = 4a = 2a
a = \(\frac { 3 }{ 2 }\) b = – 2a = \(-2 \cdot \frac{3}{2}\) = -3
y = ax + b y
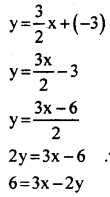
The equation is 3x – 2y = 6
(ii) Let the equation be y = ax + b
we find that the line passes through (5,0) i.e., when x = 5, y = 0
∴ y = ax + b
0 = a(5) + b
0 = 5a + b
b = -5a
The line passes through (0 , 5)also
i.e.,when x = 0, y = 5
y = ax + b
5 = a(0) + b
5 = 0 + b
5 = 0 + (-5a)
5 = -5a
∴ a =
a = -1
b = -5a = -5(-1) = 5 b = 5
b = 5
y=ax + b
y = – 1 x + 5 y = – x + 5 y + x = 5
The equation of the line of is y + x = 6
Question 4.
A boat is moving in a river, downstream, whose stream has speed 8km/ hr. the speed of the motor of the boat is 22km/hr. Draw the graph of the distance covered by the boat versus an hour.
Answer:
Speed of the boat downstream = 22 + 8 = 30 km/hr
y = 30x
| Time | i | 2 | 3 | 4 | 5 |
| Distance | 30 | 60 | 90 | 120 | 150 |
| (1,30) | (2,60) | (3,90) | (4.120) | (5,150) |
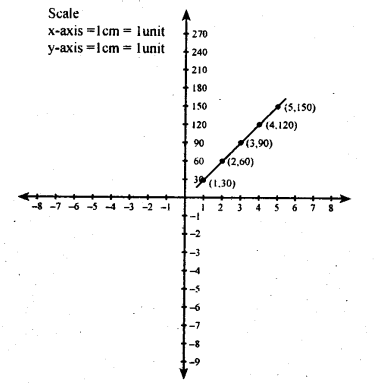
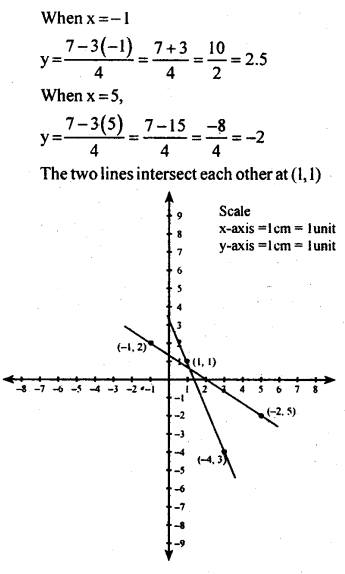
Question 5.
Find the point of intersection of the straight lines 3y + 4x = 7 and 4y + 3x = 7, by drawing their graphs and looking for the point where they meet.
Answer:
3y + 4x = 7
3y = 7 -4x
\(y-\frac{7-4 x}{3}\)
| X | l | 4 |
| y | 1 | -3 |
| (x,y) | (1 × 1) | (4-3) |
When x=1, \(y-\frac{7-4 x}{3}\) = \(\frac{7-4}{3}=\frac{3}{3}=1\)
When x = 4,
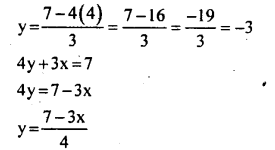
| X | -1 | 5 |
| y | 2.5 | -2 . |
| (x,y) | (-1,2.5) | (5-2) |