Students can Download Maths Chapter 2 Algebraic Expressions Ex 2.4 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 2 Algebraic Expressions Ex 2.4
Question 1.
Find the product:
i. (a + 3) ( a + 5)
ii. (3t + 1) (3t + 4)
iii. (a – 8) (a + 2)
iv. (a – 6) (a – 2)
Answer:
i. (a + 3) (a + 5) This is in the form.
(x + a)(x + b) = x² + (a + b)x + ab
Here x = a, a = 3, b = 5
(a + 3)(a + 5) = a² + (a + 5)a + 3.5
= a² + 8a + 15
(ii) (3t + 1)(3t + 4)This is in the form.
(x + a)(x + b) = x² +(a + b)x + ab
Here x =3t,a = 1, b = 4
(3t – 1)(3t + 4) = (3t)²+(1 + 4)3t + 1.4
= 9t² + 5(3t) + 4 = 9t² + 15t + 4
(iii) (a -8)(a + 2)
This is in the form (x + a)(x + b) = x² + (a + b)x + ab
Here x = a, a = -8, b = 2
(a – 8)(a + 2) = a² + (-8 + 2)a + (-8)(2)
= a² + (-6)a – 16
= a² – 6a – 16
(iv) (a – 6)(a – 2)
This is in the form (x + a)(x + b) = x² +(a + b)x + ab
Herex = a, a = -6,b = -2
(a – 6)(a – 2) = a² + (- 6 – 2) a + (-6)(-2)
=a² + (- 8)a + 12
= a² – 8a + 12
2. Evaluate using suitable identities
Question i.
53 × 55
Answer:
53 × 55 = (50 + 3) (50 + 5)
This is in the form (x + a)(x + b) = x² + (a + b)x + ab
Here x = 50, a = 3, b = 5
(50 + 3)(50 + 5) = 50² + (3 + 5) 50 + 3 × 5
= 2500 + (8)50 +15
= 2500 + 400 + 15
∴ 53 × 55 = 2915
Question ii.
102 × 106
Answer:
102 × 106 = (100 + 2) (100 + 6) This is in the form.
(x + a)(x + b) = x² +(a + b)x + ab
Here x = 100, a = 2, b = 6
(100 + 2)(100 + 6) = 100² +(2 + 6)100 + 2 × 6
= 10000 + (8)100 + 12
= 10000 + 800 + 12
∴102 × 106 = 10812
Question iii.
34 × 36
Answer:
34 × 36 = (30 + 4) (30 + 6) This is in the form.
(x + a)(x + b) = x²+ (a + b)x + ab
Here x =30, a = 4, b = 6
(30 + 4)(30 + 6) = 30² + (4 + 6)30 + 4 × 6
= 900 + 300 + 24
34 × 36 = 1224
Question iv.
103× 96
Answer: 103 × 96 = (100 + 3)(100-4)This is in the form.
(x + a)(x + b) = x² + (a + b)x + ab
Here x = 100,a = 3,b = -4 (100 + 3)(100-4) = 100² + (3 – 4)100 + 3 × -4
= 10000 + (- 1)100 – 12
= 10000 – 100 – 12
103 × 96 = 9888
Question 3.
Find the expression for the product (x+a) (x+b) (x+c) using the identity (x+a)(x+b) = x² + (a + b)x + ab
Answer:
(x + a) (x + b) (x + c)
Consider (x + a)(x + b)
= x² + (a + b)x + ab
= x² + ax + bx + ab (x + a)(x + b)(x + c)
= (x² + ax + bx + ab)(x + c)
= x(x² + ax + bx+ ab) + c
(x² + ax + bx + ab)
= x3 + ax² + bx² + abx + cx² + cax +cbx + abc
= x3 + ax² + bx² + cx² + abx + cax +cbx + abc [by rearranging]
= x3 + x²(a + b + c) + x(ab + ca +bc) + abc
∴ (x + a)(x + b)(x + c)
= x3 +x² (a + b + c) + x(ab + bc + ca) + abc
4. Using the identify (a+b)2 = a² + 2ab+b² simplify the following.
Question i.
(a + 6 )²
Answer:
Using the identity
(a + b)² = a² + 2ab + b²
(a + 6)² = a² +2.a.6 + 6²
= a² +12a + 36
Question ii.
(3x+2y)2
Answer:
Using the identity
(a + b)² = a² +2ab + b²
(3x + 2y)² =(3x)² + 2.3x.2y + (2y)²
= 9x² +12xy + 4y²
Question iii.
(2p + 3q)²
Answer:
Using the identity
(a + b)² =a² + 2ab + b²
(2p + 3q)² =(2p)² +2.2p.3q + (3q)²
= 4p² + 12pq + 9q²
Question iv.
(x² + 5)²
Answer:
Using the identity (a + b)² = a² +2ab + b²
(x² +5)² = (x²)² + 2.x².5 + 52 = x4 + 10x² + 25
5. Evaluate using the identity (a+b)² = a² + 2ab + b²
Question i.
(34)²
Answer:
34² = (30 + 4)²
(a + b)² = a² + 2ab+ b² Here a = 30, b = 4
(30 + 4)² = (30)² + 2 × 30 × 4 + (4)²
= 900 + 240 + 16
(34)² = 1156
Question ii.
(10.2)²
Answer:
(10.2)² = (10 + 0.2)²
(a + b)² = a² + 2ab + b² Here a = 10, b=0.2
[(10 + (0.2))]² = 10² +2.(10).(0.2) + (0.2)² ]
= 100 + 4 + 0.04
(10.2)² = 104.04
Question iii.
53²
Answer:
53² = (50 + 3)²
(a + b)² =a² +2ab + b²
Here a = 50, b = 3 (50 + 3)² =50² + 2 × 50 × 3 + (3)²
= 2500 + 300 + 9
53² = 2809
Question iv.
(41 )²
Answer:
41² = (40 + 1)²
(a + b)² = a² + 2ab + b²
Here a = 40,b = 1
(40 + 1)² = 40² + 2 × 40 × 1 + (1)²
= 1600 + 80 + 1
41² = 1681
6. Use the identify (a -b)² = a² – 2ab + b² to compute.
Question i.
(x – 6)²
Answer:
(a – b)² = a² – 2ab + b²
Herea = x, b=6
(x – 6)² = x² – (2)(x)(6) + 6²
= x² – 12x+ 36
Question ii.
(3x – 5y)²
Answer:
(a – b)² = a² – 2ab + b² Here a = 3x, b = 5y
(3x – 5y)² = (3x)² -(2)(3x)(5y) + (5y)² = 9x² – 30xy + 25y²
Question iii.
(5a – 4b)²
Answer:
(a – b)² = a² – 2ab + b²
Here a = 5a, b = 4b
(5a – 4b)² = (5a)² – (2)(5a)(4b) + (4b)²
= 25a² – 40ab + 16b²
Question iv.
(p² – q²)²
Answer:
(a – b)² = a² – 2ab + b² Here a = p² , b = q2
(p² – q²)² = (p²)² – (2)(p²)(q²) + (q²)²
= p4 – 2p²q² + q4
7. Evaluate using the identify (a – b)² = a² – 2ab + b².
Question i.
(49)²
Answer:
49² = (50 – 1)²
(a – b)² = a² – 2ab + b² Here a = 50, b = 1
(50 – 1)² = 50² – (2)(50)(1) + 1² = 2500 – 100 + 1
(49)² = 2401
Question ii.
(9.8)²
Answer:
(9.8)² = (10 – 0.2)²
(a – b)² =a² – 2ab + b² Here a = 10, b=0.2
(10 – 0.2)² = 10² – (2)(10)(0.2) + (0.2)²
= 100 – 4 + 0.04
(9.8)² =96.04
Question iii.
59²
Answer:
59² = (60 – 1)²
(a – b)² = a² – 2ab + b² Here a = 60, b = 1
(60 – 1)² = 60² – (2)(60)(1) +12 = 3600 – 120 + 1
59² =3481
Question iv.
(198)²
Answer:
(198)² = (200 – 2)²
(a – b)² = a² – 2ab + b² Here a = 200, b = 2
(200 – 2)² = 200² – (2)(200)(2) + 2²
= 40000 – 800 + 4
(198)² = 39204
8. Use the identify (a + b) (a – b) = a² – b² to find the product.
Question i.
(x + 6) (x – 6)
Answer:
(a + b) (a – b) = a2 – b2
Here a = x,b = 6
(x + 6)(x – 6) = x² – 6² = x² – 36
Question ii.
(3x + 5) (3x – 5)
Answer:
(a + b) (a – b) = a² – b²
Here a = 3x, b = 5
(3x + 5)(3x – 5) = (3x)² – (5)²
= 9x² -25
Question iii.
(2a + 4b) (2a – 4b)
Answer:
(a + b) (a – b) = a² – b²
Here a = 2a,b = 4b
(2a + 4b)(2a-4b) = (2a)² – (4b)²
= 4a² – 16b²
Question iv.
\(\left(\frac{2 x}{3}+1\right)\left(\frac{2 x}{3}-1\right)\)
Answer:
(a + b) (a – b) = a² – b²
Here a = \(\frac{2 x}{3}\) ,b = 1
\(\left(\frac{2 x}{3}+1\right)\left(\frac{2 x}{3}-1\right)\) = \(\left(\frac{2 x}{3}\right)^{2}-1^{2}\)
= \(\frac{4 x^{2}}{9}-1\)
9. Evaluate these using identity :
Question i.
55 × 45
Answer:
55 × 45 = (50 + 5) (50 – 5)
Identity (a + b)(a – b) = a² – b²
Here a = 50,b=5
(50 + 5)(50 – 5) = (50)² – 5²
= 2500 – 25
55 × 45 = 2475
Question ii.
33 × 27
Answer:
33 × 27 = (30 + 3) (30 – 3)
identity (a + b)(a – b) = a² – b²
Here a = 30,b = 3
(30 + 3)(30 – 3) = 30² – 3² = 900 – 9
33 × 27 = 891
Question iii.
8.5 × 9.5
Answer:
8.5 × 9.5 = (9 – 0.5) (9 + 0.5)
Here a = 9, b = 0.5
(9 – 0.5)(9 + 0.5) = (9²) – (0.5)² = 81 – 0.25
= 80.75
Question iv.
102 × 98
Answer:
102 × 98 = (100+ 2) (100 – 2)
Identity (a + b)(a – b) = a2 – b2
Here a = 100, b= 2
(100 + 2)(100 – 2) = 100² – 2² =10000 – 4
102 × 98 = 9996
10. Find the product.
Question i.
(x – 3)(x + 3) (x2 + 9)
Answer:
(x – 3)(x + 3) (x2 + 9)
Identity(a + b)(a-b) = a² – b²
= (x² – 3²)(x² + 9)
= (x² – 9)(x² + 9)
= (x²)² – 9²
= x4 – 81
Question ii.
(2a + 3)(2a – 3) (4a² + 9)
Answer:
(2a + 3)(2a – 3) (4a² + 9)
Identity (a + b)(a-b) = a² – b²
= [((2a)² – 3²)(4a²+9)²
= (4a² – 9)(4a² + 9)
= (4a²)² – 9² = 16a4 – 81
Question iii.
(P + 2) (P – 2) (P² + 4)
Answer:
(P + 2) (P – 2) (P² + 4)
Identity (a + b)(a – b) = a² – b²
= (P² – 2²)(P²+ 4)
= (P² – 4)(P² + 4)
= (P²)² – 4² = P4 – 16
Question iv.
\(\left(\frac{1}{2} m-\frac{1}{3}\right)\left(\frac{1}{2} m+\frac{1}{3}\right)\left(\frac{1}{4} m^{2}+\frac{1}{9}\right)\)
Answer:
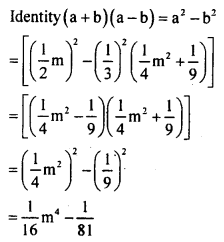
Question v.
(2x – y)(2x + y) (4x² + y²)
Answer:
(2x – y)(2x + y) (4x² + y²)
Identity (a + b)(a – b) = a² – b²
[(2x)² – y²](4x² + y²)
= (4x² – y²)(4x² + y²)
= I6x4 – y4
Question vi.
(2x – 3y)(2x + 3y) (4x² + 9y²)
Answer:
(2x – 3y)(2x + 3y) (4x² + 9y²)
Identity (a + b)(a-b) = a² -b²
= [(2x)² – (3y)²](4x²+ 9y²)
= (4x² – 9y²)(4x² + 9y²)
= (4x²)² – (9y²)²
= 16x4 – 81y4