Students can Download Maths Chapter 3 Axioms, Postulates and Theorems Ex 3.3 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 3 Axioms, Postulates and Theorems Ex 3.3
Question 1.
Find all the angles in the following
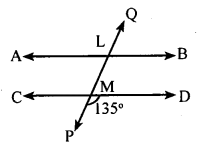
Answer:
∠CMP + ∠PMD = 180° [Linear pair]
∠CMP+ 135° = 180°
∠CMP = 180° – 135
∠CMP = 45°
∠LMD = ∠CMP = 45° [Vertical opposite angles]
∠LMC =∠PMD = 135° [Vertical opposite angles]
∠ALM = ∠ LMC = 135° [Alternate angles]
∠BLM = ∠ LMC = 135° [Alternate angle]
∠QLB = ∠LMD = 45° [Corresponding angles]
∠QLA = ∠ LMC = 135° [Corresponding angles
Question 2.
Find the value of x in the diagram below.
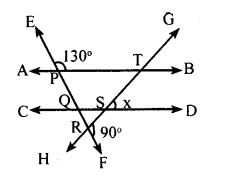
Answer:
∠PQS = ∠EPT = 130° [Corresponding angle]
∠PQS + ∠SQR = 180° [Linear pair]
SQR = 180 – 130
∠SQR = 50°
∠QRS + ∠FRS = 180° [Linear pair]
∠QRS + 90° =180°
∠QRS = 180 – 90
∠QRS = 90°
∠SQR+ ∠QRS +∠QSR = 180°
[Sum of the angles of triangle is 180° ]
50 + 90 + ∠QSR = 180°
140 + ∠QSR = 180°
∠QSR = 180 – 140
∠QSR =40°
∠TSD = ∠QSR [Vertically opposite angles]
x = 40°.
Question 3.
Show that if a straight line is perpendicular to one of the two or more parallel lines, then it is also perpendicular to the remaining lines.
Answer:
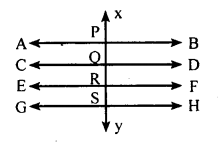
\(\overrightarrow{\mathrm{AB}}\|\overrightarrow{\mathrm{CD}}\| \overrightarrow{\mathrm{EF}} \| \overrightarrow{\mathrm{GH}} \cdot \overline{\mathrm{XY}}\) interrectsthese lines at P, Q, R and S and \(\overrightarrow{\mathrm{XY}} \perp \overline{\mathrm{AB}}\)
Toprove: \(\overline{\mathrm{XY}} \perp \overrightarrow{\mathrm{CD}}, \overline{\mathrm{XY}} \perp \overrightarrow{\mathrm{GH}}\)
Proof :∠XPB = 90° (data)
∠XPB = ∠ PQD = ∠QRF = ∠RSH = 90°
Question 4.
Let \(\overrightarrow{\mathrm{A}} \mathrm{B} \text { and } \overrightarrow{\mathrm{Cb}}\) be two parallel lines and \(\overrightarrow{\mathrm{PQ}}\) be a transversal. Show that the angle bisectors of a pair of two internal angles on the same side of the transversal are perpendicular to each other.
Answer:
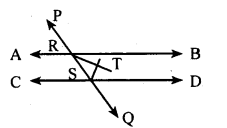
Let the bisectors of ∠BRS and∠RSD intersect at T
To prove: RT⊥ST i.e., ∠RTS = 90°
Proof: ∠BRS +∠RSD = 180°
\(\frac { 1 }{ 2 }\) ∠BRS + \(\frac { 1 }{ 2 }\) ∠RSD = \(\frac { 1 }{ 2 }\) × 180°
\(\frac { 1 }{ 2 }\) ∠BRS = ∠TRS =∠TRB
\(\frac { 1 }{ 2 }\) ∠RSQ = ∠TSR =∠TSD
In triangle TRS,
∠TRS +∠TSR + ∠RTS = 180°
90 + ∠RTS = 180°
∠RTS = 90°
∴ RT ⊥ ST