Students can Download Maths Chapter 6 Theorems on Triangles Ex 6.3 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 6 Theorems on Triangles Ex 6.3
Question 1.
The exterior angles obtained on producing the base of a triangle both ways are 104° and 136°. Find the angles of the triangle.
Answer:
In triangle ABC, BC is produced on either sides.
Let ∠ABC = 140° and ∠ACE = 136°
∠ABD +∠ABC = 180° [ Linear pair]
104 + ∠ABC = 180°
∠ABC = 180 – 104
∠ ABC = 76°
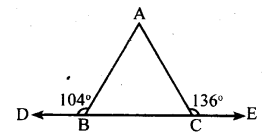
∠ACB + ∠ACE = 180° [Linearpair]
∠ACB + 136° = 180°
∠ACB = 180 – 136 ∠ACB = 44°
∠ABD + ∠ACB + ∠BAC = 180°
[Sum of the angles of a triangle 180° ]
76 + 44 + ∠BAC = 180°
120 + ∠BAC = 180°
∠BAC = 180 – 120 ∠BAC = 60°
Three angles are 76°, 44° & 60°
Question 2.
Sides BC, CA and AB of a triangle ABC are produced in order, forming exterior angles ∠ACD, ∠BAE, and∠CBF.
Show that ∠ACD + ∠BAE + ∠CBF = 360°.
Answer:
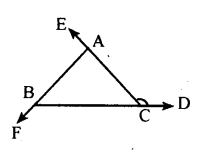
ABC + ∠CBF = 180° [Linear pair]………..(i)
∠ACB + ∠ACD = 180° [Linear pair]……(ii)
∠BAC + ∠BAE = 180° [Linear pair]…….(iii)
Byadding(i), (ii) and (iii)
∠ABC + ∠CBF + ∠ACB + ∠ACD+
∠BAC + ∠BAE = 180 + 180 + 180
∠ABC + ∠ACB + ∠BAC +
∠CBF + ∠ACD + ∠BAE = 540°
180 + ∠CBF + ∠ACD + ∠BAE = 540°
[Sum of the angles of a triangle 180°]
∠CBF + ∠ACD + ∠BAE = 360°
Question 3
Compute the value of x in each of the following figures
Answer:
i.
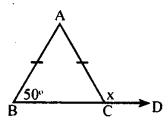
AB = AC
∴ ∠ABC = ∠ACB = 50°
∠ACB + ∠ACD = 180° [Linear pair]
50 + x = 180°
x = 180 – 50 = 130°
ii.
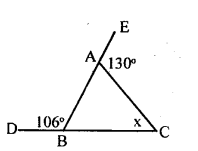
∠ABC + ∠CBF = 180° [Linear pair].
106°+∠ABC = 180°
∠ABC = 180 – 106 = 74°
∠EAC = ∠ABC + ∠ACB
130° =74 +x
130 – 74 = x
∴x = 56°
iii.
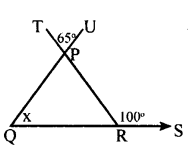
∠QPR = ∠TPU = 65°
[Vertically opposite angles]
∠PRS = ∠PQR + ∠QPR [Exterior angle=Sum of interior opposire angle]
100 = 65 + x
100 – 65 = x
35 = x
∴ x = 35°.
iv.
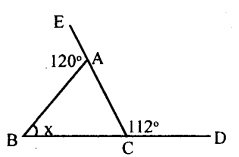
∠BAE + ∠BAC = 180° [Linear pair]
120° + ∠BAC = 180°
∠BAC = 180 – 120
∠BAC = 60°
∠ACD = ∠BAC + ∠ABC
[Exterior angle = Sum of interior opposuite angle]
112° = 60+x
112 – 60 = x
52 = x
x = 52°
v.
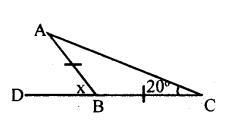
In Δ ABC, BA = BC (data)
∴ ∠BAC = ∠BCA = 20°
[Base angles of an isosceles traingle]
∠ABD = ∠BAC + ∠BCA
[Exterior angle=Sum of interior opposite angle]
x = 20 + 20
x=40°
Question 4.
In figure QT ⊥ PR, ∠TOR = 40° and ∠SPR = 30° find ∠TRS and ∠PSQ.
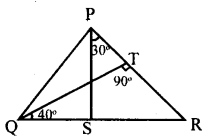
Answer:
In ΔTQR,
∠TQR + ∠QTR + ∠TRQ = 180°
40 + 90 + ∠TRQ = 180°
130 + ∠TRQ = 180
∠ TRQ = 180 – 130
∠ TRQ = 50°
∠ TRS = 50° [∠PRS is same as ∠TRS ]
In Δ PRS, RS is produced to Q
∴Exterior∠PSQ = ∠SPR + ∠PRS = 30 + 50
∠PSQ = 80°
Question 5.
An exterior angle of a triangle is 120° and one of the interior opposite angle is 30 °. Find the other angles of the triangle.
Answer:
In Δ ABC, BC is produced to D. Let
∠ACD = 120° and ∠ABC = 30°
Exterior ∠ACD = ∠BAC + ∠ABC
120 = ∠BAC + 30
120 – 30 = ∠BAC
90° = ∠BAC
∴∠BAC = 90
∠ACB +∠ACD = 180° [Linear pair]
∠ACB + 120 = 180°
∠ACB = 180 – 120
∠ACB = 60°
Other two angles are 90° & 60°