KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2 are part of KSEEB Solutions for Class 9 Maths. Here we have given Karnataka Board Class 9 Maths Chapter 1 Number Systems Exercise 1.2.
Karnataka Board Class 9 Maths Chapter 1 Number Systems Ex 1.2
Question 1.
State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
Answer:
True. Because set of real numbers contain both rational and irrational number.
(ii) Every point on the number line is of the form \(\sqrt{\mathrm{m}}\). where’m’ is a natural number.
Answer:
False. Value of \(\sqrt{\mathrm{m}}\) is not netagive number.
(iii) Every real number is an irrational number.
Answer:
False. Because set of real numbers contain both rational and irrational numbers. But 2 is a rational number but not irrational number.
Question 2.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rationed number.
Answer:
Square root of all positive integers is not an irrational number.
E.g. \(\sqrt{\mathrm{4}}\) = 2 Rational number.
\(\sqrt{\mathrm{9}}\) = 3 Rational number.
Question 3.
Show how \(\sqrt{\mathrm{5}}\) can be represented on the number line.
Answer:
\(\sqrt{\mathrm{5}}\) can be represented on number line:
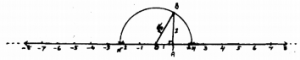
In the Right angled ∆OAB ∠OAB = 90°.
OA = 1 cm, AB = 2 cm., then
As per Pythagoras theorem,
OB2 =OA2 + AB2
= (1)2 + (2)2
= 1 + 4
OB2 = 5
∴ OB = \(\sqrt{\mathrm{5}}\)
If we draw semicircles with radius OB with ‘O’ as centre, value of \(\sqrt{\mathrm{5}}\) on number line
\(\sqrt{\mathrm{5}}\) = OM = +2.3
and \(\sqrt{\mathrm{5}}\) = ON = -2.3 (accurately).
Question 4.
Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion.
Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P22 perpendicular to OP1 of unit length (see fig.). Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn-1Pn by drawing a line segment of unit length perpendicular to OPn-1. In this manner, you will have created the points P2, P3, …………….. pn, …………… and joined them to create a beautiful spiral depicting \(\sqrt{2} \cdot \sqrt{3}, \sqrt{4}, \dots \dots\)
Answer:
Classroom activity :
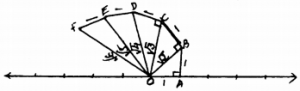
i) OA = 1 Unit, AB = 1 Unit, ∠A = 90°,
∴OB2 = OA2 + AB2
= (1)2 + (1)2
= 1 + 1
OB2 = 2
∴OB = \(\sqrt{2}\)
Similarly, square root spiral can be continued.
We hope the KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2 help you. If you have any query regarding Karnataka Board Class 9 Maths Chapter 1 Number Systems Exercise 1.2, drop a comment below and we will get back to you at the earliest.