KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3 are part of KSEEB Solutions for Class 9 Maths. Here we have given Karnataka Board Class 9 Maths Chapter 1 Number Systems Exercise 1.3.
Karnataka Board Class 9 Maths Chapter 1 Number Systems Ex 1.3
Question 1.
Write the following in decimal form and say what kind of decimal expansion each has :
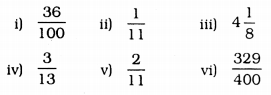
Answer:
(i)

Terminating decimal expansion.
(ii)
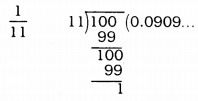
Non-terminating decimal expansion.
\(\begin{aligned} \therefore \quad \frac{1}{11} &=0.090909 \ldots \\ &=0 . \overline{09} \end{aligned}\)
(iii)
∴ Terminating decimal expansion.
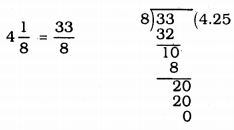
(iv)
\(0 . \overline{23069}\) the bar above the digits indicates the block of digits that repeats.
∴ This is Non-terminating, repeating decimal.
(v)

Here, \(0 . \overline{18}\) is block of digits that repeats.
∴ This is non-terminating, repeating decimal.
(vi)

\(\frac{329}{400}=0.8225\) This is terminating decimal because remainder is zero.
Question 2.
You know that\(\frac{1}{7}=0 . \overline{142857}\). Can you predict what the decimal expansions of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) doing the long division ? If so, how? (Hint: Study the remainders while finding the value of \(\frac{1}{7}\) carefully.).
Answer:
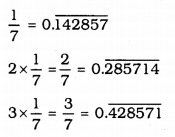
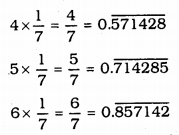
Here the first digit in decimal continued repeated numbers afterward.
Question 3.
Express the following in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0. (p, q ϵ Z, q ≠ 0).
(i) \(0 . \overline{6}\)
(ii) \(0 . \overline{47}\)
(iii) \(0 . \overline{001}\)
Answer:
(i) \(0 . \overline{6}\) = 0.6666……….
Let x = 0.6666………….
∴ x = 0.6666………..
Multiplying both sides by 10,
10x = 6.666…..
10x = 6 + 0.666
10x = 6 + x
10x – x = 6
9x = 6
\(x=\frac{6}{9}=\text { form of } \frac{\mathrm{p}}{\mathrm{q}}\)
∴ \(0 . \overline{6}=\frac{2}{3}\)
(ii) \(0 . \overline{47}\) = 0.4777…..
Let x = \( 0 . \overline{47}\) then x = 0.4777……..
Here digit 4 is not repeating but 7 is repeated.
Let x = 0.4777
Multiplying both sides by 10.
10x = 4.3 + x
10x -x = 4.3
9x = 4.3
Multiplying both sides by 10.
90x = 43
∴ \(0.4 \overline{7}=\frac{43}{90}\)
(iii) \(0 . \overline{001}\) x = 0.001001……….
Multiplying both sides by 1000
1000x = 1.001001
1000x = 1 + x
1000x – x = 1
999x = 1
\(x=\frac{1}{999}\)
∴ \(0 . \overline{001}=\frac{1}{999}\)
Question 4.
Express 0.99999…….. in the form \(\frac{p}{q}\) , Are you surprised by your answer ? With your teacher and classmates discuss why the answer makes sense.
Answer:
Express 0.99999 in the form of \(\frac{p}{q}\),
Let x = 0.99999 …
Multiplying by 10.
10x = 9.9999……
10x = 9 + 0.9999…….
10x = 9 + x
10x – x = 9
9x = 9
\(x=\frac{9}{9}, x=1=\frac{1}{1}\)
∴ (p = 1 & q = 1)
0.99999 …… goes on forever, so there is no gap between 1 and 0.99999 ………… hence they are equal.
Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\) ? Perform the division to check your answer:
Answer:
Expansion of \(\frac{1}{17}\) in decimal:

\(\therefore \quad \frac{1}{17}=0 . \overline{0588235294117647}\)
Here repeated numbers are 16.
Question 6.
Look at several examples of rational numbers in the form \(\frac{p}{q}\) (q≠0), where p
and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Answer:
Rational numbers in the form \(\frac{p}{q}\) (q ≠ 0) where P and q are integers with no common factors other than 2 or 5 or both.
OR
Prime factors of q have powers of 2 and prime factors of q have powers of 5 or both.
Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Answer:
Three numbers whose decimal expansions are non-terminating, non-recurring are
i) 0.123123312333
ii) 0.20200200020000
iii) 0.56566566656666
Question 8.
Find three different irrational numbers between the rational numbers \(\frac{5}{7}\) & \(\frac{9}{11}\) .
Answer:
\(\frac{5}{7}=0 . \overline{714285} \quad \frac{9}{11}=0 . \overline{81}\)
Three irrational numbers between \(0 . \overline{714285}\) and \(0 . \overline{81}\) are :
i) 0.72720720072000………….
ii) 0.7357355735555……………..
iii) 0.760760076000………………
Question 9.
Classify the following numbers as rational or irrational :
(i) \(\sqrt{23}\)
(ii) \(\sqrt{225}\)
(iii) 0.3796
(iv) 7.478478
(v) 1.101001000100001…
Answer:
i) \(\sqrt{23}\) = 4.7958………. This is not terminating or non-recurring decimal.
∴ \(\sqrt{23}\) is an irrational number.
ii) \(\sqrt{23}\) = 15 this is a rational number.
iii) 0.3796 This is rational number, because trminating decimal has expansion.
iv) 0.478478… This is rational number, because decimal expansion is recurring.
v) 0.101001000100001… This is an irrational number because termianting or recruring decimal has no expansion.
We hope the KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3 helps you. If you have any query regarding Karnataka Board Class 9 Maths Chapter 1 Number Systems Exercise 1.3, drop a comment below and we will get back to you at the earliest.