KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 are part of KSEEB Solutions for Class 9 Maths. Here we have given Karnataka Board Class 9 Maths Chapter 1 Number Systems Exercise 1.5.
Karnataka Board Class 9 Maths Chapter 1 Number Systems Ex 1.5
Question 1.
Classify the following numbers as rational or irrational.
Answer:
i) \(2-\sqrt{5}\)
ii) \((3+\sqrt{23})-\sqrt{23}\)
iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
iv) \(\frac{1}{\sqrt{2}}\)
v) 2π
Answer:
i) \(2-\sqrt{5}\) = 2 – 2.2360679……….. = -0.2360679
This is a non-terminating, non-recurring decimal.
∴ This is an irrational number.
ii) \((3+\sqrt{23})-\sqrt{23}\)
= \(3+\sqrt{23}-\sqrt{23}\)
= 3
⇒ \(\frac{3}{1}\). This can be written in the form of \(\frac{p}{q}\).
∴ This is a rationl number.
iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2 \sqrt{7}}{\sqrt{7}}=2 \Rightarrow \frac{2}{1}\)
This can be written in the form of \(\frac{p}{q}\)
∴ This is a rational number.
iv) \(\frac{1}{\sqrt{2}}\)
\(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{1.4142}{2}\)
= 0.707106…………
This is a non-terminating, non-recurring decimal.
∴ This is an irrational number.
v) 2π
= 2 × 3.1415…..
= 6.2830…….
This is a non-terminating, non-recurring decimal.
∴ This is an irrational number.
Question 2.
Simplify each of the following expressions:
i) \((3+\sqrt{3})(2+\sqrt{2})\)
ii) \((3+\sqrt{3})(3-\sqrt{3})\)
iii) \((\sqrt{5}+\sqrt{2})^{2}\)
iv) \((\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})\)
Answer:
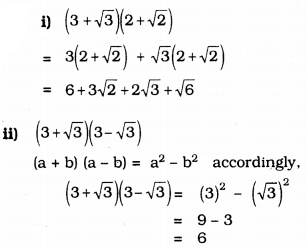
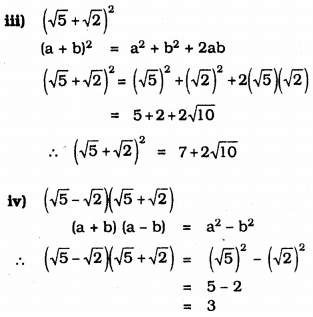
Question 3.
Recall, 2π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, \(\pi=\frac{c}{d}\). This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Answer:
There is no contradiction. When we measure a length with a scale or any other device we get the quotient.
Therefore we cannot judge whether c is a rational number of d is an irrational number.
∴ Value of \(\frac{c}{d}\) is irrational number.
∴ The value of π is also an irrational number.
Question 4.
Represent \(\sqrt{9.3}\) on the number line.
Answer:
Construction: Mark the distance 9.5 units from a fixed point O such that OB = 9.3 units. Mark midpoint D of OC. Draw a semicircle with centre D. Draw a line perpendicular to OC passing through E and intersecting the semicircle at E. Draw an arc BE which intersect at F. Now, BF = \(\sqrt{9.3}\).
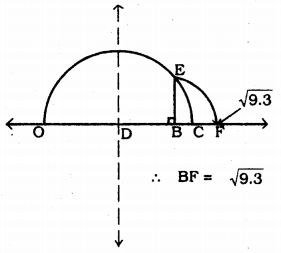
Question 5.
Rationalise the denominators of the following :
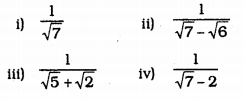
Answer:
i) \(\frac{1}{\sqrt{7}}\)
Denominator’s factor is \(\sqrt{7}\) Mulitplying Numerator and denominator by \(\sqrt{7}\).
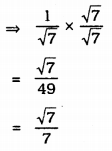
ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
Denominator’s factor is \(\sqrt{7}+\sqrt{6}\)
Multiplying numerator and denominator by \(\sqrt{7}+\sqrt{6}\),
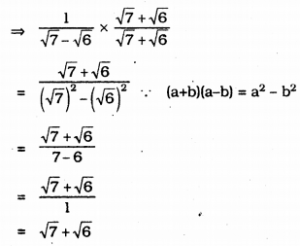
iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
Denominator’s factor is \(\sqrt{5}-\sqrt{2}\)
Multiplying numerator and denominator by \(\sqrt{5}-\sqrt{2}\).
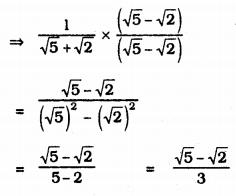
iv) \(\frac{1}{\sqrt{7}-2}\)
Denominator’s factor is \(\sqrt{7}+2\)
Multiplying numerator and denominator by \(\sqrt{7}+2\).
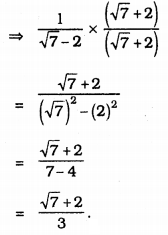
We hope the KSEEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 help you. If you have any query regarding Karnataka Board Class 9 Maths Chapter 1 Number Systems Exercise 1.5, drop a comment below and we will get back to you at the earliest.