Karnataka Board Class 9 Maths Chapter 12 Circles Ex 12.4
Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
R = 5 cm, r = 3 cm. d = 4 cm.
length of the common chord = ?
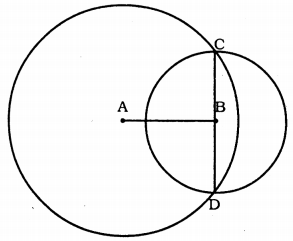
When measured Chord CD = 6 cm.
Circles with centre A and B, intersect at points C and D.
CD is common chord.
Perpendicular bisector of CD is AB.
AC = 5cm. BC = 3cm.
∴ Chord, CD= 2 × OC = 2 × 3
∴ Chord, CD = 6 cm.
Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Data : Circle with centre ‘O’, AB and CD chords are equal and intersect at E.
To Prove: Segment EAD = Segment ACB.
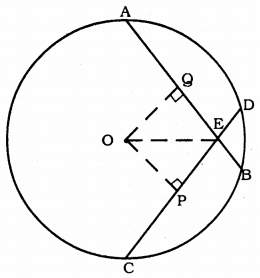
Construction: Draw OP⊥CD and OQ⊥AB.
Join OE.
Proof: AQ = QB (∵ Chord drawn perpendicular CP = PD ,to centre bisects chord.).
In ∆OPE and ∆OQE,
∠OPE = ∠OQE = 90° (Construction)
OP = OQ
OE is common.
∴ ∆OPE ≅ ∆OQE (RHS Theorem)
QE = PE ……….. (i)
But QB = PD
∴ QB – QE = PD – PE
EB = ED ……….. (ii)
From (i) and (ii),
AE = CE.
CBD is minor segment formed by Chord CD.
ADB is minor segment formed by Chord AB.
∴ Minor segment CBD = Minor segment ADB
Major segment CAD = Major segment ACB.
Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords
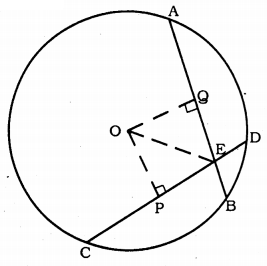
Solution:
Data: O is the centre of Circle. Chord AB = Chord CD. These chords intersects at E. OE is joined.
To Prove: ∠OEP = ∠OEQ Construction:
Draw OP⊥CD and OQ⊥AB.
Proof: In ∆OPE and ∆OQE,
∠OPE = ∠OQE = 90° (construction)
OE is common.
OP = OQ (Equal chords are equidistant)
∴ ∆OPE ≅ ∆OEQ (RHS postulate)
∴ ∠OEP = ∠OEQ.
Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD.
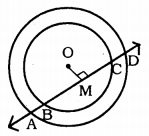
Solution:
Data: A line intersects two concentric circles with centre O at A, B, C, and D.
To Prove: AB = CD.
Construction: Draw OM⊥AD.
Proof: AD is the chord of a bigger circle.
OM⊥AD
∴ AM = MD ………(i) (∵ Perpendicular bisects the chord from centre)
Similarly, BC is the chord of the smaller circle.
OM⊥BC.
∴ BM = MC ………. (ii)
Subtracting (ii) from (i),
AM – BM = MD – MC
∴ AB = CD.
Question 5.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution:
Data: Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 cm drawn in a park. Distance between Reshma and Salma and between Salma and Mandip is 6 cm. each.
To Prove: Distance between Reshma and Mandip = ?, RM = ?
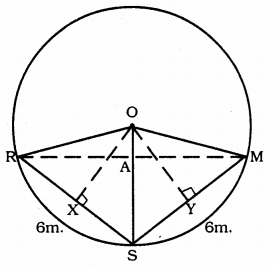
Construction: Draw OX⊥RS and OY⊥SM. OR, OS and OM are joined.
Proof: OR = OS = OM = 5 m.
RX = XS = 3 m.
Now, in ⊥∆ORX,
OR2 = OX2 + RX2
(5)2 = (OX)2 + (3)2
25 = OX2 + 9
25 – 9 = OX2
16 = OX2
OX2 = 16
∴ OX = 4 WI …………… (i)
In quadrilateral ORSM,
OR = OM and SR = SM
∴ ORSM is a kite.
Diagonals of a kite bisect at the right angle.
∠RAS = 90°
∴ RA = AM.

Now, RM = 2RC = 2 × 4.8 = 9.8 m
∴ RM = 9.8 m.
∴ Distance between Reshma and Mandip is 9.8 m.
Question 6.
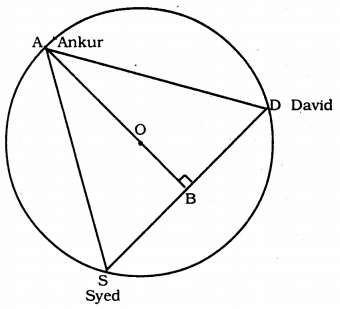
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution:
Data: A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed, and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other.
To Prove: Length of wire of telephone =?
Proof: In this figure, AS = SD = DA
∴ ASD is an equilateral triangle.
∴ OA = 20 m. (∵ radius)
Median passed through centre of circle.
∴ AB is the median.
AD ⊥ SD
Median of an equilateral triangle divides in the ratio 2 : 1 in the centre?
∴ AO : OB = 2 : 1


KSEEB Solutions for Class 9 Maths