KSEEB Solutions for Class 9 Maths Chapter 3 Lines and Angles Ex 3.3 are part of KSEEB Solutions for Class 9 Maths. Here we have given Karnataka Board Class 9 Maths Solutions Chapter 3 Lines and Angles Exercise 3.3.
Karnataka Board Class 9 Maths Chapter 3 Lines and Angles Ex 3.3
Question 1.
In Fig. 3.39, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
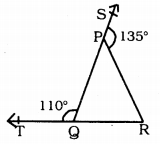
Answer:
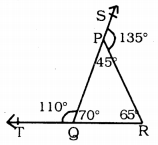
Arms of the ∆PQR QP and RP are produced to S and T and ∠PQT = 110°, ∠SPR = 135°. ∠PRQ =?
Straight-line PR is on straight line SQ.
∠SPR and ∠RPQ are Adjacent angles.
∴ ∠SPR + ∠RPQ = 180°
135 + ∠RPQ = 180°
∴ ∠RPQ =180 – 135
∠RPQ = 45° (i)
Similarly QP straight line is on straight line TR.
∠TQP and ∠PQR are Adjacent angles.
∴ ∠RQP + ∠PQR = 180°
110 + ∠PQR = 180°
∠PQR = 180 – 110
∴ ∠PQR = 70°
Now, in ∆PQR,
∠QPR + ∠PQR + ∠PRQ = 180°
45 + 70 + ∠PRQ = 180°
115 + ∠PRQ = 180°
∠PRQ = 180 – 115
∴ ∠PRQ = 65°.
Question 2.
In Fig. 3.40, ∠X = 62°. ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ
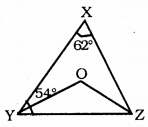
Answer:
In this figure, ∠X = 62°
∠XYZ = 54°
In ∆XYZ, YO and ZO are angular bisectors of ∠XYZ and ∠XZY.
Then, ∠OZY =?
∠OYZ =?
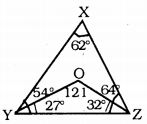
In ∆XYZ
∠X + ∠Y + ∠Z = 180°
62 + 54 + ∠Z= 180
116 + ∠Z= 180
∠Z= 180- 116
∴ ∠Z = 64°
YO is the angular bisector of ∠Y
∴ ∠OYZ = \(\frac{54}{2}\) = 27°
ZO is the angular bisector of ∠Z
∴ ∠OZY = \(\frac{64}{2}\) = 32°
∴ ∠OZY = 32°
Now, in ∆OYZ,
∠OYZ + ∠OZY + ∠YOZ = 180°
27 + 32 + ∠YOZ = 180
59 + ∠YOZ = 180
∠YOZ = 180 – 59
∴∠YOZ = 121°
∴ ∠OZY = 32°
∠YOZ = 121°
Question 3.
In Fig. 3.41, if AB||DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
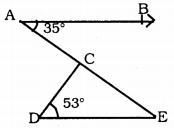
Answer:
If AB || DE, ∠BAC = 35, ∠CDE = 53 then ∠DCE = ?
AB || DE, AE is the bisector.
∴∠BAC = ∠DEC = 35° (∵ Alternate angles)
∴∠DEC= 35°
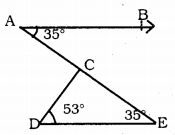
Now in ∆CDE,
∠DCE + ∠CDE + ∠CED = 180°
∠DCE + 53 + 35 = 180
∠DCE + 88 = 180
∠DEC = 180 – 88
∴ ∠DCE = 92°.
Question 4.
In Fig. 3.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
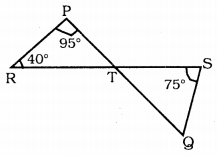
Answer:
PQ and RS straight lines intersect at T.
If ∠PRT = 40°, ∠RPT = 95°, and ∠TSQ = 75°, then ∠SQT =?
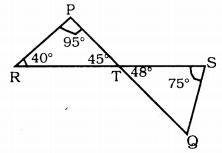
In ∆PRT,
∠RPT + ∠PRT + ∠PTR = 180°
95 + 40 + ∠PTR = 180°
135 + ∠PTR = 180
∠PTR = 180 – 135
∴ ∠PTR = 45°
∠PTR = ∠STQ = 45° (∵ Vertically opposite angles)
In ∆TSQ,
∠STQ + ∠TSQ + ∠SQT =180
45 + 75 + ∠SQT = 180
120 + ∠SQT = 180
∴∠SQT = 180 – 120
∴ ∠SQT = 60°.
Question 5.
In Fig. 3.43, PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°. then find the value of x and y.
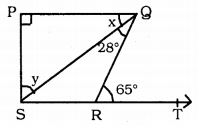
Answer:
PQ ⊥ PS, PQ ⊥ SR, ∠SQR = 28°, ∠QRT = 65°, Then x = ?, y = ?
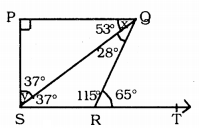
Solution: ∠QRT + ∠QRS = 180° (∵ Linear pairs)
65 + ∠QRS = 180
∠QRS = 180 – 65
∴∠QRS =115°
In ∆SRQ,
∠QRS + ∠SQR + ∠RSQ = 180°
115 + 28 + ∠RSQ = 180
∴∠RSQ =180 – 143
∴∠RSQ = 37
Now, ∠RSQ = ∠PQS
37° = x
∴x = 37
In ∆SPQ,
∠SPQ + ∠PSQ + ∠PQS = 180°
90 + y + 37 = 180
∴y = 180- 127
∴y = 53°.
Question 6.
In Fig. 3.44, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = \(\frac{1}{2}\)∠QPR.
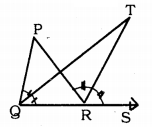
Answer:
Data: Arm QR of ∆PQR is produced upto S. Angular bisectors of ∠PQR and ∠PRS meet at T.
To Prove: ∠QTR = \(\frac{1}{2}\) ∠QPR
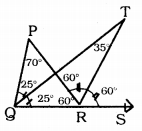
Proof: Let ∠PQR = 50°, and ∠PRS = 120°
∠PQT = ∠TQR = 25°
∠PRT = ∠TRS = 60°
QR arm of ∆ PQR is produced upto S.
∴Exterior angle ∠PRS = ∠PQR + ∠QPR
120 = 50 + ∠QPR
∴ ∠QPR = 120 – 50
∠QPR = 70°
∴ ∠PRQ = 60°
Now, in ∆TRQ,
∠TQR + ∠TRQ + ∠QTR = 180°
25 + 120 + ∠QTR = 180°
145 + ∠QTR = 180°
∠QTR = 180 – 145
∴ ∠QTR = 35°
Now, ∠QTR = 35° ∠QPR = 70°
∠QTR = \(\frac{70}{2}\)
∴ ∠QTR = \(\frac{10}{2}\) x ∠QPR.
We hope the KSEEB Solutions for Class 9 Maths Chapter 3 Lines and Angles Ex 3.3 help you. If you have any query regarding Karnataka Board Class 9 Maths Chapter 3 Lines and Angles Exercise 3.3, drop a comment below and we will get back to you at the earliest.