Students can Download Class 10 Maths Chapter 10 Quadratic Equations Additional Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 10 Maths Chapter 10 Quadratic Equations Additional Questions
I. Multiple Choice Questions:
Question 1.
The degree of a quadratic equations is
a. 1
b. 2
c. 3
d. 4
Answer:
b. 2
![]()
Question 2.
The standard form of quadratic equation is
a. ax2 + bx + c = 0
b. ax + c = 0
c. ax3 + bx2 + c = 0
d. ax4 + bx3 + cx2 + dx + c= 0
Answer:
a. ax2 + bx + c = 0
Question 3.
The standard form of pure quadratic equation is
a. ax2 + bx + c = 0
b. ax2 + c = 0
c. ax3 + bx2 + cx = 0
d. ax4 + bx3 + cx2 + dx + c= 0
Answer:
b. ax2 + c = 0
Question 4.
An quadratic equation has only
a. 1 root
b. 2 roots
c. 3 roots
d. 4 roots
Answer:
b. 2 roots
Question 5.
The roots of the quadratic equation 3x2 – 6x = 0 are
a. (0, 2)
b. (3, 6)
c. (0, – 2)
d. (0, 6)
Answer:
a. (0, 2)
Question 6.
The roots of the quadratic equation (2x + 1)( 3x – 5) = 0 are
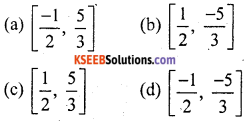
Answer:
a. \(\left[\frac{-1}{2}, \frac{5}{3}\right]\)
Question 7.
The roots of the quadratic equation 3x2 = 36 are
a. ±2\(\sqrt{3}\)
b. ±3\(\sqrt{2}\)
c. ±12
d. ±\(\sqrt{2}\)
Answer:
a. ±2\(\sqrt{3}\)
![]()
Question 8.
The consecutive even integers are
a. (2x) (x + 2)
b. (x) (x + 2)
c. (x) (x + 1)
d. (x) (x – 1)
Answer:
b. (x) (x + 2)
Question 9.
Two consecutive positive integers differ by
a. 2
b. 1
c. 3
d. 4
Answer:
b. 1
Question 10.
The sum of the squares of two consecutive natural numbers is 25 represent this statement in the form of a quadratic equation.
a. x2 + (x + 1)2 = 25
b. x2 – (x – 1)2 = 25
c. (x + 1) – x2 = 25
d. x2 + (x + 1)2 + 25 = 0
Answer:
a. x2 + (x + 1)2 = 25
Question 11.
The discriminant of the quadratic equation ax2 + bx + c = 0 is
a. ∆ = b2 + 4ac
b. ∆ = b2 – 4ac
c. ∆ = 4abc
d. ∆ = b2 × 4ac
Answer:
b. ∆ = b2 – 4ac
Question 12.
The nature of the roots of the quadratic equation 2x2 – 4x + 3 = 0 are
a. real and distinct
b. real and equal
c. no real roots
d. imaginary
Answer:
d. imaginary
![]()
Question 13.
If k = \(\frac{1}{2}\) mv2 then v is equal to

Answer:
a. ±\(\sqrt{\frac{2 \mathrm{k}}{\mathrm{m}}}\)
Question 14.
If ax2 + bx + c = 0 then quadratic formula is
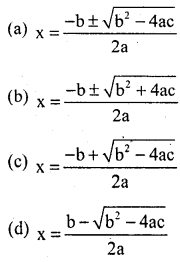
Answer:
a. x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Question 15.
The quadratic equation whose roots are 2 and 3 is
a. x2 + 5x + 6 = 0
b. x2 – 5x + 6 = 0
c. x2 – 5x – 6 = 0
d. x2 + 5x – 6 = 0
Answer:
b. x2 – 5x + 6 = 0
![]()
Question 16.
The sum of the roots of the equation 2x2 – 8 = 0 is
a. 2
b. 4
c. – 4
d. 0
Answer:
d. 0
Question 17.
The product of the equation 3x2 = 9x is
a. 0
b. – 3
c. 2
d. 9
Answer:
a. 0
Question 18.
If l2 = r2 + d2 then the value of d is equal to
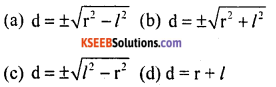
Answer:
c. d = ±\(\sqrt{l^{2}-r^{2}}\)
Question 19.
The name of the graph of y = 2x + 3 is called
a. Parabola
b. Hyper bola
c. Straight line
d. Bar graph
Answer:
c. Straight line
![]()
Question 20.
The name of the graph y = mx + c is called
a. Straight line
b. Parabola
c. Hyper bola
d. Pie chart
Answer:
a. Straight line
II. Short Answer Questions:
Question 1.
Write the standard form of Quadratic equation
Answer:
ax2 + bx + c = 0
Question 2.
If b2 – 4ac < 0, then find the nature of roots of Quadratic equation ax2 + bx + c = 0.
Answer:
Roots are imaginary
Question 3.
Write the standard form of the equation \(\frac{6}{x}+\frac{x}{1}\) = 5
Answer:
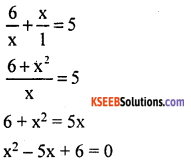
Question 4.
If 7y = \(\frac{35}{y}\) then find the value of y.
Answer:
7y = \(\frac{35}{y}\)
7y2 = 35

Question 5.
Find the discriminant of x2 + 5x + 5 = 0
Answer:
x2 + 5x + 5 = 0
It is in the form of ax2 + bx + c = 0
a = 1, b = 5 and c = 5
∆ = b2 – 4ac
= (5)2 – 4 (1) (5) = 25 – 20
∆ = 5
Discriminant = 5
![]()
Question 6.
Solve 5x2 = 625
Answer:
5x2 = 625
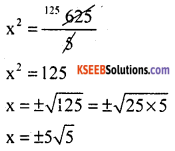
Question 7.
Write the formula to find the roots of Quadratic equation ap2 + bp + c = 0
Answer:
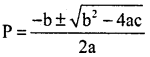
Question 8.
Is x = – 2 is a solution of 3x2 + 13x + 14 = 0
Answer:
LHS 3x2 + 13x + 14
= 3 (- 2)2 + 13 (- 2) + 14
= 3 × 4 – 26 + 14
= 12 – 26 + 14
= 26 – 26 = 0
∴ x = – 2 is a solution
Question 9.
What is the condition for an equation of the form ax2 + bx + c = 0 to become a linear equation.
Answer:
a = 0
Question 10.
Write the formula to find the nature of roots?
Answer:
discriminat = b2 – 4ac
Question 11.
Write the formula to form a Quadratic equation if their roots m and n are given.
Answer:
x2 – (m + n) x + mn = 0
III. Long Answer Questions:
Question 1.
Factorise \(\sqrt{2}\)x2 + 7x + 5\(\sqrt{2}\) = 0
Answer:

![]()
Question 2.
Factorize 0.2t2 – 0.04t = 0.03
Answer:
0.2t2 – 0.04t – 0.03 = 0
Multiply by 100
20t2 – 4t – 3 = 0
20t2 – 10t + 6t – 3 = 0
10t(2t- 1) + 3(2t – 1) = 0
(2t – 1) (10t + 3) = 0
(2t – 1) = 0 (or) (10t + 3) = 0
2t = 1 (or) 10t = – 3
t = \(\frac{1}{2}\) (or) t = \(\frac{-3}{10}\)
∴ \(\frac{1}{2}\) and \(\frac{-3}{10}\) are the roots of the equation.
Question 3.
Factorize a2 b2 x2 – (a2 + b2) x + 1 = 0
Answer:
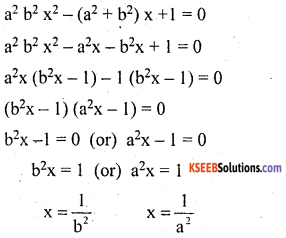
\(\frac{1}{a^{2}}\) & \(\frac{1}{b^{2}}\) are the roots of the equation.
Question 4.
Solve 2x2 + 5x – 3 = 0 by completing squares method.
Answer:

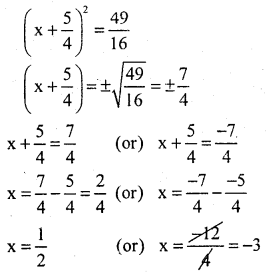
∴ \(\frac{1}{2}\) & – 3 and are the roots of the given equation.
![]()
Question 5.
Solve (2x + 3) (3x – 2) + 2 = 0 using formula.
Answer:
(2x + 3) (3x – 2) + 2 = 0
6x2 – 4x + 9x – 6 + 2 = 0
6x2 + 5x – 4 = 0
It is in the form of ax2 + bx + c = 0
a = 6, b = 5 and c = – 4

∴ \(\frac{-4}{3}\) and \(\frac{1}{2}\) are the roots of the given equation.
Question 6.
Solve a (x2 + 1) = x (a2 + 1) using formula.
Answer:
a(x2 + 1) = x (a2 + 1)
ax2 + a = x (a2) + 1
ax2 – (a2 + 1)x + a = 0
It is in the form of ax2 + bx + c = 0
a = a, b = – (a2 + 1) and c = a

x = \(\frac{2 a^{2}}{2 a}\) (or) x = \(\frac{2}{2 \mathrm{a}}\)
x = a (or) x = \(\frac{1}{a}\)
∴ a and \(\frac{1}{a}\) are the roots of the given equation.
Question 7.
For what Positive value of ‘m’ roots x2 – mx + 9 = 0 are
i. Equal
ii. distinct
iii. imaginary.
Answer:
x2 – mx + 9 = 0
It is in the form of ax2 + bx + c = 0
a = 1, b = – m and c = 9
∆ = b2 – 4ac
∆ = – (m)2 – 4 × 1 × 9
∆ = m2 – 36
i) If roots are equal
∆ = 0
m2 – 36 = 0
m2 = 36
m = \(\sqrt{36}\) = ±6
m = 6
ii) If roots are distinct
∆ > 0
m2 – 36 > 0
m2 > 36
m > ±6
∴ m > 6
iii) If roots are imaginary
∆ < 0
m2 – 36 < 0
m2 < 36
∴ m < ±6
∴ m < 6
Question 8.
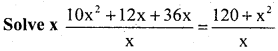
Answer:
10x2 + 12x + 36x – 120 – x2 = 0
9x2 + 36x – 108 = 0 divide by 9
x2 + 4x – 12 = 0
x2 + 6x – 2x – 12 = 0
(x + 6) – 2 (x + 6) = 0
(x + 6) (x – 2) = 0
x = – 6 (or) x = 2
![]()
Question 9.
Find the value of ‘P’ in a Quadratic equation (3P + 1) c2 + 2 (P + 1) c + P = 0 has equal roots.
Answer:
It is in the form of ax2 + bx + c = 0
a = (3P + 1) , b = 2(P + 1) and c = P
∆ = b2 – 4ac = 0 [has equal roots]
[2(P + 1)]2 – 4 × (3P + 1) P = 0
4(P2 + 2P + 1) – 4P(3P + 1) = 0
4[P2 + 2P + 1 – 3P2 – P] = 0
divide by 4
– 2P2 + P + 1 = 0 divide by – 1
2P2 – P – 1 = 0
2P2 – 2P + P – 1 = 0
2P(P – 1) + 1 (P – 1) = 0
(P – 1) (2P + 1) = 0
(P – 1) = 0 (or) 2P + 1 = 0
P = 1 (or) 2P = – 1
P = \(\frac{-1}{2}\)
∴ P = 1 (or) \(\frac{-1}{2}\)
Question 10.
In Rhombus ABCD the diagonals AC and BC intersect at E. If AE = x, BE = x + 7 and AB = x + 8. Find the lengths of the diagonals AC and BC.
Answer:
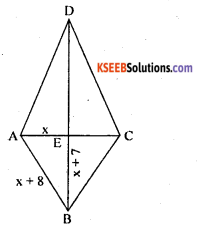
In Rhombus ABCD, AC and BD are diagonals are intersect at E.
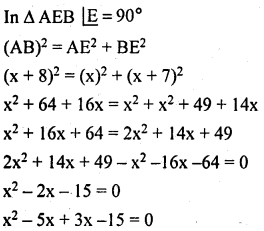
x (x – 5) + 3 ( x – 5) = 0
(x – 5) (x + 3) = 0
x – 5 = 0 & x + 3 = 0
x = 5 & x = – 3
AE = x = 5 cm
∴ AC = 5 + 5 = 10 cm
BE = x + 7 = 5 + 7 = 12 cm
BD= 12 + 12 = 24 cm
∴ two diagonals are 10 cm and 24 cm.
Question 11.
A motor boat whose speed is 15 km/hr in still water goes 30 km downstream and comes back in a total of 4 hours 30 minutes determine the speed of the stream.
Answer:
Let the speed of the stream be x km/hr
Speed of downstream = (15 + x) km/hr.
Time taken by the boat to go 30 km
downstream = \(\frac{30}{15+x}\) hours
Speed upstream = 15 – x hours
Time taken by the boat to go 30 km
Upstream = \(\frac{30}{15 – x}\) hrs
It is given that the boat returns to the same point in 4 hours 30 minutes.

The speed of the stream = 5 km/hr.
Question 12.
A dealer sells an article for ₹ 24 and gains as much percent as the cost price of the article. Find the cost price of the article.
Answer:
Let the C.P of the article = x
S.P = ₹ 24
Gain = x% of C.P

x2 = 2400 – 100x
x2 + 100x – 2400 = 0
x2 + 120x – 20x – 2400 = 0
x(x + 120) – 20(x + 120) = 0
(x + 120) (x – 20) = 0
x + 120 = 0 & x – 20 = 0
x = – 120 & x = 20
∴ The C.P of the article = ₹ 20
![]()