Students can Download Class 10 Maths Chapter 2 Triangles Additional Questions Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your in examinations
Karnataka State Syllabus Class 10 Maths Chapter 2 Triangles Additional Questions
I Multiple choice questions:
Question 1.
Two triangles are said to be similar if their corresponding sides are
a) Proportional
b) Equal
c) Paralled
d) Perpendicular
Answer:
a) Proportional
Question 2.
Congruent triangles are always,
a) Equal
b) similar
c) Not similar
d) Not equal
Answer:
a) Equal
Question 3.
Which of the following is can form similar triangles i) 3, 6, 9 ii) 9,18, 27 iii) 2,4, 6 iv) 5, 6, 7
a) i and ii
b) ii and iii
c) i and iii
d) i and iv
Answer:
a) i and ii
Question 4.
Basic proportional theorem is proposed by
a) Pythagoras
b) Thales
c) aryabhata
d) newton
Answer:
b) Thales
Question 5.
If straight line is drawn parallel to one side of a triangle then it divides the other two sides proportionally is called.
a) thales theorem
b) converse of thales theorem
c) Corollary of thales
d) Pythagoras theorem
Answer:
a) thales theorem
Question 6.
If straight-line divides two sides of a triangle proportionally then the straight line is parallel to the third side is called.
a) converse of thales theorem
b) pythogoral theorem
c) thales theorem
d) converse of Pythagoras theorem
Answer:
a) converse of thales theorem
Question 7.
In the given fig. which of following is
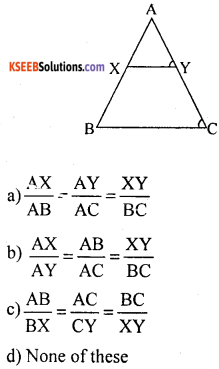
Answer:
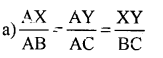
![]()
Question 8.
In the given fig. which of the following Is true
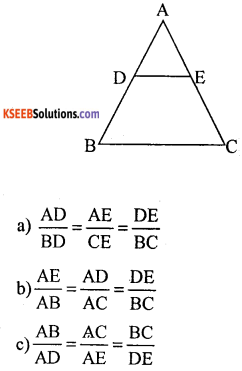
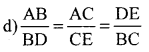
Answer:
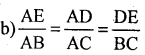
Question 9.
In the following figure DE || BC. AD = 4 cm, DB = 6 cm and AE =5 cm, then the value of EC is
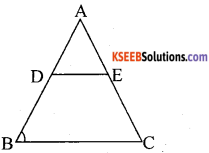
a) 6.5 cm
c) 7.5 cm
b) 7 cm
d) 8.0 cm
Answer:
c) 7.5 cm
Question 10.
In the following figure DE || BC then the value of ‘x’ is
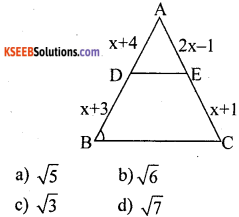
Answer:
![]()
Question 11.
In a trapezium the line joining the midpoints of non-parallel sides is.
a) Parallel to the parallel sides.
b) Half of the sum of the parallel side
c) both a and b
d) perpendicular to each other
Answer:
c) both a and b
Question 12.
If two triangles are equiangular then their corresponding sides are
a) proportional
b) equal
e) non-parallel
d) perpendicular
Answer:
a) proportional
Question 13.
If the three sides of a triangle are proportional to the corresponding three sides of another triangle then their corresponding angles are
a) equal
b) proportional
e) not equal
d) not proportional
Answer:
a) equal
Question 14.
In the given figure ∆ ADB ~ ∆ BDC then BD2 is
a) AD . AC
e) CD . AC
b) AD . CD
d) AB . BC
Answer:
b) AD . CD
![]()
Question 15.
In the given figure ∆ BDC ~ ∆ ABC then BC2 is
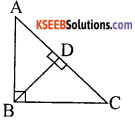
a) AC . CD
b) AC . AD
c) AD . CD
d) A13 . BC
Answer:
a) AC . CD
Question 16.
In the given figure ∆ ADB ~ ∆ BDC then B2 is
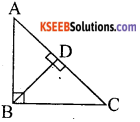
a) AC . AD
c) AD . CD
b) AC . CD
d) AB . BC
Answer:
a) AC . AD
Question 17.
If the area of two similar triangles are equal then they are
a) similar
b) congruent
e) proportional
d) equal
Answer:
d) equal
Question 18.
Area of similar triangles are proportional to
a) squares on their corresponding sides
b) squares on their corresponding altitude
e) squares on their corresponding medians
d) all the above
Answer:
d) all the above
Question 19.
The corresponding altitudes of two similar triangles are 9 cm and 15cm respectively then the ratio between their areas.
a) 9 : 15
b) 100 : 25
c) 81 : 225
d) 3 : 15
Answer:
c) 81 : 225
Question 20.
In a trapezium ABCD AB || CD and Its diagonals intersect at 0. if AB = 6 cm and DC = 3 cm then the ratio of the area of AOB and COD
a) 4 : 1
b) 1 : 2
c) 2 : 1
d) 1 : 4
Answer:
a) 4 : 1
II. Short Answer Questions:
Question 1.
State thales theorem (Basic proportionality theorem).
Answer:
A straight drawn parallel to one side of triangle then other two sides divides proportionally.
Question 2.
State converse of thales theorem.
Answer:
If two sides divides proportionally then straight line drawn parallel to given side.
Question 3.
What is the ratio of areas of two similar triangles whose sides are in the ratio 3 : 4
Answer:

∴ Ratio of areas are 9 : 16
Question 4.
If two triangles are similar such that the ratio of their areas 36 : 121, then what is the ratio of their corresponding medians.
Answer:
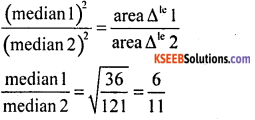
∴ ratio of their corresponding medians 6 : 11
![]()
Question 5.
Is the triangle with sides 12 cm, 16 cm and 18 cm a right triangle? give reason.
Answer:
122 + 162 = 182
144 + 256 = 324
400 ≠ 324
LHS ≠ RHS
∴ Given sides not form right angle ∆le.
Question 6.
What is the name given to the longest side of a right-angled triangle
Answer:
hypotenuse
Question 7.
State pythagoras theorem
Answer:
In a right-angled triangle square on the hypotenuse is equal to sum of the squares of other sides.
Question 8.
State converse of pythagoras theorem.
Answer:
“If the square on the longest side of a triangle is equal to the sum of the squares on the other two sides, then those two sides contain a right angle”.
Question 9.
Verify m2 – n2, 2mn, m2 + n2 form the sides of a right-angled triangle.
Answer:
(m2 + n2)2 = (m2 – n2)2 + (2mn)2
m4 + 2m2n2 + n4 = m4 – 2m2n2 + n4 + 4m2n2
m4 + n4 + 2m2n2 m – n4 + 2m2n2
LHS = RHS
given sides form right angle ∆le.
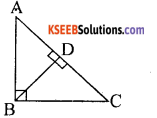
Question 10.
In figure ∠ABC = 90°, BD ⊥ AC if BD = 8 cm, AD = 4 cm, find CD
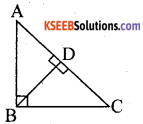
Answer:
BD2 = AD × CD
(8)2 = 4 × CD
64 = 4 CD
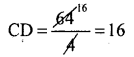
III. Long answer questions:
Question 1.
In Fig. \(\frac{A O}{O C}=\frac{B O}{O D}=\frac{1}{2}\) and AB = 5 cm. Find the value of DC.
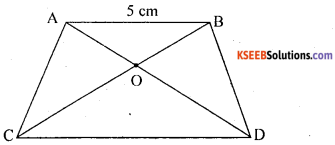
Answer:

Question 2.
ABC is an equilateral triangle of side 4a. Find each of its altitude.
Answer:
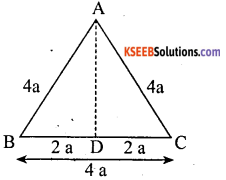
Let ABC be an equilateral triangle of side 4a units, We draw AD ⊥ BC. Then D is the mid-point of BC.
![]()
Now ABD is a right ∆le right angle at D.
∴ AB2 = AD2 + (2a)2. [By Pythagoras theorem]
= (4a)2 = AD2 + 4a2
= AD2 = 16a2 – 4a2 = 12a2
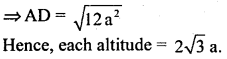
![]()
Question 3.
If the diagonals of a quadrilateral divide each other proportionally prove that is a trapezium?
Answer:

Question 4.
ABC is a triangle in which AB = AC and D is a point on AC such that BC2 = AC × CD Prove that BD = BC.
Answer:
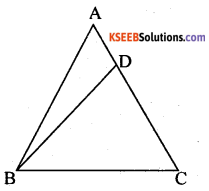
Given: ∆ ABC in which AB = AC and D is a point on the side AC such that BC2 = AC x CD.
To prove: BD = BC
Construction: Join BD
Proof: We have,

Question 5.
A door of width 6 meter has an arc above it having a height of 2 meters find the radius of the arc?
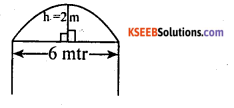
Answer:
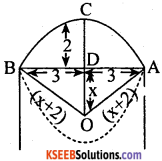
![]()
Let the radius of the semi – circle
OA = OC = OB
= (x + 2)m
=> OA = OB. In ∆ OAB
∆ OAB is an isosceles ∆le
∴ OD ⊥ AB.
=> OD bisects AB
∴ AD = BD = 3 cm.
In ∆le OAD, ∠PDA = 90°
AO2 = AD2 + OD2
(x+2)2 = 32 + x2
x2 + 4x + 4 = 9 + x2
4x = 9 – 4 = 5
x = \(\frac{5}{4}\)
Hence, radius = x + 2
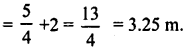
Question 6.
In an equilateral ∆le ABC, AD is drawn ⊥r to BC meeting BC in D, prove that AD2 = 3BD2.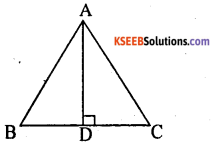
Answer:
In ∆ ABD, ∠ADB = 90°
Then by pythagoras theorem
=> AB2 = AD2 + BD2
=> BC2 = AD2 + BD2, [BC = 2BD]
∴ AB = BC = CA
=> (2BD)2 = AD2 + BD2
∴ (⊥ is the median in an equilateral ∆le)
3BD2 = AD2.
![]()
Question 7.
In the given figure, AD ⊥ BC and BD = \(\frac{1}{3}\) CD prove that 2AC2 = 2AB2 + BC2.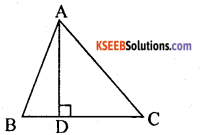
Answer:
In right ∆ ABD, by pythogoras theorem.
∴ AB2 = AD2 + BD2
In right ∆ ABC, by pythagoras theorem.
∴ AC2 = AD2 + DC2
Subtracting (ii) from (i) we get,
∴ AB2 – AC2 = BD2 – DC2

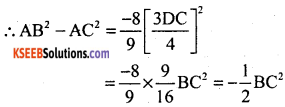
Question 8.
Triangle ABC is right angles at B and D is the mid-point of BC? Prove that AC2 = 4AD2 – 3AB2.
Answer:
Given: ABC is right angled at B and D is the mid-point of B C
BD = DC = \(\frac{1}{2}\) BC
In ∆ ABD, AD2 = AB2 + BD2
[pythogoras theorem] – (1)
In ∆ ABC, AC2 = AB2 + BC2
[pythogoras theorem] – (2)
From eqn (1) and (2)
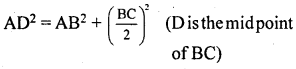
=> 4AD2 = 4AB2 + BC2
=> BC2 = 4AD2 – 4AB2 – (3)
Using this eqn in (2)
AC2 = AB2 + 4AD2 – 4AB2
AC2 = 4AD2 – 3AB2.
Question 9.
Through the midpoint M of the sides of parallelogram ABCD. The line BM is drawn intersecting AC at L and AD produced to E. Prove that EL = 2BL.
Answer:

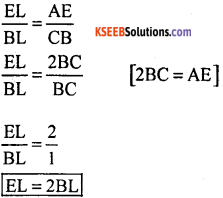
Question 10.
Prove that any two medians of a ∆le divide each other in the ratio 2:1.
Answer:
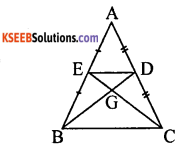
In ∆le ABC, BD, CE are two medians intersecting at G.
∴ AE = EB, AD = DC [medians divides equally]

Question 11.
A ladder of length 2.6 m is lended against a wall. When it is at a distance of 2.4 m from the foot of the wall, the top of the ladder touches the bottom edge of the window in the wall, if the foot of the ladder is moved 1.4 m towards the wall it touches the top edge of the window, find the height of the window.
Answer:
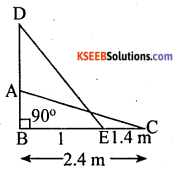
Length of ladder AC = DE = 2.6 m
Height of window AD =?
BC = 2.4 m
EC = 1.4 m
BE = 1 m
In ∆le ABC
AC2 = AB2 + BC2
AB2 = AC2 – BC2
AB2 = (2.6)2 – (2.4)2
= (2.6 + 2.4) x (2.6 – 2.4)
= 5 x 0.2 = lm
AB = 1m
In ∆le DBE
DE2 = BD2 + BE2
(2.6)2 – 12 = BD2
BD2 = (2.6 + 1) (2.6 – 1)
= 3.6 x 1.6
BD = ![]()
BD = 2.4 m
∴ Height of window
AD = BD – AB
= 2.4 – 1 = 1.4
Height of window = 1.4m
![]()
Question 12.
In a ∆le ABC, D and E be two points on side AB such that AD = BE : IF DE || BC and EQ || AC, then prove that PQ || AB.
Answer:
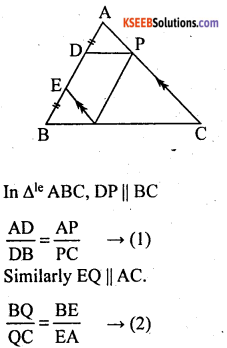
From fig, given BE = AD
EA = AD + DE
= BE + ED
= BD
Then (2) becomes

∴ PQ || AB [converse of BPT]
Question 13.
A tree 32 m tall broke due to gale and Its top fell at a distance of 16m from its foot at what height above the ground did the tree break?
Answer:
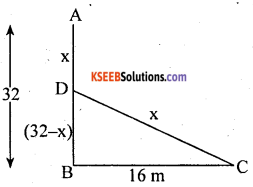
Height of the tree AB = 32 m
AD is broken part of tree = x
BC is distance between foot to the top oftreeBC = 16m
BD is the remaining height of tree = 32 – x
In Ale BDC ∠B = 90°
(CD)2 = BD2 + BC2
x2 = (32 -x)2 + (16)2
x2 = 1024 + x2 – 64x + 256
x2 – x2 = 1280 – 64x
64x = 1280
x = \(\frac{1280}{64}\)
x = 20m
Remaining part of a tree
BD = (32 – x) = 32 – 20 = 12m
Question 14.
In ∆le ABC, i) ∠ACB = 60°, ii) AD ⊥ar BC. Derive an expression for AB in terms of AC and BC.
Answer:
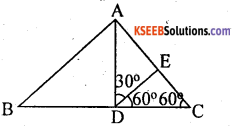
In ∆le ABC
i) ∠ACB = 60° and
ii) AD ⊥r BC
Construction:
Draw DE such that ∠EDC = 60°
∴ Ale DEC is an equilateral
(Data and construction)
DE = DC = EC
Ale DEA is an isosceles Ale [∴ AED = 120 and ∠ ADE = 30° = ∠ DAE]
DE = EA
=> DC = EA = EC [∴ Axiom – 1]
∴ AC = 2DC
Now in Ale ADB, AB2 = AD2 + BD2 [pythagoras theorem]
AB2 = (AC2 – DC2) + (BC -CD)2
AB2 = 4DC2 – DC2 + BC2 – 2BC DC + DC2 [∴ AC = 2DC]
AB2 = 4DC2 + BC2 – 2BC . DC
AB2 = 4DC2 – 2BC . DC + BC2
AB2 = 2DC (2DC – BC) + BC2
= AC (AC – BC) + BC2 [2DC = AC]
AB2 = AC2 – AC . BC + BC2
AB2 = AC2 + BC2 – AC.BC
Question 15.
ABCD is a rhombus. Prove that AC2 + BD2 = 4AB2
Answer:
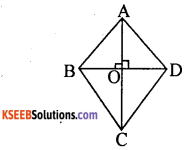
Given: In rhombus ABCD, AC and BD are diagonals, AB = BC = CD = DA
∴ AO = 1/2 AC and BO = 1/2 BD
To prove: AC2 + BD2 = 4AB2
In right angle ∆le AOB, ∠O = 90°
AB2 = OA2 + OB2
AB2 = (1/2 AC)2 + (1/2 BD)2
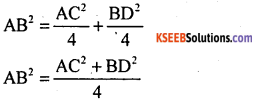
4AB2 = AC2 + BD2
Question 16.
AD is the altitude from A to BC in the ∆ ABC and DB:CD = 3:1 prove that BC2 = 2(AB2 – AC2)
Answer:
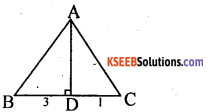
In ∆le ABD ∠D = 90°
AB2 = AD2 + BD2
AD2 = AB2 – BD2 – (1)
In ∆le ADC ∠D = 90°
AC2 = AD2 + CD2
AD2 = AC2 – CD2 – (2)
From (1) and (2)
AB2 – BD2 = AC2 – CD2
AB2 – AC2 = BD2 – CD2
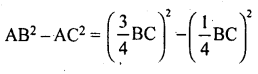
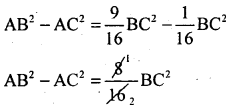
BC2 = 2(AB2 – AC2)
![]()
Question 17.
In the given figure in ∆ ABC, AD ⊥ BC and AD2 = BD × CD. Prove that the ∆ ABC is a right angle triangle.
Answer:
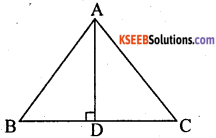
∆ ABC, AD ⊥ BC and AD2 = BD × CD
To prove: ∆ ABC is a right angle triangle
Proof: In ∆le ABD ∠D = 90°
AB2 = BD2 + AD2 – (1)
In ∆le ADC ∠D = 90°
AC2 = AD2 + DC2 – (2)
Adding eqn (1) and (2)
AB2 + AC2 = BD2 + AD2 + AD2 + DC2
= 2 AD2 + BD2 + DC2
= 2(BD x CD) + BD2 + DC2
= (BD + DC)2
∴ AB2 + AC2 = BC2
∆ ABC is a right triangle, right angled at A.
Question 18.
In trapezium ABCD, AB || CD and DC = 2AB. EF || AB, where E and F lie on BC and AD respectively such \(\frac{B E}{E C}=\frac{4}{3}\) . Diagonal BD intersect EF at G. Prove that 7EF = 11 AB.
Answer:
In trapezium ABCD, AB || CD and



Question 19.
A peacock on a pillar of 9 feet height on seeing a snake coming towards is hole situated just below the pillar from a distance 27 feet away from the pillar will fly to catch it. If both possess the same speed, how far from the pillar they are going to meet?
Answer:
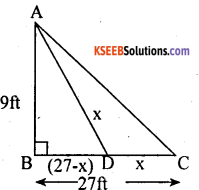
AB is the height of pillar = 9ft
BC is the distance b/w pillar and the snake hole = 27 ft
AD = CD = x ft
BD = 27 – x
In ∆ ABD ∠D = 90°
AD2 = AB2 + BD2 [By pythagoras theorem]
(x)2 = (9)2 + (27 – x)2
x2 = 81 + 729 + x2 – 54x
54x = 810
x = \(\frac{810}{54}\)
x = 15 ft
BD = 27 – x = 27 – 15 = 12 ft
∴ Both of these going to meet at a distance. 12ft from the pillar.
Question 20.
In ∆ MGN, MP ⊥ GN. If MG = a units, MN = b units, GP = c units and PN = d unit. Prove that (a + b) (a – b) = (c + d) (c – d).
Answer:
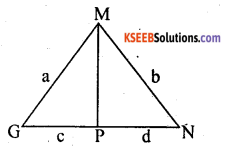
In ∆le MGP ∠P = 90°
MG2 = GP2 + MP2
(a)2 = (c)2 + MP2
MP2 = a2 – c2 – (1)
In ∆le MNP ∠P = 90°
MN2 = PM2 + PN2
(b)2 = d2 + MP2
MP2 = b2 – d2 – (2)
From (1) and (2)
a2 – c2 = b2 – d2
a2 – b2 = c2 – d2
(a + b) (a – b) = (c + d) (c – d).
![]()