Students can Download Class 10 Maths Chapter 8 Real Numbers Additional Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 10 Maths Chapter 8 Real Numbers Additional Questions
I. Multiple Choice Questions:
Question 1.
The H.C.F of 2 and 3 by Euclid’s division lemma
a. 2
b. 3
c. 5
d. 1
Answer:
d. 1
![]()
Question 2.
The H.C.F of 10 and 5 is
a. 5
b. 10
c. 15
d. 150
Answer:
a. 5
Question 3.
The relation of Euclid’s division lemma is
a. a = bq + r
b. a = b + q × r
c. a = bqr
d. a = (b – q) r
Answer:
a. a = bq + r
Question 4.
Which of the fololwing is a rational number.
a. \(\sqrt{2}\)
b. π
c. \(\frac{1}{3}\)
d. \(\sqrt{3}\)
Answer:
c. \(\frac{1}{3}\)
Question 5.
What are the quotient and remainder when 10 is divided by 3
a. 3, 1
b. 1, 3
c. 1, 1
d. 3, 3
Answer:
a. 3, 1
Question 6.
What is the H.C.F of two consecutive natural numbers?
a. 1
b. 2
c. 3
d. 4
Answer:
a. 1
Question 7.
The prime factors of 256 is
a. 26
b. 27
c. 28
d. 29
Answer:
c. 28
Question 8.
If a and b are two positive integers then H.C.F (a.b) × L.C.M (a, b) =
a. a + b
b. a × b
c. a2 + b2
d. 2ab
Answer:
b. a × b
![]()
Question 9.
\(\sqrt{2}\) is
a. a rational number
b. an irrational number
c. an integer
d. a natural number
Answer:
b. an irrational number
Question 10.
5 – \(\sqrt{3}\) is
a. an irrational number
b. a rational number
c. a composite number
d. a prime number
Answer:
a. an irrational number
Question 11.
Which of the following is not an irrational number?
a. \(\sqrt{2}\)
b. \(\sqrt{3}\)
c. \(\sqrt{9}\)
d. \(\sqrt{5}\)
Answer:
c. \(\sqrt{9}\)
Question 12.
The number of prime number between 1 and 10 is
a. 2
b. 3
c. 4
d. 12
Answer:
c. 4
Question 13.
π is
a. an irrational number
b. a rational number
c. a prime number
d. a composite number
Answer:
a. an irrational number
Question 14.
H.C.F (8, 9, 25) × L.C.M (8, 9, 25)
a. 1800
b. 2.25
c. 2.375
d. 3600
Answer:
a. 1800
Question 15.
The decimal expansion of \(\frac{17}{8}\) is
a. 2.1
b. 2.25
c. 2.375
d. 2.0125
Answer:
a. 2.1
II. Short Answer Questions:
Question 1.
What is the use of Euclid’s division lemma?
Answer:
Euclid’s division lemma can be used only for calculating H.C.F.
![]()
Question 2.
Write the even prime number.
Answer:
2.
Question 3.
(7 × 11 × 13 + 13) is a composite number. Justify the statement.
Answer:
(7 × 11 × 13) + 13
= 13(77 + 1) =13 × 78.
∴ 78 is composite number.
∴ It is a composite number.
Question 4.
What is the HCF of 33× 5 and 32 × 52
Answer:
HCF of 33 × 5 and 32 × 52
= 32 × 5 = 45
Question 5.
Find the value of ‘a’ in the factor tree.
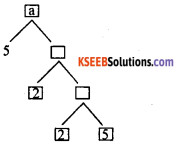
Answer:
2 × 5 = 10
10 × 2 = 20
20 × 5 = 100
∴ a= 100
Question 6.
Given that L.C.M (91, 26) = 182, then Find H.C.F (91,26)
Answer:
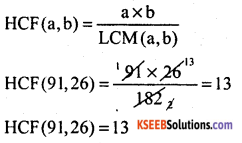
Question 7.
What the two numbers called if their HCF is 1.
Answer:
Co-Prime numbers
Question 8.
If P is prime number then, what is the LCM of P, P2 and P5.
Answer:
P5.
Question 9.
Define twin prime numbers.
Answer:
A pair of prime numbers is said to be twin primes it they differ by 2. Eg: (3,5) & (11,13)
![]()
Question 10.
Write the prime factors of 210.
Answer:
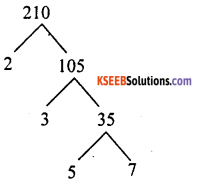
210 = 2 × 3 × 5 × 7
III. Long Answer Questions:
Question 1.
If n is odd positive integer. Show that (n5 – 1) divisible by 8?
Answer:
We know that an odd positive integer n is of the form (4q + 1) or (4q + 3) for some integer q.
Case – I
when n = (4q + 1)
In case n2 – 1 = (4q + 1)2 – 1
= 162 q2 + 8q = 8q(2q + 1)
which is clearly divisible by 8.
Case – II
When n = (4q + 3)
In this case, we have.
n2 – 1 = (4q + 3)2 – 1
= 16 q2 + 24q + 8(2q2 + 3q + 1)
which is clearly divisible by 8.
Hence (n2 – 1) is divisible by 8.
Question 2.
Using prime factorisation method, find the HCF and LCM of 30, 72 and 432. Also show that HCF × LCM ≠ product of three no. ?
Answer:
Given Numbers = 30, 72, 432.
30 = 2 × 3 × 5; 72 = 23 × 32 and 432 = 24 × 32
Here 21 and 31 are the smallest powers of the common factors 2 and 3 respectively.
So, HCF (30, 72, 432) = 21 × 31
= 2 × 3 = 6.
Again 24, 33 and 51 are the greatest powers of the prime factors 2, 3 and 5 respectively.
So, LCM (30, 72, 432)
= 24 × 33 × 51 = 2160
HCF × LCM = 6 × 2160 = 12960
Product of numbers = 30 × 72 × 432 = 933120
∴ HCF × LCM ≠ product of the number.
![]()
Question 3.
Find the largest positive integer that will divide 398, 436 and 542 leaving remainders 7, 11 and 15 respectively.
Answer:
It is given on dividing 398 by the required number, that is a remainder of 7. This means that 398 – 7 = 391 is exactly divisible by the required number. In other words, required number is a factor of 391.
Similarly, required positive integer is a factor of (436 – 11= 425) and (542 – 15 = 527). Clearly, required number is the HCF of 391, 425 and 527.
Using the factors tree, we get the prime factorisations of 391, 425 and 527 as follows. 391 = 17 × 23, 425 = 52 × 17 and 527 = 17 × 31
∴ HCF of 391, 425 and 527 is 17
Hence, required number = 17
Question 4.
There are 75 roses and 45 lily flowers. These are to be made into bouquets containing both the flowers. All the bouquets should contain the same number of flowers. Find the number of bouquets that can be formed and the number of flowers in them?
Answer:
The number of bouquets = HCF of (75, 45). Now by Euclid’s algorithm from 75 and 45

HCF of 75 and 45 is 15
Each bouquets contains = 15 flowers
∴ Number of roses in bouquets = \(\frac{75}{15}\) = 5
∴ Number of lilly’s in bouquets = \(\frac{45}{15}\) = 3
∴ Number of bouquets = 8
Question 5.
In a school, the strength in 8th, 9th and 10th standards are respectively 48, 42 and 60. Find the least number of books required to be distributed equally among the students of 8th, 9th and 10th standard?
Answer:
The least number of books required.
= LCM(48, 42 and 60)
Now 48 = 2 × 2 × 2 × 2 × 3 =24 × 3
42 = 2 × 3 × 7
60 = 2 × 2 × 3 × 5
Hence LCM (48, 42 and 60)
= 24 × 3 × 7 × 5 = 1680.
∴ Number of books required is 1680.
Question 6.
Show that any positive odd integers is of the form 4q + 1 or 4q + 3, where q is some integer.
Answer:
By Euclid’s division algorithm,
a + bq + r
Take b = 4 ∴ r = 0, 1, 2, 3
So, a = 4q, 4q + 1, 4q + 2, 4q + 3
Clearly a = 4q ; 4q + 2 are even, as they are divisible by 2.
But 4q + 1, 4q + 3 are odd, as they are not divisible by 2.
∴ Any positive odd integer is of the form (4q + 1) or (4q + 3)
![]()
Question 7.
x, y and z start at the same time in the same direction to run around a circular stadium x completes a round in 126 sec y in 154 sec and z in 231 sec all starting at the same point. After what time will they meet again at the starting point. How many rounds would have x, y and z completed by this time?
Answer:
To find LCM(126, 154, 231)
126 = 2 × 3 × 3 × 7
154 = 2 × 7 × 11
231 = 3 × 7 × 11
LCM of 126, 154, 231.
= 2 × 3 × 3 × 7 × 11
= 1386,
Hence, after 1386 sec they meet again the starting point.
Now x completed the rounds = \(\frac{1386}{126}\)
= 11 rounds
Y completed the rounds = \(\frac{1386}{154}\)
= 9 rounds
z completed the rounds = \(\frac{1386}{231}\)
= 6 rounds
Question 8.
Show that any positive even integers of the form 4q or 4q + 2, where is q is a whole number.
Ans:
(a) Let ‘a’ be an even positive integer,
a = 4q + r
a = 4q + r, where 0 ≤ r ≤ 4
a = 2 (2q) + r where r = 0, 1, 2, 3
Since a is an even positive integer, 2
divides ‘a’ ∴ r = 0
a = 2(2q) + 0
a = 4q.
(b) Let ‘a’ be an in even positive integer
Apply division algorithm with ‘a’ and ‘b’ where b = 4.
a = 4q + r where 0 ≤ r < 4
a = 4q + 2 = 2(2q) + 2
= 2(2q + 1).
Since ‘a’ is an even positive integer, 2 divides ‘a’
r = 2.
a = 2(2q + 1)
a = 4q + 2
Hence a = 4q + 2, when ‘a’ is an even positive integer.
Question 9.
The HCF of 65 and 117 is expressible in the form 65m – 117, find the value of m. Also find the LCM of 65 and 117 using prime factorisation method?
Answer:
We have 117 = 65 × 1 + 52
65 = 52 × 1 + 13
52 = 13 × 4 + 0
Hence HCF (65, 117) = 13
∴ 65m – 117 = HCF = 13
⇒ 65m = 117 + 13 = 130.
m = \(\frac{130}{65}\) = 2
Now = 65 = 13 × 5
117 = 32 × 13
LCM (65, 117) = 113 × 5 × 32
= 585.
Question 10.
The length and breadth of a rectangular field is 110m and 30m respectively. Calculate the length of the longest rod which can measure the length and breadth of field exactly.
Answer:
Length = 110 m; Breadth = 30 m.
We have to find HCF of 110 and 30 by Euclid’s Lemma.
110 = (30 × 3) + 20
30 = (20 × 1) + 10; 20 = (10 × 2) + 0
HCF of 110 and 30 is 10.
∴ Length of longest rod is 10 m.
Question 11.
Prove that \(\frac{\sqrt{7}}{5}\) is an irrational number.
Answer:

But \(\sqrt{7}\) is not a rational number. This leads us to a contradiction.
Our as supposition that \(\frac{\sqrt{7}}{4}\) number is wrong.
⇒ \(\frac{\sqrt{7}}{4}\) is a rational number.
![]()