Students can Download Class 10 Maths Chapter 9 Polynomials Additional Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 10 Maths Chapter 9 Polynomials Additional Questions
I. Multiple Choice Questions:
Question 1.
The degree of polynomial is x + 2
a. 2
b. 1
c. 3
d. 4
Answer:
b. 1
![]()
Question 2.
The degree of a quadratic polynomial is
a. 0
b. 1
c. 2
d. 3
Answer:
c. 2
Question 3.
The degree polynomial of a bi-quadratic
a. 0
b. 2
c. 4
d. 1
Answer:
c. 4
Question 4.
The standard polynomial. form of a linear
a. ax + c
b. ax2 + c
c. ax2 + bx + c = 0
d. ax3 + bx2 + cx + d = 0
Answer:
a. ax + c
Question 5.
The standard form of a quadratic equation.
a. ax2 + bx + c = 0
b. ax + c = 0
c. ax2 + c = 0
d. ax3 + bx + c = 0
Answer:
a. ax2 + bx + c = 0
Question 6.
A polynomial of degree 3 is called
a. a linear polynomial
b. a quadratic polynomial
c. a cubic polynomial
d. a biquadratic polynomial
Answer:
c. a cubic polynomial
![]()
Question 7.
The value of px. = x2 – 3x – 4, x = -1
a. 1
b. – 4
c. 0
d. – 3
Answer:
c. 0
Question 8.
The degree of the polynomial x4 + x3 is
a. 2
b. 3
c. 5
d. 4
Answer:
d. 4
Question 9.
The number of zeroes of linear polynomial at most is
a. 0
b. 1
c. 2
d. 3
Answer:
b. 1
Question 10.
The degree of polynomial x + 2. x + 1. is
a. 1
b. 3
c. 4
d. 2
Answer:
d. 2
Question 11.
The degree of a zero polynomial is
a. not defined
b. 1
c. 2
d. 3
Answer:
a. not defined
Question 12.
The zeroes of the polynomial x3 -4x are
a. 0, ± 2
b. 0, ± 1
c. 0, ± 3
d. 0, 0
Answer:
a. 0, ± 2
Question 13.
The zeroes of the polynomials, t2 – 15 are.
a. ± \(\sqrt{15}\)
b. ± \(\sqrt{5}\)
c. ± \(\sqrt{3}\)
d. ± 3
Answer:
a. ± \(\sqrt{15}\)
![]()
Question 14.
Dividend is equal to.
a. divisor × quotient + remainder
b. divisor × quotient
c. divisor × quotient – remainder
d. divisor × quotient × remainder
Answer:
a. divisor × quotient + remainder
Question 15.
If the divisor is x2 and quotient is x while the number remainder is 1, then the dividend is.
a. x2
b. x
c. x3
d. x3 + 1
Answer:
d. x3 + 1
Question 16.
What is the co-efficient of the first term of the quotient when 2x2 + 2x + 1 is divided by x + 2?
a. 1
b. 2
c. 3
d. – 2
Answer:
b. 2
Question 17.
The zeroes of the polynomial x2 – 3x – 4 are
a. 4, – 1
b. 4, 1
c. – 4, 1
d.- 4, – 1
Answer:
a. 4, – 1
Question 18.
If f(x) = x2 – 1 the value of f(2) is
a. 1
b. 3
c. 4
d. 0
Answer:
b. 3
Question 19.
If f(x) = 8 f(x) is called
a. Constant polynomials
b. linear polynomials
c. quadratic polynomials
d. Cubic polynomials
Answer:
a. Constant polynomials
![]()
Question 20.
A cubic polynomial has at most
a. 1 zeroes
b. 2 zeroes
c. 3 zeroes
d. 4 zeroes.
Answer:
c. 3 zeroes
II. Short Answer Questions:
Question 1.
Find the value of P(x) = x2 + 2x – 5 at x = 1
Answer:
P(x) = x2 + 2x – 5
P (1) = (1)2 + 2(1) – 5 = 1 + 2 – 5
= 3 – 5
P(1) = – 2
Question 2.
If x = 1 is a zero of the Polynomial f(x) = x3 – 2x2 + 4x + K, write the value of K.
Answer:
f(x) = x3 – 2x2 + 4x + K x = 1
f(1) = (1)3 – 2(1)2 + 4(1) + K
f(1) = 0 zero of the polynomial
0 = 1 – 2 + 4 + K
0 = 3 + K
K = – 3
Question 3.
If α and β are zeroes of Polynomials P(x) = x2 – 5x + 6, then find the value of α + β – 3αβ.
Answer:
α + β = \(\frac{-b}{a}=\frac{-(-5)}{1}\) = 5 and
αβ = \(\frac{c}{a}=\frac{6}{1}\) = 6
α + β – 3αβ
= 5 – 3(6)
= 5 – 18 = -13
α + β – 3αβ = – 13
![]()
Question 4.
Find the zeroes of the Polynomial P(x) = 4x2 – 12x + 9
Answer:
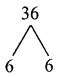
P(x) = 4x2 – 12x + 9
4x2 – 6x – 6x + 9 = 0
2x(2x – 3) – 3(2x – 3) = 0
(2x – 3) (2x – 3) = 0
x = \(\frac{3}{2}\), \(\frac{3}{2}\)
Question 5.
If 1 is a zero of the Polynomial P(x) = ax2 – 3(a – 1) x – 1, then find the value of a.
Answer:
P(x) = ax2 – 3(a – 1) x – 1
∴ x = 1
P(1) = a(1)2 – 3(a – 1) 1 – 1
P(1) = a – 3a + 3 – 1
0 = – 2a + 2
2a = 2
a = \(\frac{2}{2}\) = 1
a = 1
Question 6.
Write the degree of the Polynomial 3x3 – x4 + 5x + 3
Answer:
3x3 – x4 + 5x + 3
– x4 + 3x3 + 5x + 3
∴ degree of the Polynomial is 4
Question 7.
Write the standard form of a cubic Polynomial.
Answer:
ax3 + bx3 + cx + d.
Question 8.
Find the zero of the Polynomial , P(x) = a2x, a ≠ 0
Answer:
P(x) = a2x
a2x = 0
x = \(\frac{0}{a^{2}}\)
x = 0
Question 9.
If α and β are the zeroes of the polynomial 4x2 + 3x + 7, then find the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:

III. Long Answer Questions:
Question 1.
Find the zeroes of the following quadratic polynomials x2 + 4x + 4.
Answer:
f(x) = x2 + 4x + 4
0 = x2 + 2x + 2x + 4
0 = x(x + 2) + 2(x + 2)
(x + 2) (or) (x + 2) = 0
x + 2 = 0 (or) x + 2 = 0
x = – 2 x = – 2.
Zeroes of the Polynomials x2 + 4x + 4 are – 2 and – 2
![]()
Question 2.
If x = 1 is a zero of the polynomial f(x) = x3 – 2x2 + 4x + K, find the value of K.
Answer:
f(x) = x3 – 2x2 + 4x + K
∴ x = 1
f(x) = (1)3 – 2(1)2 + 4(1) + K
0 = 1 – 2(1) + 4 + K [f(1) = 0]
0 = 1 – 2 + 4 + K.
K + 3 = 0
K = – 3
Question 3.
For what value of K, – 4 is a zero of the polynomial x2 – x – (2K + 2)?
Answer:
f(x) = x2 – x – (2K + 2) and f(x) = 0
x = – 4
f(- 4) = (- 4)2 (- 4) – (2K + 2)
0 = 16 + 4 – 2K – 2
20 – 2 – 2K = 0 ⇒ 18 = 2K
K = \(\frac{18}{2}\) ⇒ K = 9
Question 4.
Divide p(x) by g(x) in each of the following cases and verify division algorithm.
P(x) = x2 + 4x + 4, g(x) = x + 2
Answer:
x2 + 4x + 4 ÷ x + 2
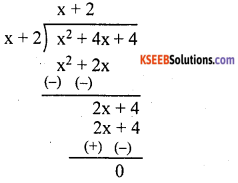
q(x) = x + 2 and r(x) = 0
Question 5.
On dividing the polynomial. P(x) = x3 – 3x2 + x + 2 by a polynomial g(x) the quotient and remainder were (x – 2) and (- 2x + 4) respectively. Find g(x).
Answer:
P(x) = x3 – 3x2 + x + 2
q(x) = (x – 2); r(x) = (- 2x + 4)
g(x) = ?
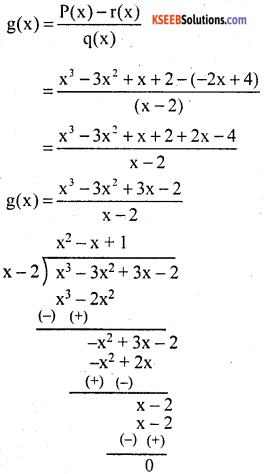
g(x) = x2 – x + 1; r(x) = 0
∴ The divisor is x2 – x + 1
![]()
Question 6.
What must be subtracted from x3 + 5x2 + 5x + 8 so that the resulting polynomial is exactly divisible by x2 + 3x – 2?
Answer:
P(x) = x3 + 5x2 + 5x + 8
g(x) = x2 + 3x – 2
P(x) = g(x) q(x) + r(x)

q(x) = x + 2; r(x) = x + 12
If we subtract x + 12 from x3 + 5x2 + 5x + 8 it will be exactly divisible by x2 + 3x – 2
Question 7.
What should be added to (x4 – 1) so that it’ is exactly divisible by (x2 + 2x + 1)?
Answer:
P(x) = x4 – 1 g(x) = x2 + 2x + 1
x4 + 0x3 + 0x3 + 0x – 1

r(x) = – 4x – 4
– {r(x)} = {4x + 4}
Question 8.
If the polynomials 2x3 + ax2 + 3x – 5 and x3 + x2 – 4x – a leave the same remainder when divided by x – 1 find the value of a.
Answer:
x – 1 = 0 [∴ g(x) = (0)]
x = 1
P(x) = 2x3 + ax2 + 3x – 5
P(1) = 2(1)3 + a(1)3 + 3(1) – 5
P(1) = 2 + a + 3 – 5
P(1) = a ➝ (1)
g(x) = x3 + x2 – 4x – a
g(1) = (1)3 + (1)2 – 4(1) – a
= 1 + 1 – 4 – a
g(x) = – 2 – a ➝ (2)
g(1) = g(1) [∴ Polynomials are leave same remainder]
a = – 2 – a
a + a = – 2
2a = – 2
a = \(\frac{-2}{2}\)
a = – 1
Question 9.
If (x3 + ax2 – bx + 10) is divisible by x3 – 3x + 2, find the values of a and b.
Answer:
P(x) = x3 + ax2 – bx + 10
g(x) = x2 – 3x + 2
x2 – 2x – x + 2 = 0
x(x – 2) – 1(x – 2) = 0
(x – 2) (x – 1) = 0
x = 2 and x = 1
P(x) = x3 + ax2 – bx + 10
P(x) = (1)3 + a(1)2 – b(1) + 10
= 1 + a – b + 10
0 = a – b + 11
a – b = – 11 ➝ (1)
P(2) = (2)3 + a(2)2 – b(2) + 10
P(2) = 8 + 4a – 2b – 10
0 = 4a – 2b + 18
4a – 2b = – 18 ➝ (2)
Multiply equation (1) by 4 and subtract with equation (2)
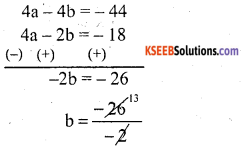
b = 13
Put b = 13 in equation (1)
a – b = – 11
a – 13 = – 11
a = – 11 + 13
a = 2
![]()
Question 10.
If both x – 2 and x – \(\frac{1}{2}\) are factors of ax2 + 5x + b show that a = b.
Answer:
P(x) = ax2 + 5x2 + b
x – 2 = 0
x = 2
P(x) = ax2 + 5x + b
P(2) = a(2)2 + 5(2) + b
0 = 4a + 10 + b ➝ (1)
P(x) = ax2 + 5x + b
x – \(\frac{1}{2}\) = 0
x = \(\frac{1}{2}\)
P(x) = ax2 + 5x + b

a = – 2 ➝ (3)
Put a = – 2 in equation (1)
4a – 10 + b = 0
4(- 2) + 10 + b = 0
– 8 + 10 + b = 0
2 + b = 0
b = -2 ➝ (4)
From (3) and (4)
a = b.
Question 11.
If α and β are the zeroes of the quadratic polynomials f(x) = 2x2 – 5x + 7, find a polynomial whose zeroes are 2α + 3β and 3α + 2β.
Answer:
Since α and β are the zeroes of the quadratic polynomial f(x) = 2x2 – 5x + 7.
Let S and P denote respectively the sum and product of the zeroes of the required polynomial.
Then, S = (2α + 3β) + (3α + 2β)
= 5(α + β) = 5 × \(\frac{5}{2}=\frac{25}{2}\) and
P = (2α + 3β) (3α + 2β)
⇒ P = (6α2 + 6β2 + 13αβ)
= 6α2 + 12αβ + αβ + 6β2
⇒ P = 6(α2 + β2 + 2αβ + αβ
= 6(α + β)2 + αβ
= 6(α2 + β2 + 2αβ) + αβ
= 6(α + β)2 + αβ
Hence the required polynomial g(x) is given by
g(x) = K(x2 – 5x + P)
or g(x) = K\(\left(x^{2}-\frac{25}{2} x+41\right)\), where K and any non zero real number.
Question 12.
If α and β are the zeroes of the polynomial. 6y2 – 7y + 2, find a quadratic polynomial whose zeroes are \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\).
Answer:
Let P(y) = 6y2 – 7y + 2

![]()
Question 13.
If one zero of the polynomial 3x2 – 8x + 2k + 1 and seven times the other, find the value of k.
Answer:
Let α and β be the zeroes of the polynomial. Then as per question β = 7α.
Now sum of zeroes = α + β = α + 7α
Question 14.
If one zero of polynomial (a2 + 9)x2 + 13x + 6a and reciprocal of the other, find the value of a.
Answer:
Let one zero of the given polynomial be α
Then, the other zero and \(\frac{1}{\alpha}\)
∴ Product of zeroes = α × \(\frac{1}{\alpha}\) = 1
But, as per the given polynomial product of Zeroes = \(\frac{6 a}{a^{2}+9}\)
∴ \(\frac{6 a}{a^{2}+9}\) = 1 ⇒ a2 + 9 = 6a
⇒a2 – 6a + 9 = 0 ⇒ (a – 3)2 = 0
⇒ a – 3 = 0 ⇒ a = 3
Hence a = 3.
Question 15.
Find the zeroes of the polynomial f(x) = x3 – 5x2 – 2x + 24 if it is given that the product of its two zeroes is 12.
Answer:
Let α, β and γ be the zeroes of polynomial f(x) such that αβ = 12
Putting αβ = 12 in αβγ = – 24 we get
12γ = – 24 ⇒ γ = \(\frac{-24}{12}\) = – 2
Now α + β + γ = 5 ⇒ α + β – 2 = 5
⇒ α + β = 7
⇒ α = 7 – β
∴ αβ =12
⇒ (7 – β) β = 12
⇒ 7β = β2 = 12
⇒ β2 – 7β + 12 = 0
⇒ β2 – 3β – 4β – 12 = 0
⇒β(β -3) – 4(β – 3) = 0
⇒(β -4)(β – 3) = 0
⇒ β = 4 or β = 3
α = 3 or α = 4.
Question 16.
If α, β, γ be zeroes of polynomial 6x3 + 3x2 – 5x +1, then find the value of α– 1 + β– 1 + γ– 1
Answer:
P(x) = 6x3 + 3x2 – 5x + 1 so
a = 6, b = 3, c = – 5, d = 1
∴ α, β and γ are zeroes of the polynomial p(x)

![]()