Students can Download Chapter 10 Mensuration Ex 10.3 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 6 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 6 Maths Chapter 10 Mensuration Ex 10.3
Question 1.
Find the areas of the rectangles whose sides are:
a) 3 cm and 4 cm
b) 12 m and 21 m
c) 2 km and 3 km
d) 2m and 70cm.
Solution:
It is known that
Area of rectangle = length × Breadth
a) 1 = 3 cm, b = 4 cm Area = l × b = 3 × 4 = 12 cm2
b) 1 = 12 m, b = 21 m
Area = l × b = 12 × 21 = 252 m2
c) l = 2 km, b = 3 km
Area = l × b = 2 × 3 = 6km2
d) l = 2 m , b = 70 cm = 0.70 m
Area = l × b = 2 × 0.70 = 1.40 m2
![]()
Question 2.
Find the areas of the squares whose sides are:-
a) 10 cm
b) 14 cm
c) 5 m
Solution:
It’s known that, Area o f square = side × side
a) 10cm
side = 10 cm
Area of the square =10 × 10= 100 cm2
b) 14 cm
side = 14 cm
Area of the square = 14 × 14 = 196 cm2
c) 5m
Side = 5 m
Area of the square = 5 × 5 = 25 m2
![]()
Question 3.
The length and breadth of three rectangles are as given below :
a) 9 m and 6 m
b) 17 m and 3 m
d) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solution:
It is known that
Area of rectangle = length × Breadth
a) l = 9 m b = 6 m
Area = l × b = 9 × 6 = 54 m2
b) l = 17 m b = 3 m
Area = l × b = 17 × 3 = 51 m2
c) l = 4 m b = 14 m
Area = l × b = 4 × 14 = 56 m2
It can be see that rectangle (c) has the largest area and rectangle (b) has the smallest area.
Question 4.
The areas of a rectangular garden 50m long is 300 sq m. Find the width of the garden.
Solution:
Given:-
Length of the garden = 50 m = l
and Areas of the garden = 300 sq m = A
Width or breadth = ? = b
A = l × b
300 = 50 × b

b = 6 m
The breadth or width of the garden = 6 m
Question 5.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of Rs 8 per hundred sq m.?
Solution:
Area of rectangular plot = 500 × 200 = 100000 m2
cost of tiling per 100 m2 = Rs. 8
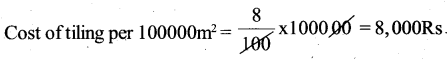
Question 6.
A table – top measures 2 m by 1 m 50 cm. What is its area in square metres?
Solution:
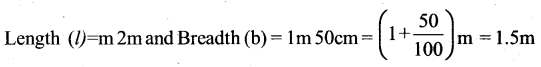
Areas = 1 × 6 = 2 × 1.5 = 3m2
![]()
Question 7.
A room is 4 m long and 3 m 50 cm wide . How many square metres of carpet is needed to cover the floor of the room?
Solution:
Length (l) = 4 m,
Breadth (b) = 3 m 50 cm = 3.5 m
Area = l × b = 4 × 3.5 = 14 m2
Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:
Length (l) = 5 m,
Breadth (b) = 4 m
Area = l × b = 5 × 4 = 20 m2
Area covered by the carpet = (side)2 = (3)2 = 9 m2
Area not covered by the carpet = 20 – 9 = 11 m2
Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5m long and 4m wide. What is the area of the remaining part of the land?
Solution:
Area of the land = 5 × 4 = 20 m2
Area occupied by 5 flower beds = 5 × (side)2 = 5 × (1 )2 = 5m2
Areas of the remaining part = 20 – 5 = 15 m2
![]()
Question 10.
By splitting the following figures into rectangles, find their areas ( The measures are given in centimetres).
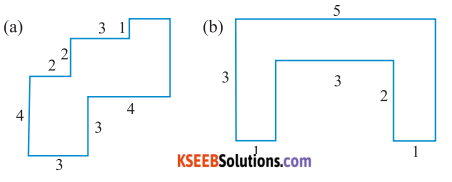
Solution :
(a) The given figure can be broken into rectangles as follows.
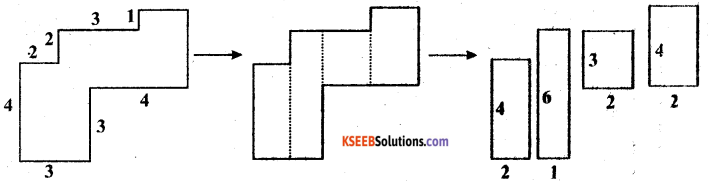
Area of 1st rectangle = 4 × 2 = 8 cm2
Area of 2nd rectangle = 6 × 1 = 6 cm2
Area of 3rd rectangle = 3 × 2 = 6 cm2
Area of 4th rectangle = 4 × 2 = 8 cm2
Total area of the complete figure = 8 + 6 + 6 + 8 = 28 cm2
(b) The given figure can be broken into rectangles as follows.
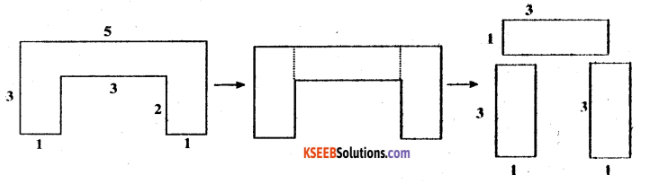
Area of 1st rectangle = 3 × 1 = 3 cm2
Area of 2nd rectangle = 3 × 1 = 3 cm2
Area of 3rd rectangle = 3 × 1 = 3 cm2
Total area of the complete figure = 3 + 3 + 3 = 9 cm2
Question 11.
Split the following shapes into rectangles and find their areas.( The measures are given in centimetres)
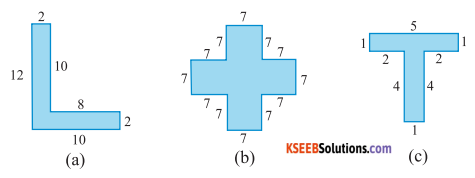
Solution:
(a) The given figure can be broken into rectangles as follows.
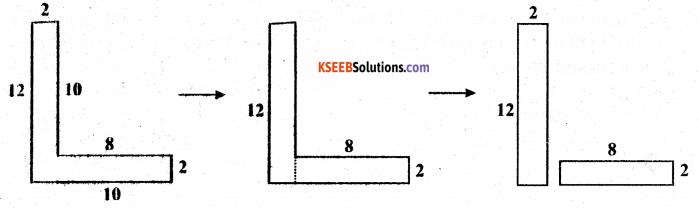
Area of 1st rectangle = 12 × 2 = 24 cm
Area of 2nd rectangle = 8 × 2 = 16 cm
Total area of the complete figure = 24 + 16 = 40 cm
(b) The given figure can be broken into rectangles as follows.
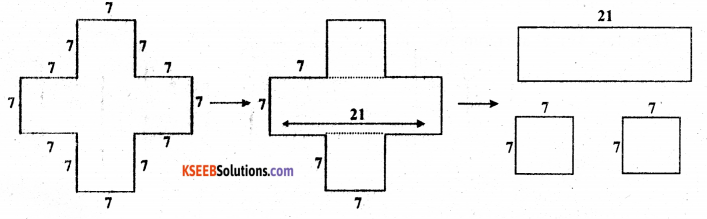
Area of 1st rectangle = 21 × 7 = 147 cm
Area of 2nd square = 7 × 7 = 49 cm
Area of 3rd square = 7 × 7 = 49 cm
Total area of the complete figure = 147 + 49 + 49 = 245 cm
![]()
(c) The given figure can be broken into rectangles as follows:
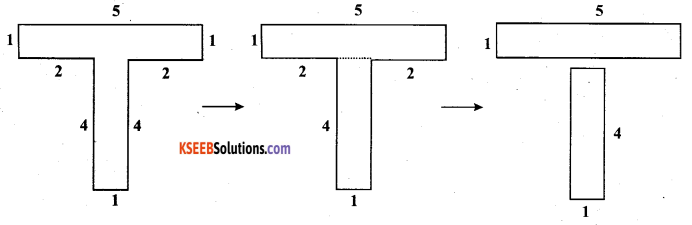
Area of 1st rectangle = 5 × 1 = 5 cm
Area of 2nd rectangle = 4 × 1 = 4 cm
Total area of the complete figure = 5 + 4 = 9 cm
![]()
Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
a) 100 cm and 144 cm
b) 70 cm and 36 cm.
Solution:
(a) Total area of the region = 100 × 144 = 14400 cm2
Area of one tile = 12 × 5 = 60 cm2
img class=”alignnone size-full wp-image-45590″ src=”https://ktbssolutions.com/wp-content/uploads/2020/10/KSEEB-Solutions-for-Class-6-Maths-Chapter-10-Mensuration-Ex-10.3-60.png” alt=”KSEEB Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3 60″ width=”433″ height=”57″ />
Therefore, 240 tiles are required.
(b) Total area of the region = 70 × 36 = 2520 cm2
Area of one tile = 60 cm2
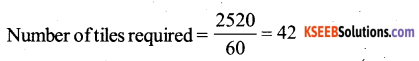
Therefore, 42 tiles are required.