Students can Download Chapter 11 Algebra Ex 11.5 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 6 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 6 Maths Chapter 11 Algebra Ex 11.5
Question 1.
State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
Solution:
a) 17 = x + 7
An equation with variable x
b) (t – 7) > 5
An inequality
c) \(\frac{4}{2}\) = 2
No, it is a numerical equation
d) (7 × 3) – 19 = 8
No, it is a numerical equation
e) 5 × 4 – 8 = 2x
An equation with variable x
![]()
f) x – 2 = 0
An equation with variable x
g) 2m < 30
An inequality
h) 2n + 1 = 11
An equation with variable n
i) 7 = (11 × 5) – (12 × 4)
No, it is a numerical equation
j) 7 = (11 × 2 ) + p
An equation with variable p
k) 20 = 5y
An equation with variable y
l) \(\frac{3 p}{2}\) < 5 An inequality m) z + 12 > 24
An inequality
n) 20 – (10 – 5) = 3 × 5
No, it is a numerical equation
o) 7 – x = 5
An equation with variable x.
![]()
Question 2.
Complete the entire in the third column of the table.
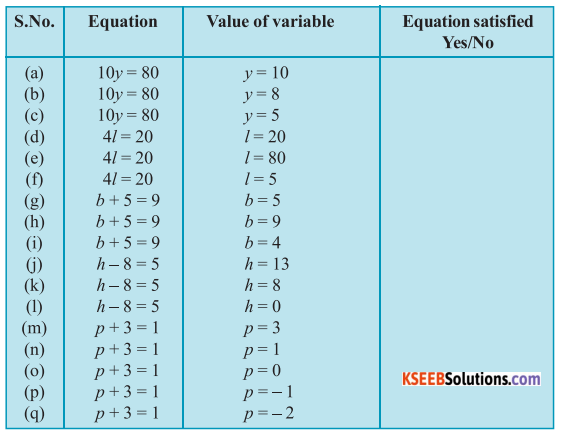
Solution:
a) 10y = 80
y = 10 is net a solution to the given equation because for y = 10
10y = 10 × 10 = 100, and net 80
b) 10y = 80
y = 8 is a solution to the given equation because for y = 8
10y = 10 × 8 = 80 and hence, the equation is satisfied
c) 10y = 80
y = 5 is net a solution to the given equation because for y = 5
10y = 10 × 5 = 50, and net 80.
d) 4l = 20
l = 20 is net a solution to the given equation because for l = 20
4l = 4 × 20 = 80, and net 20
e) 4l = 80
l = 80 is net a solution to the given equation because for l = 80
4l = 4 × 80 = 320, and net 20
f) 4l = 20
4l = 4 × 5 = 20 and hence, the equation because for l = 5
4l = 4 × 5 = 20 and hence, the equation is satisfied
g) b + 5 = 9
b = 5 is net a solution to the given equation because for b = 5
h) b + 5 = p
b = 9 is net a solution to the given equation because for b = 9
b + 5 = 9 + 5 = 14, and net 9
i) b + 5 = 9
b + 5 = 4 + 5 = 9 and hence, the equation is satisfied
![]()
j) h – 8 = 5
h = 13 is a solution to the given equation because for h = B
h – 8 = 13 – 8 = 5 and hence, the equation is satisfied
k) h – 8 = 5
h = 8 is net a solution to the given equation because for h = 8
h = 8 = -8 = 0, and net 5
l) h – 8 = 5
h = 0 is net a solution to the given equation because for h = 0,
h – 8 = 0 – 8 = -8, and net 5
m) p + 3 = 1
p + 3 = 3 + 3 = 6, and net 1
n) p + 3 = 1
p + 3 = 1 + 3 = 4 , and net 1
o) p + 3 = 1
p + 3 = 0 + 3 = 3, and net 1
p) p + 3 = 1
p + 3 = -1 + 3 = 2, and net 1
p + 3 = -2 + 3 = 1 and hence, the equation is satisfied.
![]()
Question 3.
Pick out the solution from the values given in the bracket next to each equation. show that the other values do not satisfy the equation.
Solution:
a) 5m = 60 (10, 5, 12, 15)
m = 12 a solution to the given equation because form = 12
5m = 5 × 12 = 60 and hence, the equation is satisfied
m = 10 is not a solution to the given equation because for m = 10.
5m = 5 × 10 = 50, and net 60
m = 5 is net a solution to the given equation because for m = 5,
5m = 5 × 5 = 25, and net 60
m = 15 is net a solution to the given equation because for m = 15
5m = 5 × 15 = 75, and net 6.
b) n + 12 = 20 (12, 8, 20, 0)
n = 8 is a solution to the given equation because for n = 8
n + 12 = 8 + 12 = 20 and hence, the equation is satisfied
n +12 = 12 + 12 = 24, and net 20
n = 20 is net a solution to the given equation because for n = 20
n + 12 = 20 + 12 = 32, and net 20
c) p – 5 = 5 (0, 10, 5 – 5)
p = 10 is a solution to the given equation because for p = 10, p – 5 = 10 – 5 = 5 and hence, the equation is satisfied.
p = 0 is net a solution to the given equation because for p = 0 .
p – 5 = 5 – 5 = 0, and net 5
p = -5 is net s solution to the given equation because for p = -5
p = 5 = -5 – 5 = -10 and net 5
d) \(\frac{q}{2}\) = 7 (7, 2, 10, 14)
q = 14 is a solution to the given equation because for q = 7 \(\frac{q}{2}\) = \(\frac{7}{2}\) and not 7
\(\frac{q}{2}\) = \(\frac{7}{2}\) and net 7
q = 2 is not a solution to the given equation because for q = 7
\(\frac{q}{2}\) = \(\frac{7}{2}\) and net 7
q = 2 is net a solution to the given equation because for q = 2
\(\frac{q}{2}\) = \(\frac{2}{2}\) = 1, and net 7
q = 10 is net a solution to the given equation because for qn = 10,
\(\frac{q}{2}\) = \(\frac{10}{2}\) = 5, and net 7
e) r – 4 = 0 (4, -4, 8, 0)
r = 4 is a solution to the given equation because for r = 4
r = 4 = 4 – 4 = 0 and hence, the equation is satisfied
r = -4 is net a solution to-the given equation because for r = -4
r – 4 = -4 – 4 = -8 and net 0
r = 8 is net a solution to the given equation because for r = 8
r – 4 = 8 – 4 = 4 and net 0
r = 0 is net a solution to the given equation because for r = 0
r – 4 = 0 – 4 = -4 and net 0 .
f) x + 4 = 2 (-2, 9, 2, 4)
x = -2 is a solution to the given equation because for x – 2
x + 4 = -2 + 4 = 2 and hence, the equation is satisfied
x = 0 is net a solution to the given equation because for x = 0
x + 4 = 0 + 4 = 4 and net 2
x = 2 is net a solution to the given equation because for x = 2
x + 4 = 2 + 4 = 6 and net 2
x = 4 is net a solution to the given equation because for x = 4
x + 4 = 4 + 4 = 8, and net 2.
![]()
Question 4.
a) Complete the table and by inspection of the table find the solution to the equation m +10 = 6

Solution:
By inspection, we can find that m = 6 is the solution of the above equation as for m = 6, m + 10 = 6 + 10 = 16
b) Complete the table and by inspection of the table, find the solution to the equation 5t = 35

Solution:
For 5t, the table can be constructed as follows
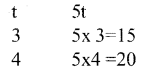

By inspection, we can find that t = 7 is the solution of the above equation as for t = 7, 5t = 5 × 7 = 35
c) Complete the table and find the solution of the equation x/3 = 4 using the table.
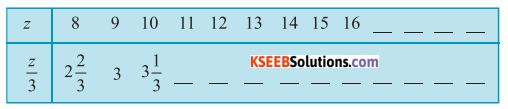
Solution:
For, the table can be constructed as follows
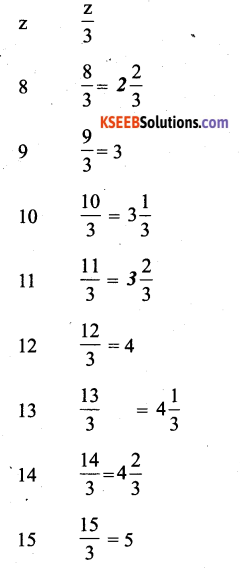
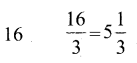
By inscription, we can find that z = 12 is the solution of the above equation of the above equation as for z = 12, \(\frac{z}{3}\) = 4
![]()
d) Complete the table and find the solution to the equation m – 7 = 3

Solution:

By inspection, we can find that m = 10 is the solution of the above equation as for m = 10, m – 7 = 10 – 7 = 3
![]()
Question 5.
Solve the following riddles, you may yourself construct such riddles. Who am I?

i) Go round a square
Counting every corner
Thrice and no more!
Add the count to me
To get exactly thirty four!
Solution:
There are 4 comers in a square
Thrice the number of comers in the square will be 3 × 4 = 12
When this result result i,e 12, is added to the number if Comes to be 34. therefore the number will be the difference of 34 and 12 i.e 34 – 12 = 22
ii) For each day of the week
Make an upcount from me
If you make mo mistake
you will get twenty three!
Solution:
23 was the result when the old number was up Counted on Saturday
22 was the result when the old number was up counted on Saturday
20 was the result ‘when the old number was up counted on Thursday
19 was the result when the old number was up counted on tuesday
18 was the result when the old number was up counted on Tuesday
17 was the result when the old number was up counted on Tuesday
iii) I am a special number
Take away from me a six!
A whole cricket term
you will still be able to fix!
Solution:
In a cricket taken at the 11 players Hence the number is such that when 6 is subtracted from it, the result is 11, Therefore, the number is 11 + 6 = 17
iv) Tell me who I am
I shall give a pretty clue!
you will get me back
If you take me out of twenty two!
Solution:
The number is such that when it is subtracted from 22 the result is again the number it self the number is 11, when again gives 11, when it is subtracted from 22.