Students can Download Chapter 14 Practical Geometry Ex 14.4 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 6 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 6 Maths Chapter 14 Practical Geometry Ex 14.4
Question 1.
Draw any line segment \(\overline{\mathbf{A B}}\). Mark any point M on it. Through M, draw a perpendicular to \(\overline{\mathbf{A B}}\). (use ruler and compasses)
Solution:
(1) Draw the given line segment \(\overline{\mathbf{A B}}\) and mark an point M on it.
(2) With M as centre and a convenient radius, construct an arc intersecting the line segment \(\overline{\mathbf{A B}}\) at two points C and D.
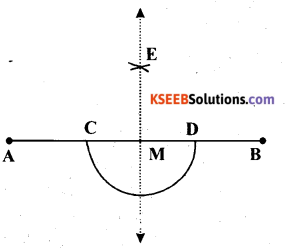
(3) With C and D as centres and a radius greater than CM, construct two arcs. Let these be intersecting each other at E.
(4) Join EM. \(\overline{\mathrm{EM}}\) is perpendicular to AB
![]()
Question 2.
Draw a line segment \(\overline{\mathrm{AB}}\) Take any point R not on it. Through R, draw a perpendicular to \(\overline{\mathrm{AB}}\). (use ruler and set-square)
Solution:
(1) Take the given line segment \(\overline{\mathrm{PQ}}\) and mark any point R outside \(\overline{\mathrm{PQ}}\).
(2) Place a set square on \(\overline{\mathrm{PQ}}\) such that one arm of its right angle aligns along \(\overline{\mathrm{PQ}}\).
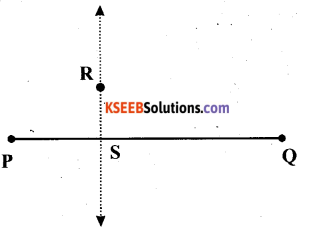
(3) Place the ruler along the edge opposite to the right P angle of the set square.
(4) Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.
(5) Draw a line along this edge of the set square which will be passing through R. It is the required line, which is perpendicular to \(\overline{\mathrm{PQ}}\).
![]()
Question 3.
Draw a line l and a point X on it. Through X, draw a line segment \(\overline{\mathrm{XY}}\) perpendicular to l.
Now draw a perpendicular to \(\overline{\mathrm{XY}}\) at Y. (use ruler and compasses)
Solution :
(1) Draw a line l and mark a point X on it.
(2) Taking X as centre and with a convenient radius, draw an arc intersecting line 1 at two points A and B.
(3) With A and B as centres and a radius more than AX, construct two arcs intersecting each other at Y.
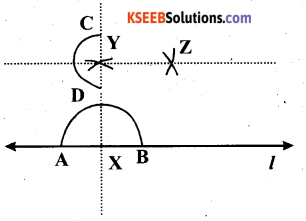
(4) Join XY. \(\overline{\mathrm{XY}}\) is perpendicular to l.
Similarly, a perpendicular to \(\overline{\mathrm{XY}}\) at point Y can be drawn. The line \(\overline{\mathrm{ZY}}\) is perpendicular t0 \(\overline{\mathrm{XY}}\) at Y.