KSEEB Solutions for Class 8 Maths Chapter 11 Mensuration InText Questions

You can Download KSEEB Solutions for Class 8 Maths Chapter 11 Mensuration InText Questions and Answers helps you to revise the complete syllabus.

KSEEB Solutions for Class 8 Maths Chapter 11 Mensuration InText Questions

Try These (Page 170)

Question (a).
Match the following figures with their respective areas in the box.

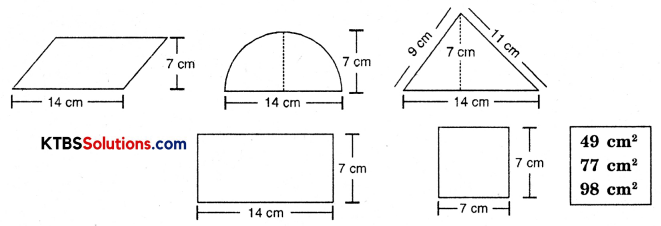
Solution:

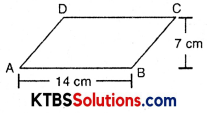
Area of parallelogram ABCD
= Base × height
= 14 × 7
= 98 cm²

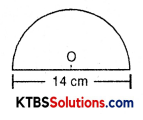
Area of semicircle = \(\frac{1}{2} \pi r^{2}\)
= \(\frac{1}{2} \times \frac{22}{7} \times \frac{14}{2} \times \frac{14}{2}\)
= 77 cm²

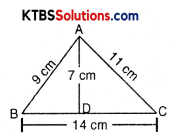
Area of triangle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 14 × 7
= 49 cm²

Area of rectangle = l × b
= 14 × 7
= 98 cm²

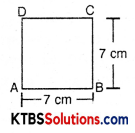
Area of square = (side)²
= 7 × 7
= 49 cm²

Question (b).
Write the perimeter of each shape.
Solution:
Perimeter of parallelogram = 2(14 + b) cm

Perimeter of semicircle = \(\frac{2 \pi r}{2}\)
= πr
= \(\frac{22}{7}\) × 7
= 22 cm

Perimeter of triangle = (14 + 11 + 9)
= (14 + 20)
= 34 cm

Perimeter of rectangle = 2(l + b)
= 2 (14 + 7)
= 2(21)
= 42 cm

Perimeter of square = 4 × side
= 4 × 7
= 28 cm

Try These (Page 172)

Question 1.
Nazma’s sister also has a trapezium-shaped plot. Divide it into three parts as shown in the figure below. Show that the area of trapezium WXYZ = \(h \frac{(a+b)}{2}\)

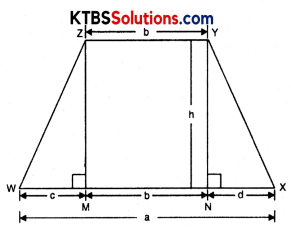
Solution:
Draw ZM ⊥ XW and YN ⊥ XW
Now, trapezium XYZW is divided into three parts. Two triangles and one rectangle.

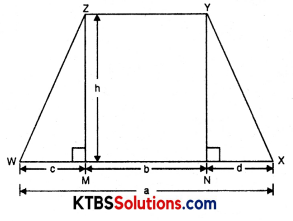
area of ΔZWM = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × c × h
area of ΔYNX = \(\frac{1}{2}\) × d × h
area of rectangle NYZM = b × h
area of trapezium XYZW = area of ΔZWM + area of ΔYNX + area of rectangle NYZM
= \(\frac{1}{2}\) × c × h + \(\frac{1}{2}\) × d × h + b × h
= \(h\left[\frac{1}{2} c+\frac{1}{2} d+b\right]\)
= \(h\left[\frac{c+d+2 b}{2}\right]\)
= \(h\left[\frac{c+d+b+b}{2}\right]\)
= \(h \frac{(a+b)}{2}\)

Question 2.
If h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, find the values of each of its parts separately and add to find the area WXYZ. Verify it by putting the values of h, a and b in the expression \(\frac{h(a+b)}{2}\)
Solution:
h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm

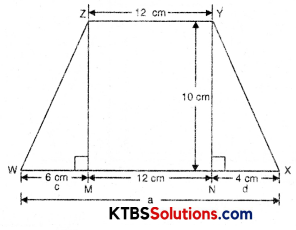
area of ∆ZWM = \(\frac{1}{2}\) × c × h
= \(\frac{1}{2}\) × 6 × 10
= 30 cm²
area of ∆YNX = \(\frac{1}{2}\) × d × h
= \(\frac{1}{2}\) × 4 × 10
= 20 cm²
area of rectangle = b × h
= 12 × 10
= 120 cm²
Area of trapezium XYZW = 30 + 20 + 120 = 170 cm²
area of trapezium XYZW = \(\frac{h(a+b)}{2}\)
= \(\frac{h[c+d+b+b]}{2}\)
= \(\frac{10[6+4+12+12]}{2}\)
= 5(34)
= 170 cm²

Try These (Page 173)

Question 1.
Find the area of the following trapeziums.

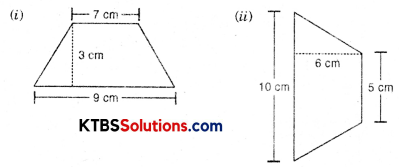
Solution:
(i) Area of trapezium = \(\frac{1}{2}\) (Sum of parallel side) × h
= \(\frac{1}{2}\) (9 + 7) × 3
= \(\frac{1}{2}\) × 16 × 3
= 24 cm²

(iii) Area of trapezium = \(\frac{1}{2}\) (Sum of parallel side) × h
= \(\frac{1}{2}\) (10 + 5) × 6
= \(\frac{1}{2}\) × 15 × 6
= 15 × 3
= 45 cm²

Try These (Page 174)

Question 1.
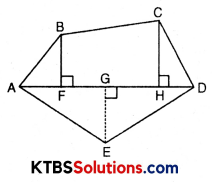
We know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral into two triangles, find their areas, and hence, that of the parallelogram. Does this agree with the formula that you know already? (Fig. 11.12).

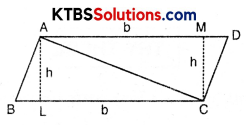
Solution:
Area of parallelogram = Base × Altitute
Area of parallelogram = Area of two triangles
= \(\frac{1}{2}\) × base × height + \(\frac{1}{2}\) × base × height
= 2 × \(\frac{1}{2}\) × b × h
= b × h
∴ b × h = b × h
Yes, this agrees with the formula that we already know. It means an area of a parallelogram is also equal to the sum of the area of two triangles.

Try These (Page 175)

Question 1.
Find the area of these quadrilaterals.

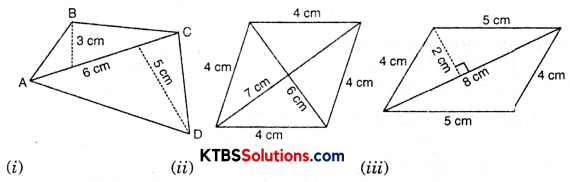
Solution:

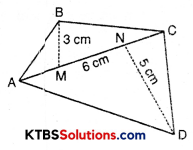
(i) Area of quadrilateral ABCD = ar ΔABC + ar ΔACD
= \(\frac{1}{2}\) × AC × BM + \(\frac{1}{2}\) × AC × CN
= \(\frac{1}{2}\) × 6 × 3 + \(\frac{1}{2}\) × 6 × 5
= 3 × 3 + 3 × 5
= 9 + 15
= 24 cm²

(ii) Area of trapezium = \(\frac{1}{2}\) × d₁ × d₂
= \(\frac{1}{2}\) × 7 × 6
= 21 cm²

(iii) Area of parallelogram = 2 area of Δ
= 2 × \(\frac{1}{2}\) × b × h
= 2 × \(\frac{1}{2}\) × 8 × 2
= 16 cm²

Try These (Page 176)

Question (i).
Divide the following polygons into parts (triangles and trapezium) to find out their area.

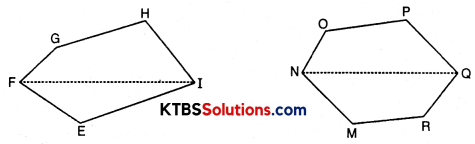
FI is a diagonal of polygon EFGHI; NQ is a diagonal of polygon MNOPQR
Solution:
Polygon EFGHI is divided into two parts. ΔEFG and trapezium EIHG.
Polygon MNOPQ is divided into two triangles OPN and MRQ and trapezium PQMN.

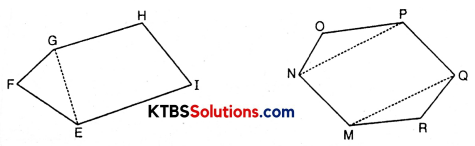
Question (ii).
Polygon ABCDE is divided into parts as shown below. Find its area if AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and perpendiculars BF = 2 cm, CH = 3 cm, EG = 2.5 cm.

Area of Polygon ABCDE = area of ΔAFB + ……..
Area of ΔAFB = \(\frac{1}{2}\) × AF × BF = \(\frac{1}{2}\) × 3 × 2 = …….
Area of trapezium FBCH = FH × \(\frac{(B F+C H)}{2}\) = 3 × \(\frac{(2+3)}{2}\) [FH = AH – AF]
Area of ΔCHD = \(\frac{1}{2}\) × HD × CH = …….., Area of ΔADE = \(\frac{1}{2}\) × AD × GE = …. So, the area of polygon ABCDE = …….
Solution:
Area of polygon ABCDE = area of ΔAFB + area of trapezium FBCH + area of ΔCHD + area of ΔADE
= \(\frac{1}{2}\) × AF × BF + \(\frac{F H \times(B F+C H)}{2}\) + \(\frac{1}{2}\) × HD × CH + \(\frac{1}{2}\) × AD × GE
= \(\frac{1}{2}\) × 3 × 2 + \(\frac{(A H-A F) \times[2+3]}{2}\) + \(\frac{1}{2}\) × (AD – AH) × 3 + \(\frac{1}{2}\) × 8 × 2.5
= 3 + \(\frac{(6-3)(5)}{2}+\frac{1}{2}\) × (8 – 6) × 3 + 10
= 3 + \(\frac{15}{2}+\frac{1}{2}\) × 2 × 3 + 10
= 13 + \(\frac{15}{2}+\frac{6}{2}\)
= \(\frac{26+15+6}{2}\)
= \(\frac{47}{2}\)
= 23.5 cm²

Question (iii).
Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm.
NA, OC, QD and RB are perpendiculars to diagonal MP.

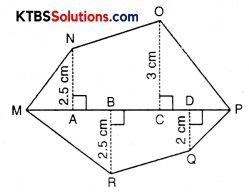
Solution:
Area of polygon MNOPQR = area of ∆AMN + area of trapezium ANOC + area of ∆OCP + area of ∆PDQ + area of trap. BDQR + area of ∆MBR
= \(\frac{1}{2}\) × AM × AN + \(\frac{1}{2}\) (AN + OC) × AC + \(\frac{1}{2}\) × CP × OC + \(\frac{1}{2}\) × DP × DQ + \(\frac{1}{2}\) (BR + DQ) × BD + \(\frac{1}{2}\) × MB × BR
= \(\frac{1}{2}\) × 2 × 2.5 + \(\frac{1}{2}\) (2.5 + 3) × (MC – AM) + \(\frac{1}{2}\) × (MP – MC) × 3 + \(\frac{1}{2}\) × (MP – MD) × 2 + \(\frac{1}{2}\) (2.5 + 2) × (MD – MB) + \(\frac{1}{2}\) × 4 × 2.5
= 2.5 + \(\frac{1}{2}\) × 5.5(6 – 2) + \(\frac{1}{2}\) (9 – 6) × 3 + \(\frac{1}{2}\) (9 – 7) × 2 + \(\frac{1}{2}\) × 4.5(7 – 4) + 5
= 2.5 + \(\frac{1}{2}\) × 5.5 × 4 + \(\frac{1}{2}\) × 3 × 3 + \(\frac{1}{2}\) × 2 × 2 + \(\frac{1}{2}\) × 4.5 × 3 + 5
= 2.5 + 11 + \(\frac{9}{2}\) + 2 + \(\frac{13.5}{2}\) + 5
= 15.5 + \(\frac{9}{2}+\frac{13.5}{2}\) + 5
= \(\frac{31+9+13.5+10}{2}\)
= \(\frac{63.5}{2}\)
= 31.75 cm²

Try These (Page 181)

Question 1.
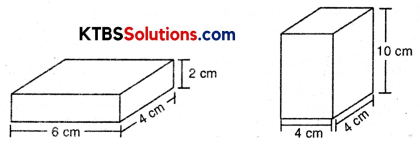
Find the total surface area of the following cuboids:

Solution:
(i) Length (l) of cuboid = 6 cm
Breadth (b) of cuboid = 4 cm
Height (h) of cuboid = 2 cm
Total surface area of cuboid = 2(lb + bh + lh)
= 2(6 × 4 + 4 × 2 + 2 × 6]
= 2[24 + 8 + 12]
= 2 × 44
= 88 cm²

(ii) Length (l) of cuboid = 4 cm
Breadth (b) of cuboid = 4 cm
Height (h) of cuboid = 10 cm
Total surface area of cuboid = 2 (lb + bh + lh)
= 2(4 × 4 + 4 × 10 + 10 × 4)
= 2[16 + 40 + 40]
= 2 × 96
= 192 cm²

Try These (Page 182)

Question 1.
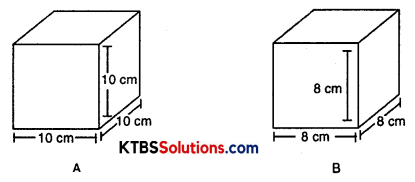
Find the surface area of cube A and lateral surface area of cube B.

Solution:
(A) Side of cube = 10 cm
Surface area of cube = 6(side)²
= 6(10)²
= 6 × 100
= 600 cm²

(B) Side of cube B = 8 cm
Lateral surface area of cube B = 4(side)²
= 4(8)²
= 4 × 64
= 256 cm²

Try These (Page 184)

Question 1.
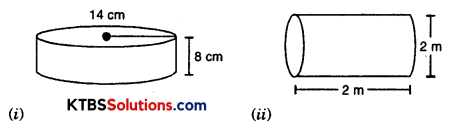
Find the total surface area of the following cylinders.

Solution:
(i) Radius of cylinder = 14 cm
Height of cylinder = 8 cm
Total surface area of cylinder = CSA of cylinder + area of bar
= 2πrh + 2πr²
= 2πr(h + r)
= 2 × \(\frac {22}{7}\) × 14[8 + 14]
= 2 × 22 × 2[8 + 14]
= 88 × 22
= 1936 cm²

(ii) Height of cylinder = 2 m
Diameter of cylinder = 2 m
Total surface area of cylinder = 2πrh + 2πr²
= 2πr(h + r)
= 2 × \(\frac {22}{7}\) × 1(2 + 1)
= \(\frac{44}{7}\) × 3
= \(\frac{132}{7}\)
= 18.86 cm² (approx.)

Try These (Page 188)

Question 1.
Find the volume of the following cuboids.

Solution:
(i) Length of cuboid (l) = 8 cm
Breadth of cuboid (b) = 3 cm
Height of cuboid (h) = 2 cm
Volume of cuboid = l × b × h
= 8 × 3 × 2
= 48 cm³

(ii) Area of base = 24 m²
Height of cuboid = 3 cm = \(\frac{3}{100}\) m
Volume of cuboid = Area of base × height
= 24 × \(\frac{3}{100}\)
= \(\frac{72}{100}\)
= 0.72 m³

Try These (Page 189)

Question 1.
Find the volume of the following cubes:
(a) with a side 4 cm
(b) with a side 1.5 m
Solution:
(a) Side of cube = 4 cm
Volume of cube = (Side)³
= (4)³
= 64 cm³

(b) Side of cube = 1.5 m
Volume of cube = (Side)³
= (1.5)³
= 1.5 × 1.5 × 1.5
= 3.3750 m³

Try These (Page 189)

Question 1.
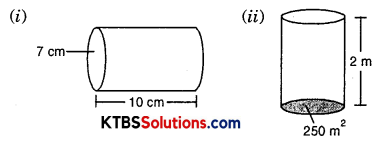
Find the volume of the following cylinders.

Solution:
(a) Radius of cylinder = 7 cm
Height of cylinder = 10 cm
Volume of cylinder = πr²h
= \(\frac{22}{7} \times(7)^{2} \times 10\)
= \(\frac{22}{7}\) × 7 × 7 × 10
= 154 × 10
= 1540 cm³

(b) Area of base = 250 m²
Height of cylinder = 2 m
Volume of cylinder = Area of base × height
= 250 × 2
= 500 m³