Students can Download Maths Chapter 13 Statistics Additional Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 8 Maths Chapter 13 Statistics Additional Questions
Question 1.
Four alternative options are given for each of the following statements. Select the correct option.
(a) The size or width of the class – interval (0 – 4) is
A. 4
B. 5
C. 3
D. 0
Solution:
B. 5
![]()
(b) The midpoint of the class interval (10 – 19) is
A. 10
B. 14
C. 15
D. 14.5
Solution:
D. 14.5
(c) The difference between the highest and lowest scores of a distribution gives
A. class interval
B. class width
C. range
D. class limit
Solution:
C. range
(d) The number of times a particular observation (score) occurs in a data is called.
A. frequency
B. range
C. class interval
D. class limit
Solution:
A. frequency
(e) In inclusive form, the actual upper limit and lower limit of class interval (0 – 4) are
A. – 0.5 & 3.5
B. 0.5 & 4.5
C. -1 & 5
D. 1 & 5
Solution:
A. -0.5 & 3.5
(f) The height of a rectangle in a histogram represents
A. class interval
B. midpoint
C. frequency density
D. frequency
Solution:
D. frequency
(g) In a histogram, the width of the rectangle indicates
A. class interval
B. midpoint
C. frequency density
D. frequency
Solution:
A. class interval
(h) The mean of scores 10, 15, 12, 15, 15, is
A. 15
B. 13
C. 13.4
D. 14.3
Solution:
C. 13.4
![]()
(i) Class interval grouping of data is done when
A. The range of data is small
B. The range of data is large
C. The class intervals are small
D. Class intervals are large
Solution:
B. The range of data is large
(j) The mean of 6, 4, 7, x and 10 is 8. The value of x is
A. 10
B. 12
C. 14
D. 13
Solution:
D. 13
(k) If n = 10 and mean = 12 then Sfx is
A. 120
B. 1200
C. 12
D. 13
Solution:
A. 120
(l) The mean of first three multiples of 5 is
A. 5
B. 10
C. 15
D. 30
Solution:
B. 10
(m) The median of 37, 83, 70, 29, 32, 42, 40 is
A. 29
B. 30
C. 40
D. 42
Solution:
C. 40
(n) In ah inclusive class interval (10 – 14), the lower real, limit is
A. 9.5
B. 10.5
C. 13.5
D. 14.5
Solution:
A. 9.5
![]()
(o) In an exclusive class interval (10 – 20) the lower real limit is
A. 20
B. 10
C. 10.5
D. 20.5
Solution:
B. 10
(p) The mode of 2, 3, 3, 5, 3, 5, 7, 3, 5 is
A. 3
B. 5
C. 3 and 5
D. 3, 5, 7
Solution:
A. 3
(q) Forgiven two values of x, 16, 18 the frequencies are respectively 12 and 20. Then the mode is
A. 16
B. 18
C. 12
D. 20
Solution:
D. 20
(r) A collection of data having more than 3 modes is said to be
A. Unimode
B. bi-mode
C. trimode
D. multimode
Solution:
D. multimode
![]()
Question 2.
Prepare a frequency distribution table for the scores given.
42, 22, 55, 18, 50, 10, 33, 29, 17,
29, 29, 27, 34, 15, 40, 42, 40, 41,
35, 27, 44, 31, 38, 19, 54, 55, 38,
19, 20, 30, 42, 59, 15, 19; 27, 23,
40, 32, 28, 51
Take the class intervals as 10 – 20, 20 – 30, 30 – 40, 40 – 50, 50 – 60. From the frequency distribution table answer the following questions.
(i) What does the frequency, corresponding to the class interval 20 – 30 indicate?
(ii) In which class intervals are the scores 10, 20 and 30 included?
(iii) Find the range of the scores.
Solution:
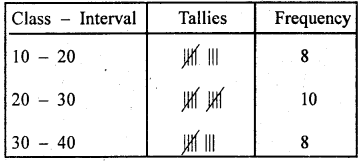
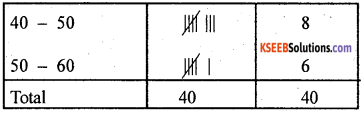
(i) The largest number of scores lie in the class interval 20 – 30
(ii) 10 is included in 10 – 20, 20 is included in 20 – 30 and 30 is in – eluded in 30 – 40.
(iii) The range = 59 – 10 = 49
Question 3.
The following are the marks scored in a unit test (out of 25). Prepare a frequency distribution table, taking the class intervals as 0 – 4, 5 – 9, 10 – 14, 15 – 19, 20 – 24.
21, 14, 3, 7, 23, 18, 24, 16, 18, 17, 20, 10, 17, 18, 21, 23, 19, 12, 14, 9, 16, 18, 12, 14, 11. From the table (i) find the midpoints of each class interval (ii) find the class interval having maximum frequency (iii) find the range of the scores.
Solution:
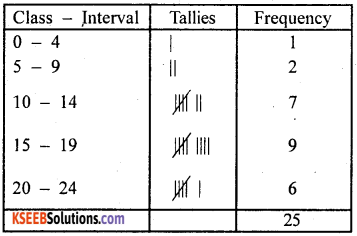
(i) Mid points of 0 – 4, 5 – 9, 10 – 14, 15 – 19 and 20 – 24 are 2, 7, 12, 17 and 22 respectively.
(ii) The class interval 15 – 19 has maximum frequency
(iii) Range = 24 – 3 = 21
![]()
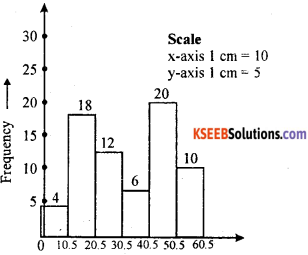
Question 4.
Draw a histogram for the following frequency distribution.

Solution:
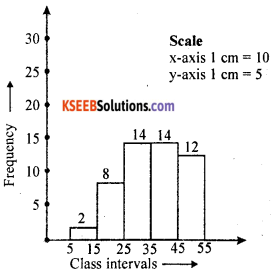
Question 5.
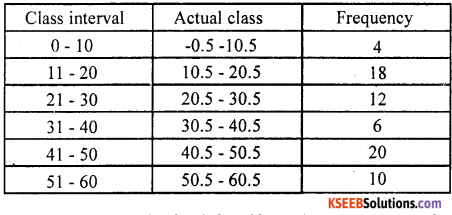
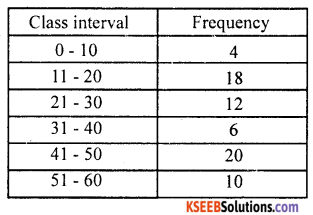
Draw a histogram for the following frequency distribution.
Solution:
The given distribution is in the inclusive form.
d = lower limit of a class – upper limit of a class before it = 11 – 10
d = 1, \(\frac{d}{2}\) = \(\frac{1}{2}\) = 0.5
Question 6.
The marks obtained by 12 students in a mathematics examination are given below 48, 78, 93, 90, 66, 54, 83, 58, 60, 75, 89, 84. Find (i) the mean of the marks (ii) the mean mark of the student if each student is given 4 grace marks.
Solution:
(i) ∑x = 48 + 78 + 93 + 90 + 66 + 54 + 83 + 58 + 60 + 75 + 89 + 84 = 878
N = 12
![]()
(ii) If each student is given 4 grace marks then the mean = 73.17 + 4 = 77.17
![]()
Question 7.
If the mean of 8, 12, 21, 42, x is 20 find the value of x.
Solution:
∑x = 8 + 12 + 21 + 42 + x = S3 + x N = 5 Mean – 20
Mean = \(\frac{\Sigma x}{N}\)
100 = 83 + x
100 – 83 = x
∴ x = 17
Question 8.
Find the mean for the following distribution 12, 14, 10, 12, 15, 12, 18, 10, 15, 11, 19, 20, 12, 15, 19, 10, 18, 16, 20, 17.
Solution:
∑x – 12 + 14 + 10 +12 +15 + 12 + 18 + 10 + 15 + 11 + 19 + 20 + 12 + 15 + 19 + 10 + 18 + 16 + 20 + 17 = 295
N = 20
![]()
![]()