Students can Download Maths Chapter 14 Introduction of Graphs Additional Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 8 Maths Chapter 14 Introduction of Graphs Additional Questions
Question 1.
Choose the correct option.
(a) The point (4, 0) lie on the line _______
A. y – x = 0
B. y = 0
C. x = 0
D. y + x = 0
Solution:
B. y = 0
![]()
(b) The point (-5, 4) lie in ___________
A. the first qudrant
B. the second quadrant
C. the third quadrant
D. the fourth quadrant
Solution:
B. the second quadrant.
(c) If a straight pass through (0, 0) and (1, 5) then its equation is ________
A. y = x
B. y = 5x
C. 5y = x
D. y = x + 5
Solution:
C. 5y = x
(d) If a point P has coordinates (3, 4) in coordinate system X’OX ↔ Y’OY and if O has coordinates (4, 3) in another system X’1OX1 ↔ Y1‘01Y1 is __________
A. (3, 4)
B. (1, -1)
C. (7, 7)
D. (-1, 1)
Solution:
C. (7, 7)
(e) The coordinates of a point P in a system X’OX ↔ Y’OY are (5, 8). The coordinates of the same point in the system Y’OY ↔ XOX’ are
A. (-8, 5)
B. (8, 5)
C. (8, -5)
D. (-8, -5)
Solution:
C. (8, -5)
![]()
(f) The signs of the coordinates of a point in the third quadrant are
A. (+, -)
B. (-, +)
C. (+, +)
D. (-, -)
Solution:
D. (-, -)
(g) If a person moves either 1 unit in the direction of the positive x-axis or 1 unit in the direction of positive y-axis per step; then the number of steps he requires to reach (10, 12) starting from the origin (0, 0) in
A. 10
B. 12
C. 22
D. 120
Solution:
C. 22
(h) They coordinate of the point of 2. intersection of the line y = 3x + 4 with
x = 3 is
A. 4
B. 7
C. 10
D. 13
Solution:
B. 7
(i) The equation of the line which passes through (0, 0) and (1, 1) is
A. y = x
B. y = – x
C. y = 1
D. x = 1
Solution:
A . v = x
Question 2.
Find the quadrant in which the following points lie.
Solution:
(i) (5, 10) – I Quadrant
(ii) (-8, 9) – II Quadrant
(iii) (-800, -3000) – III Quadrant
(iv) (8, -100) – IV Quadrant
![]()
Question 3.
Match the following
(A) on the x axis – (i) x coordinate is negative
(B) In th second quadrant – (ii) cuts the y axis at (0, 4)
(C) The line y = 3x + 4 – (iii) coordinates of a point are of form (a, 0)
Solution:
(A) – (iii)
(B) – (i)
(C) – (ii)
Question 4.
Fill in the blanks
(a) They coordinate of a point on the x-axis in zero.
(b) The x coordinate is called abscissa.
(c) The x-axis and y-axis intersect at (0, 0)
(d) If a point (x, y) ≠ (0, 0) is in the third quadrant, then (x + y) has a negative sign.
(e) If a point (x, y) lies above the horizontal axis, then y is always positive.
(f) The point of intersection of x = y and x = – y is (0, 0)
(g) The line y = 4x + 5 intersects y-axis at the point (0, 5)
![]()
Question 5.
True or false
(a) The equation of the x-axis is x = 0.
Answer:
False
(b) The line x = 4 is parallel to the y-axis.
Answer:
True
(c) The line y 8 is perpendicular to the x-axis.
Answer:
False
(d) The line x = y and x = – y are perpendicular to each other.
Answer:
True
(e) The lines x = 9 and y = 9 are perpendicular to each other.
Answer:
True
(f) The graph of y = x2 is a straight line.
Answer:
False
(g) The line y = 3x + 4 does not in¬tersect x-axis.
Answer:
False
(h) In a rectangular coordinate system, the coordinate axes are chosen such that they form a pair of perpendicular lines.
Answer:
True
![]()
Question 6.
Determine the equation of the line which passes through the points (0, -8) and (7, 0).
Solution:
Let the equation be y = ax + b. The line passes through (0, -8). When
x = 0 y = – 8
y = ax + b
– 8 = a (0) + b
– 8 = 0 + b
∴ b = – 8
The lines passes through (7, 0). When x = 7, y = 0
y = ax + b
0 = a (7) + b, 0 = 7a + b
0 = 7a – 8 (∴ b = – 8)
8 = 7a
a = \(\frac{8}{7}\)
y = ax + b
y = \(\frac{8}{7}\) x + (-8)
7y = 8x – 56
56 = 8x – 7y
∴ The equation is 8x – 7y = 56
![]()
Question 7.
Determine the equation of the line in each of the following graph.
(i)
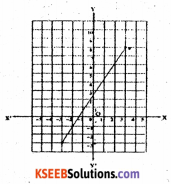
Solution:
From the graph we find that the line passes through the points (3, 8) and (-3, -3).
Let the equation be y = ax + b
When x = 3, y = 8
∴ 8 = a (3) + b
8 = 3a + b
∴ b = 8 – 3a
When x = – 3, y = – 3
∴ y = ax + b
– 3 = a(-3) + b
– 3 = – 3a + b
– 3 = – 3a + 8 – 3a [∴ b = 8 – 3a]
6a = 8 + 3
a = \(\frac{11}{6}\)
b = 8 – 3a
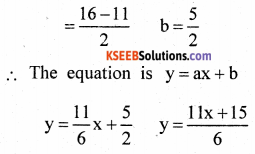
6y = 11x + 15
(ii)
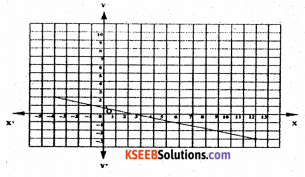
From the graph we find that the line passes through the points (-4, 2) and (12, -3)
Let the equation is y = ax + b
When x = – 4, y = 2
∴2 = a(-4) + b 2 = – 4a + b
b =2+ 4a
When x = 12, y = – 3, y = ax + b
– 3 = a(12) + b – 3 = 12a + b
– 3 = 12a + 2 + 4a [∴ b = 2 + 4a]
– 3 = 16a + 2 – 3 – 2 =16a
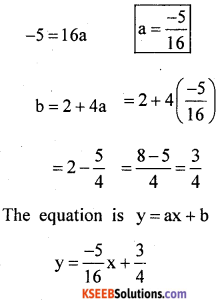
y = \(\frac{-5 x+12}{16}\)
16y = – 5x + 12
16y + 5x + = 12
![]()
Question 8.
A point P has coordinates (7, 10) in a coordinate system X’OX ↔ Y’OY. Suppose it has coordinates (10, 7) in another coordinate system X’1O1X1 ↔ Y’1O1y1 with X’OX || X’1O1X1.
Find the coordinates of O1 in the system X’OX ↔ Y’OY.
Solution:
Given P (x, y) = (7, 10) and (x’, y’) = (10, 7)
Let the coordinates of O1 in X’OX – Y”OY be (a, b)
x = a + x’ y = b + y’.
7 = a + 10
10 – b + 7
7 – 10 = a
10 – 7 = b
– 3 = a 3 = b
a = – 3 b = 3
∴The coordinates of O1 are (-3, 3)
Question 9.
Sketch the region {(x, y) : x > 0, y > 0, x + 2y < 4} in a coordinate system set up by you. Solution: Given x > 0, y > 0 x + 2y < 4
Let x = 0 and y = 1, .
then x + 2y = 0 + 2(1) = 0 + 2 = 2 < 4
x = 1 and y = 1,
then x + 2y + 1 + 2(1) = 1 + 2 = 3 < 4
x = 2 and y = 0, then x + 2y = 2 + 2(0) = 2 + 0 = 2 <4
x = 2 and y = 1
then x + 2y = 2 + 2(1) = 2 + 2 = 4
x = 0 and y = 0 then x + 2y = 0 + 2(0) = 0 + 0 = 0
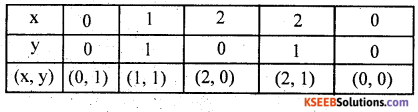
![]()
Question 10.
Draw the graphs of lines 3x = 4x – 4 and 2x = 3y + 4 and determine the point at which these lines meet.
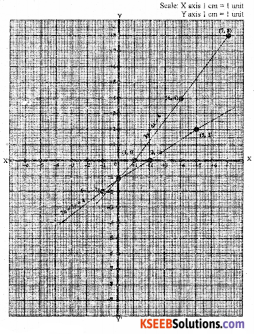
Solution:
3y = 4x – 4
2x = 3y + 4
y = \(\frac{4 x-4}{3}\)
2x – 4 = 3y
y = \(\frac{2 x-4}{3}\)
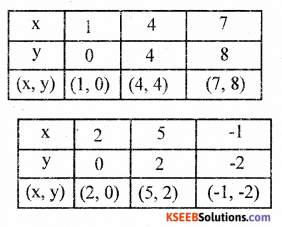
Question 11.
If a * b = ab + a + b, draw the graph of y = 3 * (x +1) * 2
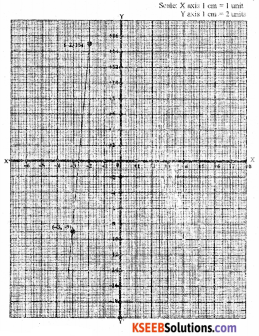
Solution:
3 * (x +1) * 2
Find 3 * (x + 1) Given a * b = ab + a + b
∴ 3 * (x + 1) = 3( x + 1) + 3 + (x + 1)
= 3x +1 + 3 + x +1
3 * (x +1) = 4x + 5
Now find 3 * (x +1) * 2
= (4x + 5) * 2 = (4x + 5)2 + 4x + 5 + 2
= 8x + 10 + 4x + 7
3 * (x + 1) * 2 = 12 x + 27
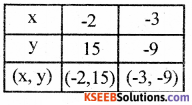
∴ y = 12x + 27
When x = – 2, = 12 (-2) + 27
= – 12 + 27 – 15
When x = – 3 y = 12 (-3) + 27
= – 36 + 27 = – 9
![]()