You can Download KSEEB Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 Questions and Answers helps you to revise the complete syllabus.
KSEEB Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1
Question 1.
The following graph shows the temperature of a patient in a hospital, recorded every hour.
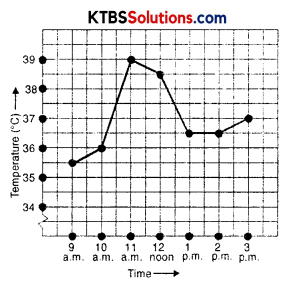
(a) What was the patient’s temperature at 1 p.m.?
(b) When was the patient’s temperature 38.5° C?
(c) The patient’s temperature was the same two times during the period given. What were these two times?
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
(e) During which periods did the patient’s temperature showed an upward trend?
Solution:
(a) The patient’s temperature at 1 p.m is 36.5°C.
(b) 12 noon.
(c) At 1 p.m and 2 p.m.
(d) The temperature at 1.30 p.m was 36.5°C. The point between 1 p.m. and 2 p.m. on X-axis is equidistance from the two points showing 1 p.m. and 2 p.m., so it will represent 1.30 p.m. Similarly, the point on the Y-axis, between 36°C and 37°C will represent 36.5°C.
(e) 9 a.m to 11 a.m.
![]()
Question 2.
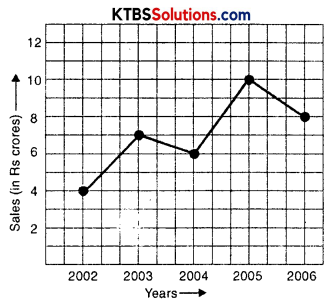
The following line graph shows the yearly sales figures for a manufacturing company.
(а) What were the sales in (i) 2002 (ii) 2006?
(b) What were the sales in (i) 2003 (ii) 2005?
(c) Compute the difference between the sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year?
Solution:
(a) (i) Sales in 2002 is 4 crorers.
(ii) Sales in 2006 is 8 crores.
(b) (i) Sales in 2003 is 7 crores.
(ii) Sales in 2005 is 10 crores.
(c) The difference in sales of 2006 and 2002 is (8 – 4) = 4 crores.
(d) The difference in sales in 2005 and 2004 is greatest that is (10 – 4) = 6 crores.
![]()
Question 3.
For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown in the following graph.
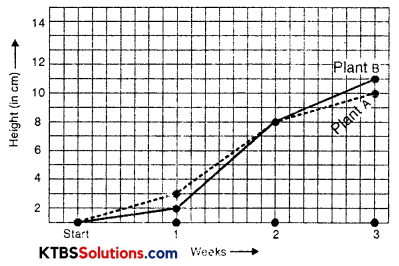
(a) How high was Plant A after (i) 2 weeks (ii) 3 weeks?
(b) How high was Plant B after (i) 2 weeks (ii) 3 weeks?
(c) How much did Plant A grow during the 3rd week?
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.
Solution:
(a) (i) Height of plant A after 2 weeks is 7 cm.
(ii) Height of plant A after 3 weeks is 9 cm.
(b) (i) Height of plant B after 2 weeks is 7 cm.
(ii) Height of plant B after 3 weeks is 10 cm.
(c) The growth of plant A during the 3rd week is (9 – 7) = 2 cm.
(d) The growth of plant B from the end of the 2nd week to the end of the 3rd week is (10 – 7) = 3 cm.
(e) During the second week plant A grew most.
(f) plant B grew most during 2nd week.
(g) At the end of the second week height of both A and B plants is the same.
![]()
Question 4.
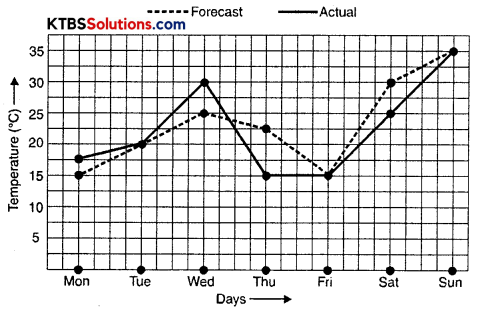
The following graph shows the temperature forecast and the actual temperature for each day of the week.
(а) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?
Solution:
(a) On Tuesday, Friday, and Sunday the forecast of temperature was the same as the actual temperature.
(b) The maximum forecast temperature during the week was 35° C.
(c) The minimum actual temperature during the week was 15° C.
(d) The difference between the actual temperature and forecast temperature was maximum on Thursday.
![]()
Question 5.
Use the tables below to draw linear graphs.
(a) The number of days a hillside city received snow in different years.

(b) Population (in thousands) of men and women in a village in different years.

Solution:
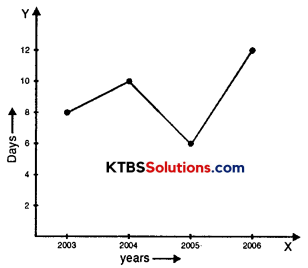
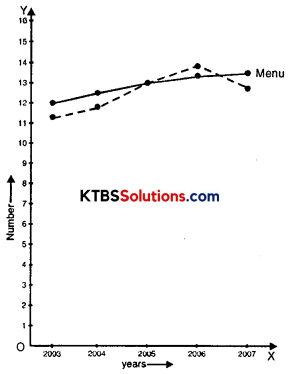
Question 6.
A courier person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(а) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?
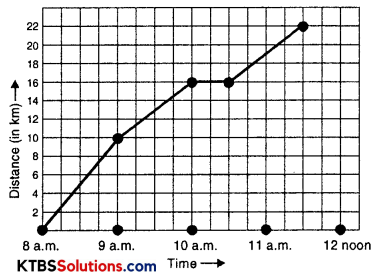
Solution:
(a) 4 small divisions = 1 hour
(b) 3 hour 30 minutes.
(c) 22 km.
(d) Yes, He stops from 10 a.m to 10.30 a.m. It is indicated by the horizontal line in the graph.
(e) He rides faster between 8 a.m and 9 a.m.
![]()
Question 7.
Can there be a time-temperature graph as follows? Justify your answer.
(i)
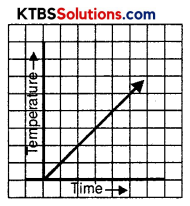
(ii)
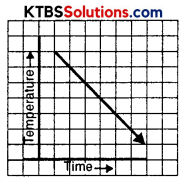
(iii)

(iv)
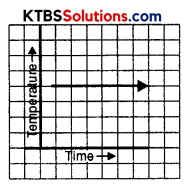
Solution:
(i) Yes, this represents a time-temperature graph. The temperature is changing with the change in time. In this case (graph) temperature is increasing.
(ii) Yes, the temperature is falling with the change in time.
(iii) No, it can’t be a time-temperature graph. Here the temperature is changing without change in time. Which is not possible.
(iv) Yes, this represents a time-temperature graph. It shows a constant temperature at different times.