KSEEB Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1

You can Download KSEEB Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1 Questions and Answers helps you to revise the complete syllabus.

KSEEB Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1

Find the values of the letters in each of the following and give reasons for the steps involved.

Question 1.

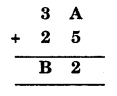
Solution:
We have

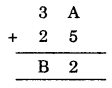
In column one A + 5, we get 2 i.e., the number whose one’s digit is 2. Thus A should be 7.

That is B = 6

Question 2.

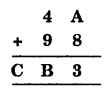
Solution:
We have

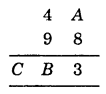
Here, A + 8 = 3 (a number whose ones digit is 3)
∴ ‘A’ should be 5

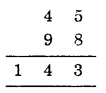
Thus A = 5, B = 4, and C = 1

Question 3.

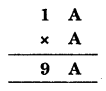
Solution:
We have

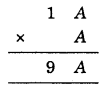
Since the ones digit of A × A = A
So, it must be 6, because the product of a number and A is 9.
i.e., 1 × A = 9 ⇒ A = 9
but A = 9 does not satisfy
So, A = 6
Now

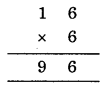
Question 4.

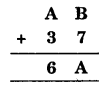
Solution:
We have

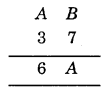
Here, B + 7 is ‘A’ that is a number whose one digit is ‘A’.
Let us put the values of B starting from 0.
If B = 0, then A = 7
∴ 7 + 6 ≠ 6
If B = 1, then A = 8
∴ 8 + 3 ≠ 6
If B = 2, then A = 9
∴ 9 + 3 ≠ 6
If B – 5, then A = 2
∴ (2 + 3) + 1 = 6

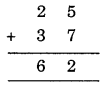
So, B = 5 and A = 2 satisfy the given condition.

Question 5.

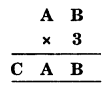
Solution:
We have

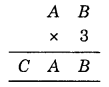
Since the one digit of B × 3 is B.
It must be B = 0 or B = 5.
Now, look at A.
If A = 1, then

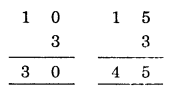
(Do not satisfy the condition)
If A = 2 then

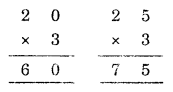
(Do not satisfy the condition)
If A = 3 then

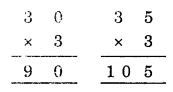
(Do not satisfy the condition)
If A = 5 then

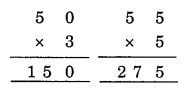
So B = 0, A = 5 and C = 1

Question 6.

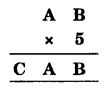
Solution:
We have

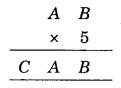
Since the one digit of B × 5 is B, B must be 0 or 5.
Now, look at A.

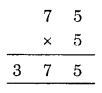
∴ A = 7, B = 5 and C = 3

Question 7.

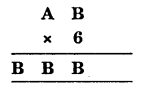
Solution:
We have

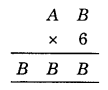
Since the one’s digit of B × 6 is 6
∴ Possible values of B are 0, 4, 6, and 8.
Now, look at A.
So, the value of B B B maybe 444, 666, or 888. [000 is not posible]
666 ÷ 6 = 111 which is a 3 digits number
888 ÷ 6 = 148 which is a 3 digits number
444 ÷ 6 = 74 which is a 2 digits number

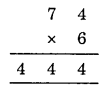
Thus B = 4 and A = 7

Question 8.

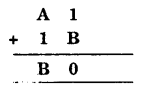
Solution:
We have

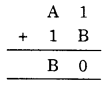
If you study the addition in the one’s column
i.e., (1 + B), you get ‘0’
∴ B should be 9.
Thus, A must be 7.

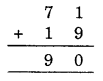
Thus, B = 9 and A = 7

Question 9.

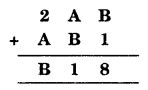
Solution:
We have

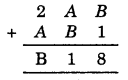
If you study the addition in the one’s column i.e., (B + 1) then you get ‘8’
∴ ‘B’ should be 7 and A should be 4.

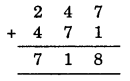
So, the given condition is satisfied.
Hence B = 7 and A = 4

Question 10.

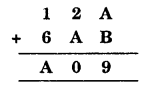
Solution:
We have

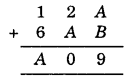
Since the addition of ones, the column gives the value 9.
∴ A + B should (1, 8) or (8, 1)
Now, let us supply hit and trial method
If A = 1 and B = 8 then

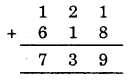
If A = 8 and B = 1 then

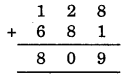
Thus A = 8 and B = 1 satisfied the given condition.