KSEEB Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals InText Questions

You can Download KSEEB Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals InText Questions Questions and Answers helps you to revise the complete syllabus.

KSEEB Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals InText Questions

Try These (Page 43)

Take a regular hexagon Fig. 3.10.

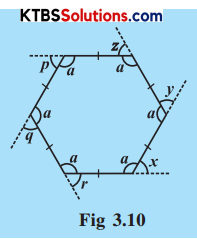
Question 1.
What is the sum of the measures of its exterior angles x, y, z, p, q, r?
Solution:
Since ∠a + ∠r = 180° (CE they form a linear pair)
Hence,
(∠a + ∠r) + (∠a + ∠x) + (∠a + ∠y) + (∠a + ∠z) + (∠a + ∠p) + (∠a + ∠q) = 180° × 6
⇒ ∠a + ∠a + ∠a + ∠a + ∠a + ∠a + ∠r + ∠x + ∠y + ∠z + ∠p + ∠q = 1080°
⇒ 6∠a + ∠r + ∠x + ∠y + ∠z + ∠p + ∠q = 1080°
⇒ 6 × 120° + ∠r + ∠x + ∠y + ∠z + ∠p + ∠q = 1080°
(∵ Interior angle of a regular hexagon is 120°)
⇒ 720° + ∠r + ∠x + ∠y + ∠z + ∠p + ∠q = 1080°
⇒ ∠r + ∠x + ∠y + ∠z + ∠p + ∠q = 1080° – 720°
⇒ ∠r + ∠x + ∠y + ∠z + ∠p + ∠q = 360°

Question 2.
Is x = y = z = p = q = r? Why?
Solution:
Yes these are equal
∠x + ∠a = ∠y + ∠a = ∠z + ∠a = ∠p + ∠a = ∠q + ∠a = 180° (Linear pair)
⇒ ∠x + ∠a = 180°
⇒ ∠x + 120° = 180°
⇒ ∠x = 180° – 120°
∴ ∠x = 60°
Similarly, ∠y = ∠z = ∠p = ∠q = 60°

Question 3.
What is the measure of each?
(i) exterior angle
(ii) interior angle
Solution:
(i) The measure of each exterior angle = \(\frac{360^{\circ}}{6}\) = 60°
(ii) The measure of each interior angle = a + 60° = 180°
∴ a = 120°

Question 4.
Repeat this activity for the cases of
(i) a regular octagon
(ii) a regular 20-gon
Solution:
(i) The exterior angle of a regular octagon = \(\frac{360^{\circ}}{8}\) = 45°
The interior angle of a regular octagon = 180° – 45° = 135°
(ii) The exterior angle of a regular 20-gon = \(\frac{360^{\circ}}{20}\) = 18°
The interior angle of a regular 20-gon = 180° – 18° = 162°

Try These (Page 47)

Question 1.
Take two identical set squares with angles 30° – 60° – 90° and place them adjacently to form a parallelogram as shown in Fig. Does this help you to verify the above property?

Solution:
Yes, it helps us to verify one of the properties of a parallelogram, that its opposite sides are equal.

Try These (Page 48)

Question 1.
Take two identical 30° – 60° – 90° set squares and form a parallelogram as before. Does the figure obtain help to confirm the property (The opposite angles of a parallelogram are of equal measure)?
Solution:
Yes, it confirms the property of a parallelogram that its opposite angles are of equal measure. Here, opposite angles are 90° each.