Students can Download Maths Chapter 4 Factorisation Additional Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 8 Maths Chapter 4 Factorisation Additional Questions
Question 1.
Choose the correct answer
(a) 4a + 12b is equal to
A. 4a
B. 12b
C. 4(a + 3b)
D. 3a
Answer:
(C) 4 (a + 3b)
![]()
(b) The product of two numbers is positive and their sum is negative only when
A. both are positive
B. both are negative
C. one positive other negative
D. one of them is equal to zero
Answer:
(B) both are negative
(c) Factorising x2 + 6x + 8 we get
A. (x + 1) (x + 8)
B. (x + 6) (x + 2)
C. (x + 10) (x – 2)
D. (x + 4) (x + 2)
Answer:
(D) (x + 4) (x + 2)
(d) The denominator of an algebraic fraction should not be
A. 1
B. 0
C. 4
D. 7
Answer:
(B) 0
(e) If the sum of two integers is – 2 and their proiduct is – 24, the numbers are
A. 6 and 4
B. – 6 and 4
C. – 6 and -4
D. 6 and – 4
Answer:
(B) – 6 and 4
(f) The difference (0.7)2 – (0.3)2 simplifies to
A. 0.4
B. 0.04
C. 0.49
D. 0.56
Answer:
(A) 0.4
![]()
Question 2.
Factorise the following
(i) x2 + 6x + 9
Answer:
x2 + 6x + 9
= x2 + 2.x.3 + 32
= (x + 3)2
(ii) 1 – 8x + 16x2
Answer:
1 – 8x + 16x2
= 12 – 2.1.4x + (4x)2
= (1 – 4x)2
(iii) 4x2 – 81y2
Answer:
4x2 – 81 y2
= (2x)2 – ( 9y)2
= (2x + 9y) (2x – 9y)
(iv) 4a2 + 4ab + b2
Answer:
4a2 + 4ab + b2
= (2a)2 +2.2a.b + b2
= (2a + b)2
(v) a2b2 + c2d2 – a2c2 – b2d2
Answer:
a2b2 + c2d2 – a2c2 – b2d2
= a2b2 – a2c2 + c2d2 – b2d2
= a2 (b2 – c2) – d2 (b2 – c2)
= (b2 – c2) (a2 – d2)
![]()

Question 3.
Factorise the following
(i) x2 + 7x + 12
Answer:
x2 + 7x + 12 12xz
x2 + 4x + 3x + 12
x (x + 4) + 3 (x + 4)
(x + 4) (x + 3)

(ii) x2 + x – 12
Answer:
x2 + 4x – 3x – 12
x(x + 4) -3 (x + 4)
(x + 4) (x – 3)

(iii) x2 – 3x – 18
Answer:
x2 – 6x + 3x – 18
x(x – 6) +3 (x -6)
(x – 6) (x + 3)

(iv) x2 + 4x – 21
Answer:
x2 + 7x – 3x – 12
x(x + 7) -3 (x + 7)
(x + 7) (x – 3)

(v) x2 – 4x – 192
Answer:
x2 – 16x + 12x – 192
x(x – 16) +12 (x – 16)
(x -16) (x +12)

(vi) x4 – 5x2 + 4
Answer:
x4 – 4x2 – x2 + 4
x2(x2 – 4) -1 (x2 – 4)
(x2 – 4) (x2 – 1) = (x + 2) (x – 2)
(x + 1) (x – 1)

(vii) x4 – 13x2y2 + 36y4
Answer:
x4 -9x2y2 – 4x2y2 +36y4
x2(x2 – 9y2) -4y2
(x2 – 9y2)
(x2 – 9y2) (x2 – 4y2)
= [x2 – (3y)2] [x2 – (2y)2]
= (x + 3y) (x – 3y) (x + 2y) (x – 2y)

Question 4.
Factorise the following
(i) 2x2 + 7x + 6
Answer:
2x2 + 4x + 3x + 6
2x (x +2) + 3 (x + 2)
(x + 2) (2x + 3)
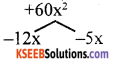
(ii) 3x2 – 17x + 20
Answer:
3x2 – 12x – 5x + 20
3x (x – 4) – 5 (x – 4)
(x – 4) (3x – 5)
(iii) 6x2 – 5x – 14
Answer:
6x2 – 12x + 7x – 14
6x (x – 2) + 7 (x – 2)
(x – 2) (6x +7)

(iv) 4x2 + 12xy – 5y2
Answer:
4x2 – lOxy + 2xy + 5y2 – 20x2y2
2x (2x + 5y) + y
(2x + 5y)
(2x + 5y) (2x + y)

(v) 4x4 – 5x2 + 1
Answer:
4x2 – 4x2 – x2 + 1 4×4
4x2 (x2 – 1) – 1
(x2 – 1)
(x2 – 1) (4x2 – 1)
(x2 – 12) – ((2x)2 – 12)
(x2 – l2) – ((2x)2 – l2)
(x + 1) (x – 1) (2x + 1) (2x – 1)

![]()
Question 5.
Factorise the following
(i) x8 – y8
Answer:
(x4)2 – (y4)2
= (x4 + y4) (x4 – y4)
= (x4 + y4) [(x2)2 – (y2)2]
= (x4 + y4) (x2 + y2) (x2 – y2)
= (x4 + y4) (x2 + y2) (x + y)
(x – y)
(ii) a12x4 – a4x12
Answer:
[(a6)2(x2)2 – (a2)2(x6)2]
= [(a6x2)2 – (a2x6)2]
= (a6x2 + a2x6) (a6x2 – a2x6)
= a2x2 (a4 + x4)
[(a3)2 x2 – a2 (x3)2]
= a2x2 (a4 + x4) [(a3x)2 – (ax3)2] = a2x2 (a4 + x4) [(a3x + ax3)
(a3x – ax3)]
= a2x2 (a4 + x4) [ax(a2 + x2).ax (a2 – x2)]
= a2x2 (a4 + x4) [a2x2 (a2 + x2) (a2 – x2)]
= a4x4 (a4 + x4) (a2 + x2) (a + x) (a – x)
(iii) x4 + x2 + 1
Answer:
X4 + X2 + 1 + X2 – X2
= x4 + 2x2 + 1 – x2
= (x2)2 + 2.x2.1 + l2 – x2
= (x2 + l)2 – X2
= (x2 + 1 + x) (x2 + 1 – x)
= (x2 + x + 1) (x2 – X + 1)
(iv) x4 + 5x2 + 9
Answer:
x4 + 5x2 + 9 + x2 – x2
= x4 + 6x2 + 9 – x2
= (x2)2 + 2.x2.3 + 32 – x2 = (x2 + 3)2 – x2
= (x2 + 3 + x) (x2 + 3 – x)
= (x2 + x + 3) (x2 – x + 3)
![]()
Question 6.
Factorise x4 + 4y4 use this to prove that 2011 4 + 64 is a composite number Answer:
x4 + 4y4
= (x2)2 + (2y2)2
= (x2 + 2y2)2 – 2x2.2y2
[v a2 + b2 = (a + b)2 – 2ab]
= (x2 + 2y2) – (4x2y2)
= (x2 + 2y2) – (2xy)2
(x2 + 2y2 + 2xy) (x2 + 2y2 – 2xy) [a2 – b2 = (a + b) (a – b)]
∴ x4 + 4y4 = (x2 + 2y2 + 2xy)
(x2 + 2y2 – 2xy)
Similarly 20114 + 64 can be written as
20114 + 4 x 16 = (2011)4 + 4.24
= (20112 + 2.22 + 2.2011.2) (20112 + 2.22 – 2.2011.2)
∴ 20114 + 64 is a composite number.
![]()