1st PUC Basic Maths Question Bank Chapter 13 Angles and Trigonometric Ratios

Students can Download Basic Maths Chapter 13 Angles and Trigonometric Ratios Questions and Answers, Notes Pdf, 1st PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 1st PUC Basic Maths Question Bank Chapter 13 Angles and Trigonometric Ratios

Question 1.
Find the length of the arc and the area of the sector formed by an arc of a circle of radius 8 cm subtending an angle 25° as the centre.
Answer:

Question 2.
Find the angle between minute hand and the hourhand of a clock when the time is 5.40.
Answer:
Angle described by the hourhand is 12 hours = 360°
∴ per hour = \(\frac{360}{12}\) = 30°

Now the angle described by minute hand is 60° minutes = 360°
i.e., Angle in 40° minutes = 40 × 6° = 240°,

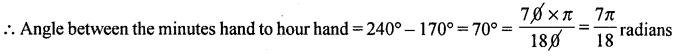
Question 3.
A circular wire of radius 6 cm is cut and bent so as to lie along the circumference of a loop whose radius in 66 cm. Find in degrees the angle which subtended at the centre of the loop.
Answer:
The length of the arc subtended is the circumference of the circle of radius 6cm.
∴ S = 2πr = 2π × 6 = 127 cm
radius of the loop = 66cm

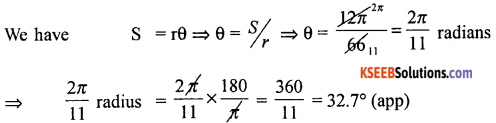
Question 4.
The angles of a triangle are in A.P and the greatest is double the least. Express the angles in degrees and radians.
Answer:
Let the angle, be (a – d)° a° and (a + d)°, (a > d > 0°)
∴ (a – d) + a + (a + d) = 180° ⇒ 3a = 180° ⇒ a = 60°
i. e., (a – d) is the least and (a + d) is the greatest,
given (a + d) = 2 (a – d) = a + d = 2a – 2d
⇒ a – 3d = 0 ⇒ 60° – 3d = 0 ⇒ d = 20°

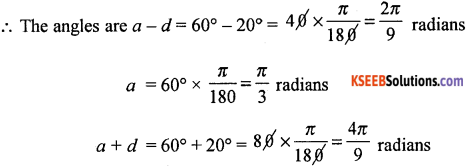
Question 5.
Express 25°. 30′ 10″ in radians.
Answer:

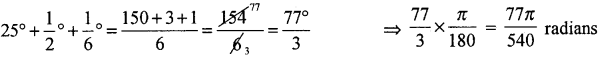
Trigonometric Ratios of Acute Angle

Question 1.
Prove that tan α\(\sqrt{1-\sin ^{2} \alpha}\) = sin α
Answer:
LHS : tan α . \(\sqrt{1-\sin ^{2} \alpha}\) = tan α . \(\sqrt{\cos ^{2} \alpha}\)
= \(\frac{\sin \alpha}{\cos \alpha}\) × cos α = sin α = RHS

Question 2.
Prove that \(\frac{1-\cos \theta}{\sin \theta}=\frac{\sin \theta}{1+\cos \theta}\)
Answer:

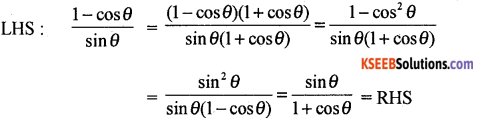
Question 3.
Prove that \(\sqrt{\frac{1-\sin A}{1+\sin A}}\) = sec A – tan A.
Answer:

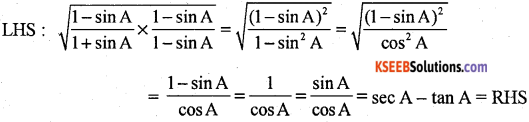
Question 4.
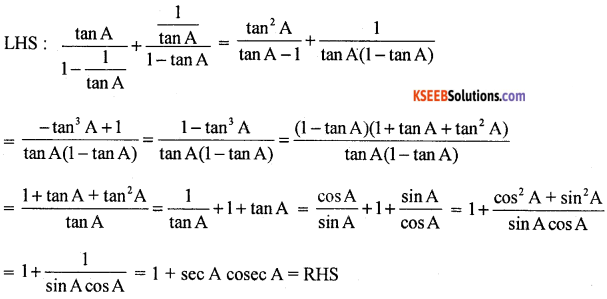
Show that \(\frac{\tan A}{1-\cot A}+\frac{\cot A}{1-\tan A}\) = 1 + sec A cosec A.
Answer:

Question 5.
If x = a cos θ + sin θ. y = a sin θ – b cos θ. Show that x² + y² = a² + b²
Answer:
Consider x² = (a cos θ + b sin θ)²
⇒ x² = a²cos²θ + 2ab cos θ sin θ + b² sin²θ …….(1)
Again consider
y² = (a sin θ – b cos θ)² => y² = a² sin²θ – ab cos θ sin θ + b² cos² θ …….. (2)
(1) + (2) ⇒ x² + y² = a² + b²

Question 6.
If sin θ = \(\frac{3}{5}\) and θ is acute, find the value of
Answer:
By data sin θ = \(\frac{3}{5}\)
cos θ = \(\frac{3}{5}\) . tan θ = \(\frac{3}{4}\), cot = \(\frac{4}{3}\)

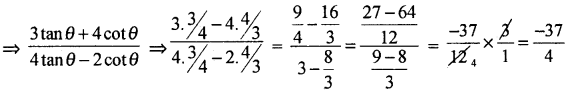
Trigonometric Ratios of some Standard Angles

Question 1.
Find the value of cos \(\frac{\pi}{3}\) – sin \(\frac{\pi}{6}\) – tan³ \(\frac{\pi}{4}\)
Answer:

Question 2.
Find value of 3 tan²30° + \(\frac{4}{3}\)sin²60° – \(\frac{1}{2}\)cosec²30° – \(\frac{1}{3}\)cos² 45°
Answer:

Question 3.
Find x, if \(\frac{x \csc ^{2} 30^{\circ} \cdot \sec ^{2} 45^{\circ}}{6 \cos ^{2} 45^{\circ} \sin 30^{\circ}}\) = tan² 45° – tan² 60°
Answer:

Question 4.
Show that cos² \(\frac{\pi}{4}\) – cos⁴ \(\frac{\pi}{6}\) + sin⁴ \(\frac{\pi}{6}\) + sin⁴ \(\frac{\pi}{3}\) = \(\frac{9}{16}\)
Answer:

Question 5.

Answer:

Heights and Distances

Question 1.
A person is at the top of tower 75 feet high from there he observes a vertical pole and finds the angles of depression of the top and the bottom of the pole which are 30° and 60° respectively. Find the height of the pole.
Answer:
Let AB be the tower = 75 feet,
CD be the pole = x
AX is ∥^lel to MC
∴ AĈM = XÂC = 30°
AX ∥^lel BD
Hence AD̂B = XÂD = 60°

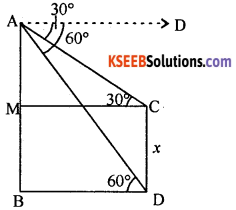
Now from the right triangle ADB, we have
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ BD = \(\frac{\mathrm{AB}}{\tan 60^{\circ}}\) = BD = \(\frac{75}{\sqrt{3}}\)
tan 30° = \(\frac{\mathrm{AM}}{\mathrm{MC}}\)
⇒ AM = MC . tan 30°
⇒ AM = BD \(\frac{1}{\sqrt{3}}=\frac{75}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}\) = 25
Now x = CD = MB
⇒ x = AB – AM = 75 – 25 = 50 feet

Question 2.
A person standing on the bank of a river observe that the angle of elevation of the top of a tree on the opposite bank is 60°, when he returns 60 feet from the bank, he finds the angle to be 30°. Find the height of the tree and breadth of the river.
Answer:
PQ represent tree A and B be the points of observation. BQ is the breadth of the river. From the figure

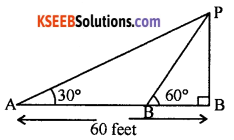
tan 60° = \(\frac{P Q}{B Q}\)
⇒ PQ = BQ . √3
Again from the figure we have
tan 30° = \(\frac{P Q}{A Q}\)
⇒ AQ = \(\frac{P Q}{\tan 30^{\circ}}\) = AQ = √3PQ
⇒ AQ = √3 . (√3BQ) = 3BQ. Now BQ ⇒ AQ – AB
⇒ BQ = 3BQ – AB
⇒ 2BQ = 60
∴ BQ = 30° is the breadth of the river
∴ height of the tree = PQ = √3.BQ = √3.30 = 30√3

Question 3.
The angle of elevation of a stationary cloud from a point 3000 cm above the lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake.
Answer:
D – the image of the cloud C.
AB the surface of the lake
Also CB = BD
Let P be the position of observation.
Thus by data AP = 3000 cm
By data, EP̂C = 30°, EP̂D = 60°


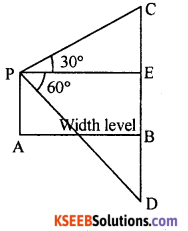
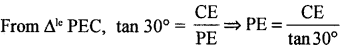
⇒ PE = √3 . CE ….. (1)

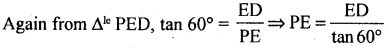
⇒ PE = \(\frac{\mathrm{ED}}{\sqrt{3}}\) ….. (2)
From (1) and (2) we get
⇒ √3CE = \(\frac{1}{\sqrt{3}}\)ED = 3CE = ED
⇒ 3(BC – BE) = EB + BD
⇒ 3(BC – 3000) = 3000 + BC (∵ BD = BC and BE PA = 3000)
⇒ 3BC – 9000 = 3000 + BC
⇒ 2BC = 12,000 = BC = 6000 cm
∴ height of the cloud = 600 cms