You can Download Chapter 5 States of Matter Questions and Answers, Notes, 1st PUC Chemistry Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Chemistry Question Bank Chapter 5 States of Matter
1st PUC Chemistry States of Matter One Mark Questions and Answers
Question 1.
Write the ideal gas equation for one mole of a gas.
Answer:
PV = RT
Question 2.
Write the Vander Waals1 equation for one mole of a real gas.
Answer:

Question 3.
Write Vander Waals equation constants ‘a’ and ‘b’.
Answer:
Units for ‘a’: L2 atm mol-2
Units for ‘b’: Litre mole-1
Question 4.
Gie the value of universal gas constant in SI units.
Answer:
8.3124 J K-1 mol-1
Question 5.
Give the combined gas equation (or general equation for gases).
Answer:
PV = nRT for n moles.
![]()
Question 6.
Write kinetic equation for gases.
Answer:
PV = \(\frac { 1 }{ 3 }\) mnc2
Question 7.
Write an equation for the pressure exerted by a gas in a container.
Answer:
\(\mathrm{PV}=\frac{1}{3} \frac{\mathrm{mnc}^{2}}{\mathrm{V}}\)
Question 8.
Write an equation for the root mean square velocity of a gas.
Answer:
\(V_{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}\)
Question 9.
Liquid ammonia bottle is cooled before opening the seal. Why?
Answer:
NH3 is liquified at high temperature and pressure. It is cooled so as to reduce temperature so that it does not burst.
Question 10.
The size of weather balloon becomes larger and larger as it ascends up into higher altitudes. Why?
Answer:
At higher altitudes, atmospheric condition is less, therefore, air inside balloon exerts less pressure released and it becomes larger and larger.
Question 11.
Which property of liquid is responsible for spherical shape of liquid drops?
Answer:
Surface tension and viscosity.
![]()
Question 12.
What is the effect of temperature on viscosity and why?
Answer:
Viscosity decrease in the temperature because intermolecular force of attraction decreases.
Question 13.
What is the effect of pressure on (i) viscosity, (ii) surface tension, (iii) density of liquid? –
Answer:
Increase in pressure increases viscosity, surface tension and density because inter molecular force of attraction increases.
Question 14.
What is the boiling point of water at (i) higher altitudes, (ii) in pressure cooker?
Answer:
(i) >100 °C (ii) < 100 °C.
Question 15.
Name four measurable properties of gases.
Answer:
- Volume
- Pressure
- Temperature
- Mass
Question 16.
Name the SI unit of pressure and give its definition.
Answer:
Pascal is SI unit of pressure. It is defined as pressure exerted when 1 newton force is acting per square metre area.
![]()
Question 17.
Define an ideal gas.
Answer:
Ideal gas is gas which follows all the gas laws at all temperature and pressure.
Question 18.
Give various forms of ideal gas equation.
Answer:
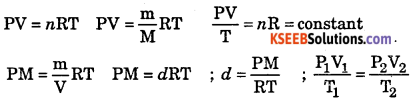
Question 19.
What are real gases?
Answer:
Real gases are those which do not follow all the gas laws at all temperature and
pressure.
Question 20.
Under what conditions of T and P, most of gases deviate from ideal gas behavior?
Answer:
At low temperature and high pressure most of gases deviate from ideal gas behavior.
Question 21.
State Dalton’s law of partial pressure.
Answer:
It states that whenever two or more gases, which do not react chemically, are
enclosed in vessel, the total pressure is equal to sum of partial pressure of each gas.
Question 22.
What is meant by compressibility factor?
Answer:
Compressibility factor is ratio of PV to nRT.
Z = \(\frac{\mathrm{PV}}{n \mathrm{RT}}b\)
Question 23.
Define boiling point of a liquid.
Answer:
Boiling point is temperature at which vapour pressure of liquid becomes equal to atmospheric pressure.
Question 24.
How is density of gas related to its molar mass?
Answer:
Density of gas is directly proportional to molar mass.
![]()
Question 25.
How is molar mass of gas related to rate of diffusion?
Answer:
The rate of diffusion is inversely proportional to molecular mass
\(\frac{r_{1}}{r_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}\)
Question 26.
What is meant by elastic collision?
Answer:
Elastic collision is a collision in which there is no net loss energy rather there is transfer of energy.
Question 27.
Define aqueous tension.
Answer:
Aqueous tension is pressure of water vapour at particular temperature.
Question 28.
State Graham’s law of diffusion.
Answer:
It states that the rate of diffusion of gases is inversely proportional to square root of molecular masses at constant temperature and pressure.
Question 29.
Define “effusion”.
Answer:
Effusion is the process of diffusion taking place from a tiny hole.
Question 30.
Arrange the following gases in the increasing orderof their van der waals1 constant ‘a’ values : CO2, H2> C6H6
Answer:
H2 < CO2 < C6H6
Question 31.
What is SI unit of (i) viscosity, (ii) surface tension?
Answer:
(i) Pascal second, (ii) Nm1
Question 32.
Define critical temperature of the gas. Give its expression.
Answer:
Critical temperature is a temperature above which a gas cannot be liquefied.
\(\mathrm{T}_{\mathrm{c}}=\frac{8 \mathrm{a}}{27 b \mathrm{R}}\) where ‘a’ and ‘b’ are Van der waal’s constants, R is gas constant.
![]()
Question 33.
What do you mean by Boyle temperature? Give its expression and its relation with inversion temperature.
Answer:
Boyle temperature is a temperature at which most of real gases show ideal gas behavior over wide range of pressure. \(\mathrm{T}_{b}=\frac{\mathrm{a}}{b \mathrm{R}} \mathrm{T}_{\mathrm{i}}=2 \mathrm{T}_{b}\)
Question 34.
Define inversion temperature of a gas.
Answer:
Inversion temperature is a temperature below which if gas is allowed to expand, it causes cooling effect.
Question 35.
Define (i) critical pressure, (ii) critical volume and give their expression.
Answer:
(i) Critical pressure, it is pressure required to liquefy the gas at critical temperature.
\(\mathrm{P}_{\mathrm{c}}=\frac{\mathrm{a}}{27 \mathrm{b}^{2}}\)
(ii) Critical volume, it is volume occupied by 1 mole of gas at critical temperature and pressure. Vc = 3b
Question 36.
What type of graph will you get when PV is plotted against P at constant temperature.
Answer:
A straight line parallel to pressure axis.
1st PUC Chemistry States of Matter Two Marks Questions and Answers
Question 1.
State Boyle’s law of gases. Give its mathematical expression.
Answer:
Boyle’s law states volume of fixed mass of gas in inversely proportional to pressure at constant temperature. (P1V1 = P(2V2)T
Question 2.
State Charle’s law. Give the mathematical expression.
Answer:
Charle’s law states that volume of fixed mass of gas is directly proportional to absolute temperature at constant pressure.
\(\left(\frac{\mathrm{V}_{1}}{\mathrm{T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{T}_{2}}\right)_{\mathrm{P}}\)
![]()
Question 3.
Give any two differences between ideal and real gas.
Answer:

Question 4.
Mention the causes for the deviation of real gas from ideal behaviour.
Answer:
- There is no intermolecular force of attraction within gaseous molecules (at high pressure and low temperature there is appreciable intermolecular force of attraction).
- The actual volume of the molecule is negligible as compared to total volume of the gas. (At high pressure the gaseous molecule occupy minimum volume, which is not negligible).
Note: Because of this deviation Van der waal modified the ideal gas pressure and ideal gas volume respectively.
Question 5.
What will be the density of CO2 in kg/m3 at 323 K and 101.3 kPa pressure?
Answer:
T = 323 K, P = 101.3 kPa, M = 44 × 10-3kg mol-1, d = ?,
R= 8.314 × 10-3 kPa m3K-1mol-1
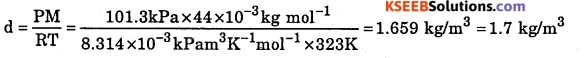
Question 6.
How many molecules of an ideal gas are there in 1 × 10-3 dm3 at STP?
Answer:
22.4 dm3 of an ideal gas has 6.023 × 1023 molecules at STP
1 × l0-3dm3 of an ideal gas contains = \(\frac{6.023 \times 10^{23}}{22.4} \times 1 \times 10^{-3}=2.69 \times 10^{19}\)molecules.
Question 7.
Calculate the number of moles of hydrogen present in 500 cm3 of a gas under a pressure of 101.3 kPa at a temperature of 300 K. (R = 8.314 J K-1 mol-1).
Answer:
n = ?

Question 8.
50 ml of oxygen were collected at 100 C under 750 mm pressure. Calculate volume at STP.
Answer:
V1 = 50ml V2=?
P1= 750mm P2 = 760mm
T1 =10 + 273 = 283K T2 =273.15K

![]()
Question 9.
Why ethyl alcohol has lower boiling point than water?
Answer:
Ethyl alcohol has higher vapour pressure than water due to less intermolecular forces of attraction.
Question 10.
A human adult breathes in approximately 0.50 L of air at 1 atm with each breath. If an air tank holds 10 L of air at 200 atm, how many breaths the tank will supply?
Answer:
P1V1=P2V2
200 × 10 = 1 × V2
V2 = 2000 L
Number of Breaths = \(\frac{2000 \mathrm{L}}{0.5 \mathrm{L}}\) = 4000
Question 11.
What will happen to volume of fixed amount of gas at a certain T and P if :
(a) T is kept constant but pressure is decreased to \(\frac { 1 }{ 4 }\) th of original value?
(b) Pressure is halved and temperature in Kelvin is doubled?
Answer:
(a) The volume will become 4 times
(b) The volume will remain same
Question 12.
10 g of O2 were introduced into an evacuated vessel of 5 L capacity at 27 °C,
Calculate pressure of gas in bar in the container [R = 0.083 bar L K-1 mol -1] [At. mass of O = 16u]
Answer:
PV = raRT bar
P × 5 L = \(\frac { 10 }{ 32 }\) × 0.083 × 300 K
P = \(\frac{24.9 \times 10}{160}=\frac{249}{160}\) = 1.556 bar
Question 13.
Calculate the density of Rn gas at 298 K and 755 mm Hg pressure. [Atomic mass of Rn = 222u]
Answer:
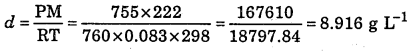
Question 14.
2NO (g) + O2 (g) → 2NO2 (g). A 1.98 L reaction vessel is filled with a mixture of NO and O2 to a pressure of 4.33 bar at 310 K. The reaction is allowed to continue until the total pressure decreases to 4.00 bar. What is the final pressure of NO2 ?
Answer:
Reaction 2NO + O2 → 2NO2
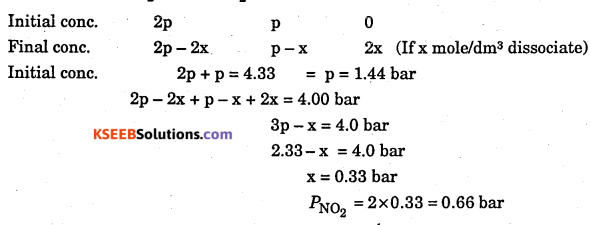
Question 15.
Calculate the total pressure in a 10 L cylinder which contains 0.4 g of helium, 1.6 g of oxygen and 1.4 g of nitrogen at 27 °C. Also calculate the partial pressure of helium gas in the cylinder. Assume ideal behaviour for gases.
Ans:
Total number of moles = \(\frac{0.4}{4}+\frac{1.6}{32}+\frac{1.4}{28}\) = 0.1 + 0.05 + 0.05 =0.2 moles.
pV = nRT
p × 10 L = 0.2 × 0.082 × 300 ⇒ p = \(\frac{24.6 \times 0.2}{10}\)
p = 0.492 atm
PHe = \(\frac{0.1}{0.2}\) × 0.492 = 0.246 atm
![]()
Question 16.
Calculate the number of moles of hydrogen (H2) present in a 500 cm3 sample of hydrogen gas at a pressure of 760 mm Hg and 27 °C.
Answer:
PV = nRT, P = 1 atm, V = 500 cm3, n = ?, R = 82.1 atm cm3K-1mol-1, T = 300 K.
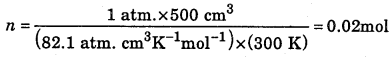
Question 17.
34.05 ml of phosphorus vapour weighs 0.0625 g at 0.1 bar pressure. What is the molar mass of phosphorus?
Answer:
pV = nRT

Question 18.
In terms of Charle’s law explain why -273 °C is the lowest possible temperature.
Answer:
Charles Law plotted graphically with volume against temperature in °C. These plots when extended intersect the temperature axis at the same point -273 °C. Charles concluded that all gases at this temperature could have zero volume and below this temperature volume would be negative. It shows -273 °C is lowest temperature attainable.
Question 19.
(i) Why is Boyle’s law is obeyed by N2,O2 or CO2 only at low pressure and high temperature?
(ii) Compare the rate of diffusion of HCl and NH3. (Atomic masses of H = 1u, Cl = 35.5 u, N = 14u)
Answer:
(i) It is because at low pressure and high temperature these gases follow ideal gas behavior due to negligible force of attraction and volume occupied by gas molecules can be ignored.
(ii)
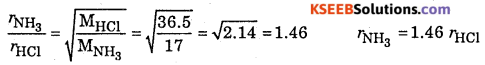
Question 20.
Arrange solid, liquid and gas in order of energy giving reasons.
Answer:
Solid<liquid
Question 21.
The Van der Waal’s constants for two gases are as follows:-

Which of them is more easily liquefiable and which has greater molecular size?
Answer:
Greater the value of ‘a’, more easily the gas is liquefiable. Similarly, greater the value of V, greater is the molecular size. Hence, gas Y will be more easily liquefiable and will have greater molecular size.
![]()
Question 22.
Compare the rates of diffusion of 235UF6 and 238UF6
Answer:
Molecular mass of 235UF6 = 235 + 6 × 19 = 349
Molecular mass of 238UF6 = 238 + 6 × 19 = 352

Question 23.
At a certain altitude, the density of air is 1/10 th of the density of the earth’s atmosphere and temperature is -10 °C. What is the pressure at that altitude? Assume that air behaves like an ideal gas, has uniform composition and is at STP at the earth’s surface.
Answer:
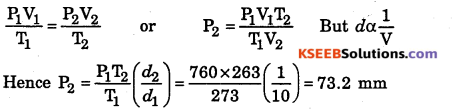
Question 24.
What is the ratio of average kinetic energy of oxygen molecules to that of ozone molecules at 27 °C?
Answer:
Average kinetic energy of any gas depends only on temperature and not upon the nature of the gas. Hence, both the gases will have same average kinetic energy at 27 °C, ie., the ratio will be 1: 1.
Question 25.
What is the difference between total kinetic energy and translational kinetic energy? For what type of molecules, the two are equal?
Answer:
Total kinetic energy is the sum of translational, vibrational and rotational kinetic energies. The total kinetic energy is equal to the translational kinetic energy for monoatomic gases (He, Ne, etc.,) as they do not possess vibrational and rotational motion but have only translation motion.
Question 26.
Out of N2 and NH3, which one will have greater value of ‘a’ and which one will have greater value of ‘b’ ?
Answer:
- As NH3 is more easily liquefiable (due to hydrogen bonding), intermolecular forces of attraction are stronger then in N2. Hence, NH3 will have greater value of‘a’.
- As NH3 molecule is larger in size than N2 , hence NH3 will have greater value for ‘b’.
(For NH3, a = 4.17 L2 atm mol-2 , b = 0.0371 L mol-1
For N2 , a = 1.39 L2 atm mol-2, b = 0.0319 L mol-1)
![]()
Question 27.
What would have happened to the gas if the molecular collisions were not elastic?
Answer:
On every collision, there would have been loss of energy. As a result, the molecules would have slowed down and ultimately settle down’ in the vessel. Moreover, the pressure would have gradually reduced to zero.
Question 28.
CO2 is heavier than O2 and N2 gases present in the air but it does not form the lower layer of the atmosphere. Why?
Answer:
Gases possess the property of diffusion which is independent of the force of gravitation. Due to diffusion, the gases mix into each other and remain almost uniformly distributed in the atmosphere.
Question 29.
N2O and CO2 have the same rate of diffusion under same conditions of temperature and pressure. Why?
Answer:
Both have same molar mass (= 44 g mol-1). According to Graham’s law of diffusion, rates of diffusion of different gases are inversely proportional to the square root of their molar masses under same conditions of temperature and pressure.
Question 30.
Why liquids have a definite volume but no definite shape?
Answer:
This is because the intermolecular forces of attraction are strong enough to hold the molecules together but not so strong as to fix them into definite positions (as in solids). Instead, they possess fluidity and hence no definite shape.
Question 31.
At a particular temperature, why vapour pressure of acetone is less than that of ether?
Answer:
This is because the intermolecular forces of attraction in acetone are stronger than those present in ether.
Question 32.
A liquid is transferred from a smaller vessel to a bigger vessel at the same temperature. What will be the effect on the vapour pressure?
Answer:
No effect, as it depends only on the nature of the liquid and temperature.
![]()
Question 33.
Why vegetables are cooked with difficulty at a hill station?
Answer:
The atmospheric pressure is less and so the boiling point is lowered.
Question 34.
What is the approximate relationship between heat of vaporization and boiling point of a liquid?
Answer:
∆Hvap / Tb =21 cal K-1 mol-1 (Trouton’s rule)
Question 35.
Explain Pressure coefficient of a gas.
Answer:
Pressure coefficient (αp). At constant volume, the increase in the pressure of a gas per degree rise of temperature divided by its pressure at 0 °C is called pressure coefficient of the gas. Mathematically, \(\alpha_{\mathrm{P}}=\frac{\mathrm{P}_{\mathrm{t}}-\mathrm{P}_{0}}{\mathrm{P}_{0} \times \mathrm{t}}\). For all gases, value of aP is αp is \(\frac { 1 }{ 273 }\)
![]()
Question 36.
Explain Atmolysis.
Answer:
Atmolysis is the process of separation of two gases on the basis of their different rates of diffusion due to difference in their densities is called atmolysis. It has been applied with success for the separation of isotopes and other gaseous mixtures.
Question 37.
Write any two difference between evaporation and boiling.
Answer:

Question 38.
Define surface tension.
Answer:
Surface tension is defined as force per unit length acting perpendicular to the tangential line on the surface. It is due to imbalanced attractive forces acting downwards and tends to reduce the surface area of a liquid to minimum.
Question 39.
Define viscosity of a liquid.
Answer:
The internal resistance to the flow of the liquids which one layer offers to another layer trying to pass over is called its viscosity. It depends upon the nature of the liquid and temperature.
![]()
Question 40.
Write an expression for kinetic gas equation.
Answer:
PV = \(\frac { 1 }{ 3 }\)mnc2
Question 41.
Both N2O and CO2 have similar rates of diffusion under similar conditions of temperature and pressure. Explain.
Answer:
Gram molar mass of both these gases is the same (44 g). According to Graham’s law of diffusion, the rates of diffusion of the gases are inversely proportional to the square root of their molar masses under similar conditions of temperature and pressure. Therefore, both these gases diffuse at the same rate.
Question 42.
If the density of a gas at the sea level at 0 °C is 1.29 kg mm-3. What is its molar mass? (Pressure = 1 bar)
Answer:
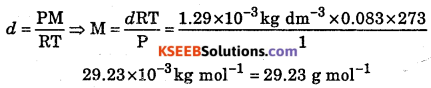
Question 43.
What will be the minimum pressure required to compress 500 dm3 of air at 1 bar to 200 dm3 at 30 °C.
Answer:
P1V1 = P2V2
1 × 500 = P2 × 200 P2 = 2.5 bar
Question 44.
Calculate the molar mass of an unknown gas which diffuses 1.117 times faster than oxygen gas through the same aperture under the same conditions of temperature and pressure.
Answer:
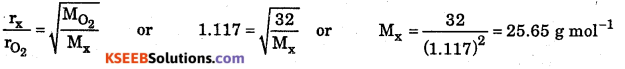
1st PUC Chemistry States of Matter Three Marks Questions and Answers
Question 1.
How vapour pressure of liquid is related to (i) temperature, (ii) nature of liquid, (iii) boiling point, (iv) atmospheric pressure?
Answer:
(i) Vapour pressure is directly proportional to temperature.
(ii) If intermolecular force of attraction is less in the liquid, its vapour pressure will be high.
(iii) Higher the vapour pressure, lower will be boiling point.
(iv) If atmospheric pressure is low, boiling point will be less and higher will be the vapour pressure.
Question 2.
Which type of intermolecular forces exist among the following molecules?
(i) H2S molecules (ii) H2O molecules (iii) Cl2 and CCl4 molecules (iv) SiH4 molecules (v) Helium atoms (vi) He atoms and HCl molecules.
Answer:
(i) Dipole-dipole interactions (because H2S is polar)
(ii) Hydrogen bonding
(iii) London dispersion force (because both are non-polar)
(iv) London dispersion forces (because SiH4 is non-polar)
(v) London dispersion forces (because He atoms have symmetrical electron clouds)
(vi) Dipole-induced dipole forces (because HCl is polar while He atom has symmetrical r electron cloud)
![]()
Question 3.
Explain Relative humidity and percentage of humidity.
Answer:
Relative humidity is a method of expressing the extent of moisture (water vapour) present in the air. It is defined as the ratio of the partial pressure of water vapour in the air to the vapour pressure of water at that particular temperature.
![]()
Thus, if the percent relative humidity of air is 60%, it means that partical pressure of water vapour in air is 0.6 times more than the vapour pressure of water at that temperature.
Question 4.
Give a reason for the following, (i) The size of weather balloon becomes larger and larger as it ascends into higher altitudes, (ii) Tyres of automobiles are inflated to lesser pressure in summer than in winter.
Answer:
(i) As we go to higher altitudes, the atmospheric pressure decreases. Then the pressure outside the balloon decreases. To regasm equilibrium with the external pressure, the gas inside expands to decrease its pressure. Hence, the size of the balloon increases.
(ii) In summer, due to higher temperature, the average kinetic energy of the air molecules inside the tyre increases, ie., molecules start moving faster. Hence, the pressure on the walls of the tube increases. Its pressure inside is not kept low at the time of inflation, at higher temperature, the pressure may become so high that the tyre may burst.
Question 5.
The molecular speeds of gaseous molecules are analogous to those of rifle bullets. Then why is the odour of a gas not detected so fast?
Answer:
Though the molecules of a gas travel at high speeds but they do not travel in straight lines in one direction like bullets. As they travel, they collide with the molecules of the gases present in the air. As a result, they are deflected. Thus, they follow a zig-zag path, i.e., the net distance travelled in a particular direction is quite small in a given time. That is why the odour is not detected so fast.
Question 6.
The average kinetic energy of a gas molecule at 0 °C is 5.621 × 10-27 J. Calculate Boltzmann constant. Also calculate the number of molecules present in one mole of the gas.
Answer:

1st PUC Chemistry States of Matter Four / Five Marks Questions and Answers
Question 1.
Write the postulates of Kinetic theory of gases.
Answer:
- Gases are made up of large number of the minute particles.
- Pressure is exerted by a gas
- There is no loss of kinetic energy.
- Molecules of gas attract on one another.
- Kinetic energy of the molecule in directly proportional to absolute temperature.
- Actual volume of the gaseous molecule very small.
- Gaseous molecules are at always in motion.
- There is more influence of gravity on movement of gaseous molecule.
Question 2.
Derive the expression for the pressure exerted by gas (Derive the Kinetic gas
equation PV = \(\frac { 1 }{ 3 }\) mn2)
Answer:
Step 1 :
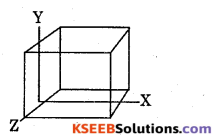
Let the mass of each molecule of gas be ‘m’ kg and all are moving with root mean square velocity ‘c’.
Step 2 :
All gaseous molecules move in all direction randomly. Hence at a given
interval of time \(\frac { n }{ 3 }\) molecules moves either along X or Y or Z axis.
Step 3 :
Consider n number of molecules of gas in a cube of length T within a 3 dimensional (X, Y and Z axis) network.
Then the area of the cube = l2 ……………..(1)
The volume of the cube = V = l3 ……………..(2)
Step 4 :
Calculation of change in momentum w.r.t. one axis.
Consider the side ‘A’ of the cube. Let one (n = 1) molecule of a gas moving along the axis towards the side ‘A’ with a velocity ‘c’ and strikes the wall ‘A’.
Initial momentum before striking = me ……………..(3)
Distance travelled = 1 units ……………..(4)
After striking the’wall ‘A’ molecule rebounds back with same speed in opposite direction.
∴ Final momentum after striking = -me ……………..(5)
Distance travelled = 1 units ……………..(6)
∴ Total change in momentum = (3) – (5) = mc – (- mc) = 2mc
Total distance travelled = (4) + (6) = 1 + 1 = 2l
Number of collisions per sec = C/21 ……………..(7)
∴ Total change in momentum per sec per molecule on face
‘A’ = collision per second × change in momentum \(\frac{\mathrm{C}}{2 \mathrm{l}} \times 2 \mathrm{m} \mathrm{C}=\frac{\mathrm{m} \mathrm{C}^{2}}{1}\)
Step 5 :
Total change in momentum per sec for one molecule strikes on the wall A = \(\frac{m c^{2}}{1}\)
∴The change in momentum per sec for \(\frac { n }{ 2 }\) molecules strikes on wall A = \(\frac{n}{3} \times \frac{m c^{2}}{1}\)
= \( \frac{\mathrm{mnc}^{2}}{31}\) …………(9)
Step 6 :
The change in momentum per sec = force. And the force in gaseous molecule is only due to pressure,

Question 3.
Derivation of Vander waal’s equation
Answer:
Pressure correction (getting corrected ideal pressure)
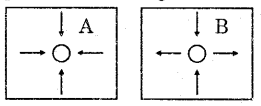
Let us consider a container containing ‘n’ number of gaseous molecule. Now consider two gaseous molecule A and B inside it.
At ‘A’ : The gaseous molecule ‘A’ present at the interior of the container and is attracted (disturbed) by all neighboring gaseous directions. Hence the net force exerted by this molecule is zero.
At ‘B’ : The gaseous molecule ‘B’ is about to strike the walls of the container, it is influenced by other neighboring molecule as follows.
(a) It is attracted by large number of molecules inward and net effect is an inward pull. This inward force (pressure) is directly proportional to the number of molecules per unit volume (at the bulk of the container) ie., P ∝ \(\frac{1}{V}\) …………(1)
(b) Within the container there are some molecules which are already striking the wall of the container. Thus there exist pulling of B inward by the molecules striking on the wall. This pressure (force) is directly proportional to the number of molecules striking on unit volume of the walls of the container. P ∝ \(\frac{1}{V}\) …………(2)
From the above two points A and B it is clear that the actual pressure exerted on the wall due to gaseous molecular is less than the ideal pressure.
Actual Pressure (P) = Ideal Pressure (Pi) – Pressure Correction (Pc)
P = Pi – Pc
Pi = P + Pc …………….(3)

Volume correction : At high pressure the molecules are closer and covering/ occupying a considerable minimum area or volume. (Because the space available for the molecule to move is less than the actual volume of the container. Hence Vander waal accounted for this by subtracting volume correction ‘b’ from the observed volume V.
Ideal Volume (Vi) = V – b ………………(6)
We know that if Pi and Vi are pressure and volume of ideal gas then it satisfies PiVi = RT
But from (5) and (6) the ideal pressure and ideal Volumes are substituted.
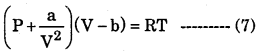
Equation (7) is called Vander waal equation for one mole of gas. This equation for ‘n’ moles of gas is
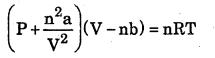
![]()
Question 4.
Interpret PV – P curves based on Vander waals equation.
Answer:
Consider Vander waals eqution for one mole of a gas \(\left(p+\frac{q}{V^{2}}\right)(V-b)=R T\) ……………(1)
Case 1: At low pressure:-
When the pressure is low b = 0
∴ Equation becomes

PV > RT
Explains gradual increase in PV < RT. Hence the curve first descends at lower pressure.
Case 2 ; At high pressure : At high pressure, \(\frac{\mathbf{a}}{\mathbf{V}^{2}}\) = 0 ∴ Equation becomes P(V – b) = RT or PV – Pb = RT PV > RT
Explains gradual increase in PV with simultaneous increase is pressure.
Case 3 : Change in temperature :
At low temperature the value of P and V are very small, hence deviate from ideal behavior.
At high temperature P and V are very large such that \(\frac{\mathbf{a}}{\mathbf{V}^{2}}\) and b are negligible hence
Vander waals Eqn reduces to PV = RT.
∴ At high temperature almost all gases behaves like ideal gas.
Question 5.
Two flasks ‘A’ and <B’ have equal volumes. Flask ‘A’ contains H2 and is maintained at 300 E while ‘B’ contains equal mass of CH4 gas and is maintained at 600 E.
(i) Which flask contains greater number of molecules? How many times more?
(ii) In which flask pressure is greater? How many times more?
(iii) In which flask molecules are moving faster?
(iv) In which flask the number of collisions with walls are greater?
Answer:
(i) Number of moles in flask A = 8 × number of moles in flask B.
Let the equal mass be x. Ratio of number of moles => \(\frac{x}{2}: \frac{x}{16}\) = 8:1
(ii) Pressure α number of moles Pressure α temperature
If temperature had been equal, pressure in ‘A’ would have been 8 times but in ‘A’
temperature is \(\frac{1}{2}\) of that in B
∴Pressure will be 4 times more
![]()
Pressure in flask A = 4 x Pressure in flask B.
(iii) Flask B, because velocity is directly proportional to square root of temperature.
(iv) Flask A, because number of molecules of flask A is more.
![]()
Question 6.
Calculate the pressure exerted by 1.00 mol of CO2 (g) at 298 K that occupies 65.4 ml using Van der waal’s equation.
‘a’ for CO2 is 3.592 L2 bar/mol2, ‘6’ = 0.0427 L mol-1. Compare it with the pressure predicted by ideal gas equation for same conditions of T and P?
Answer:

Question 7.
A gaseous mixture contains 2.2 bar He, 1.1 bar H2 and 4.2 bar N2 . What is mole fraction of N2 ?
Answer:
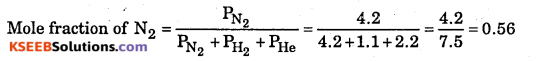
Question 8.
Account for the following:
(a) The size of weather balloon becomes larger and larger as it ascends up into higher altitudes.
(b) Copper is malleable and ductile whiles sulphur is not.
Answer:
(a) At higher altitudes, atmospheric pressure decreases, therefore, air inside the weather balloon exerts pressure and its size becomes larger and larger as it ascends higher and higher.
(b) Copper is metal and has strong metallic bond, that is why it is malleable and ductile. Sulphur is non-metal and has weak intermolecular force of attraction therefore it is brittle.
Question 9.
(a) Explain Boyle’s law with the help of kinetic theory of gases.
(b) An open beaker at 27 °C is heated to 477 °C. What fraction of air would have been expelled out?
Answer:
(a) The kinetic theory of gases assumes that pressure of gas is due to collision of gas molecules with the walls of the container. The more will be frequency of collision, more will be pressure. The reduction in volume (v) of gas increases no. of molecules per unit volume to which pressure is directly proportional. Therefore, the volume of the gas is reduced if pressure is increased or we can say pressure is inversely propotionsl to volume P ∝ \(\frac{1}{V}\)
(b)

Question 10.
(a) What do you mean by ‘Surface Tension’ of a liquid?
(b) Equal volumes of two gases A and B diffuse through a porous pot in 20 and 10 seconds respectively. If the molar mass of A be 80, find the molar mass of B.
Answer:
(a) Surface Tension of a liquid is the force by which surface molecules are attracted towards the bulk.

![]()
Question 11.
(a) Why air is dense at the sea level? Explain.
(b) Calculate the total pressure in a mixture of 4g of O2 and 2g of H2
confined to a total volume of 1L at 0 °C. (R = 0.821 L atm mol-1)
Answer:
(a) Heavier gas will come down and lighter air goes up. Air at sea level is denser due to compression by mass of air above it.

Question 12.
Shown below is a volume vs temperature graph at different pressures P1>P2>P3 an<P4.
(a) Which gas law does this depict?
(b) What does each line of this graph called?
(c) What is the value of temperature at the point where the lines intercept at
temperature axis and what is the specific name given to this hypothetical temperature?
(d) Giving reason arrange the pressures, p1,p2,p3 and p4 in increasing order.
Answer:
(a) Charle’s law.
(b) Isobar.
(c) – 273.15 °C, absolute zero is a lowest hypothetical temperature at which gases are supposed to occupy zero volume.
(d) p1 < p2 < p3 < p4
Reason : For a particular value of temperature : If volume is more it means pressure is less hence p1 is lesser than p2 and so on.
Question 13.
Density of a mixture of gases CO and CO2 is 1.5 g/L at 303 K temperature and 73 cm of Hg. What is the mole percentage of two gases in the mixture?
Answer:
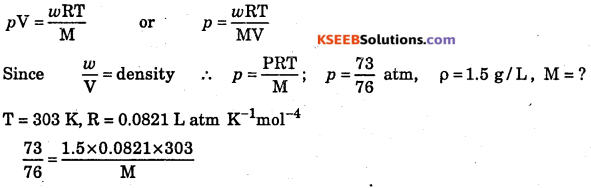
M = 38.85 (Molecular mass of the mixture)
Let total moles = 100
Moles of CO = a and Moles of CO2 = 100 – a
Mass of CO = 28a
Mass of CO2 =(100 – a)44
Total Mass = 28 a + (100 – a)44
Molecular mass of the mixture = \(=\frac{28+(100-a) 44}{100}\) = 38.85(evaluated)
a =32.19
Molecular percentage of CO = 32.19
Mole percentage of CO2 = (100 α) = 100 – 32.19 = 67.81
Question 14.
The van der waal’s equation of state for 1 mole of gas is \(\left(\mathbf{P}+\frac{a}{\mathbf{V}^{2}}\right)(\mathbf{V}-\mathbf{b})=\mathbf{R} \mathbf{T}\)
Arrange the following gases in order of increasing value of ‘a’. The gases are CO2, H2, He and N2. How does the value of V related to the ease of liquifaction?
Answer:
H2 < He < N2 < CO2 is the order of increasing value of ‘a’. Measure of ‘a’ is proportional to the amount of force of intermolecular attraction. CO2 molecule being larger in size, has higher magnitude of van der Waal’s force of attraction and hence highest value of ‘a’.
Also higher is the intermolecular force of attraction, easier it is to liquefy a gas ie., higher the value of ‘a’, higher will be the case of liquefaction.
![]()
Question 15.
In an attempt to record critical temperature of some substances, the value of water has been missed out.
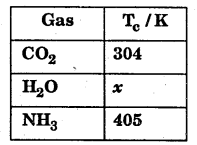
Will the value of x be more or less than (a) CO2 ? (b) NH3 ? Reason out your answers. Also arrange CO2, H2O and NH3 in the order of ease of liquefaction.
Answer:
Value of x will be more than for both CO2 and NH3. This is because in CO2 only weak Van der waals forces exist but in H2O intermolecular H-bonding exist. Also magnitude of H-bonding in H2O is more than in NH3.
H2O has more intermolecular force of attraction therefore it should be easily liquefiable. It is already liquid at room temperature and atmospheric pressure.
Ease of liquefaction CO2 < NH3 < H2O.
Question 16.
An open vessel at the temperature 27 °C is heated until \(\frac { 3 }{ 5 }\) parts of the air in it has been expelled. Assuming that the volume of the vessel remains constant, find the temperature to which the vessel has been heated.
Answer:
For the open vessel, pressure and volume remains contant. If rej moles me present at T1 and n2 moles are present at T2 then
pV = n1RT1 and pV = n2RT2 => n1RT1 = n2RT2
n1T1 = nT2 => \(\frac{n_{1}}{\mathrm{T}_{1}}=\frac{n_{2}}{\mathrm{T}_{2}}\)
Let number of moles of air originally present = n
After heating, number of moles of air expelled = \(\frac { 1 }{ 2 }\) n

Question 17.
In a hospital, an oxygen cylinder of capacity 10 L, oxygen is filled at 200 atmospheric pressure. If a patient breathes in 0.50 ml of oxygen at 1.0 atm with each breath, for how many breaths the cylinder will be sufficient? Assume temperature to be constant.
Answer:
10 L at 200 atm pressure = V2L at 1 atm pressure
P1V1 = p2V2 => 200 × 10 = 1 × V2
V2 = 2000 L
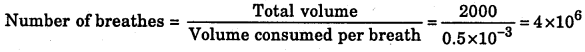
Question 18.
Two flasks of equal volume are connected by a narrow tube of negligible volume and are filled with N2 gas when both the flasks are immersed in boiling water the gas pressure inside the system is 0.5 atm. Calculate the pressure of the system when one of the flasks is immersed in ice water while the other flask in boiling water. ‘
Answer:
Temperature of the gas when flasks are in boiling water = 100 °C = 100 + 273 = 373 K
Pressure = 0.5 atm
Average temperature of the gas when one flask is in ice and other in boiling water. =50°C = 50 + 273 = 323 K

Question 19.
(i) Which of the liquids in each of the following pairs has higher vapour pressure : (a) Alcohol, glycerine ; (b) Petrol kerosene; (c) Mercury, water
(ii) Which one in each of the following pairs JU m ire viscous (a) coconut oil, castor oil ; (b) glycerine, kerosene ; (c) soft drinks, aerated water (soda water)?
(iii) Separate portions of chloroform and water at the same temperature are poured on your hands. The chloroform will feel colder. Account for this in terms of attractive forces.
Answer:
(i) (a) Alcohol (b) Petrol (c) Water
(ii) (a) Castor oil (b) Glycerine (c) Soft drink
(iii) (a) Chloroform molecules have weak van der waal’s forces between them, while water molecules have hydrogen bonding between them. Since van der waal’s forces are weaker chloroform evaporates easily and causes cooling.
Question 20.
Deduce the relation PV = nRT, where R is a constant called universal gas constant.
Answer:
According to Boyle’s law, V ∝ \(\frac { 1 }{ P }\) (at constant T and n)
According to Charle’s law, V ∝ \(\frac { 1 }{ T }\) (at constant P and n)
According to Avogadro’s law, V ∝ (at constant T and P)
Combining the three laws, V ∝ \(\frac { nT }{ P }\) or PV ∝ nRT
Or PV = nRT where R is a constant called universal gas constant.
Question 21.
(i) What is the effect of temperature on (a) density, (b) surface tension, (c) viscosity and (d) vapour pressure of a liquid?
(ii) What is the effect of pressure on (a) volume, (b) boiling point and
(c) viscosity of a liquid?
Answer:
(i) (a) Density decreases (b) Surface tension decreases (c) Viscosity decreases (d) Vapour pressure increases with rise in temperature.
(ii) (a) Volume decreases (b) B. pt increases (c) Viscosity increases with increase in pressure.
Question 22.
An LPG cylinder when full contains 14.2 kg gas and exerts pressure of 2.5 atm. If half of its gas is consumed what will be the pressure of the gas in the cylinder?
Answer:
In a LPG cylinder, the gas is held as a liquid. There is an equilibrium between the LPG (liquid) and its vapour. The equilibrium vapour pressure does not depend upon the quantity of liquid present there as long as liquid ……….. vapour equilibrium is maintained. Therefore, even when half the gas has been used, the pressure excited by ’ the vapour of the gas remains equal to 2.5 atm.
![]()
Question 23.
Why at extremely low pressures, the real gases obey the ideal gas equation?
Answer:
At low pressures, volume V is very large and hence the correction term b (a constant of small value) can be neglected in comparison to very large value of V. Thus the van der waal’s equation for 1 mole of a real gas.

Question 24.
Explain the following observations.
(a) Aerated water bottles are kept under water during summer.
(b) Liquid ammonia bottle is cooled before opening the seal.
(c) The tyre of an automobile is inflated at lesser pressure in summer than in winter.
Answer:
(a) Aerated water contains C02 gas dissolved in aqueous solution under pressure and bottles are well stoppered. As in summer the temperature increases and we know that the solubility of the gases decreases with increase of temperature and as a result more of gas is expected to be generated in the bottle thereby pressure exerted by the gas in the bottle will increase. If the bottles are not kept under water, the gas generated may be large in quantity and hence pressure exerted by the gas may be very high and the bottle may explode. So, to decrease the temperature and hence to avoid explosion of the bottles.
(b) Liquid Ammonia bottle contains the gas under very high pressure. If the bottle is opened as such, then the sudden decrease in pressure will lead to a large increase in the volume of the gas. As a result, the gas will come out the bottle with force. This will lead to the breakage of the bottle. Cooling under tap water will result in the decrease of volume. It reduces the chances of accident.
(c) The pressure of the air is directly proportional to the temperature. During summer
due to high temperature the pressure in the tyre will be high as compared to that in water. The tube may burst under high pressure in summer. Therefore, it is advisable to inflate the tyres to lesser pressure in summer than in winter.
Question 25.
(i) State the law depicting the volume temperature relationship, (ii) Name the temperature at which the volume of the gas becomes equal to zero.
Answer:
(i) The law is known as Charle’s law. Charle’s Law : Pressure remaining constant, the volume of a given mass of a gas increases or decreases by \(\frac { 1 }{ 273 }\) of its volume at 0 °C for every one degree centigrade rise or fall in temperature.
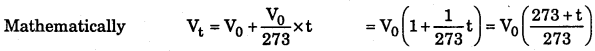
Where Vt = Volume of the gas at t °C and V0 is its volume at 0 °C.
(ii) The temperature at which the volume of a gas becomes equal to zero is called absolute zero.
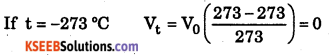
Absolute zero (0 K) = -273 °C
ie., the volume of gas = 0; because, before attaining this temperature, molecular motion of the gas is negligible, ie., they freeze. Gas no longer remains as gas.
Question 26.
Explain the following statements :
(i) Sodium chloride pieces are harder than sodium metal.
(ii) Copper is ductile and malleable but brass is not.
(iii) Latent heat of fusion of solid carbon dioxide is much less than that of silicon dioxide.
(iv) Water has its maximum density near 277 K.
(v) Ice floats on surface of water near the melting point.
Answer:
(i) It has stronger electrostatic forces than metallic bond in sodium.
(ii) Copper is a pure element while brass is an alloy. Pure metal is more malleable.
(iii) SiO2 has covalent bonds while CO2 has only Van der waal’s forces (molecular solid). Hence SiO2 has higher heat of fusion.
(iv) Below 277 K and above 277 K, water expands hence its volume increases, density decreases and is maximum at 277 K
(v) At 0 °C or 273 K, its density is less than that of water hence floats.
Question 27.
What is the concept of Maxwell-Boltzmann distribution of molecular speeds, at a given temperature in a gas sample?
Answer:
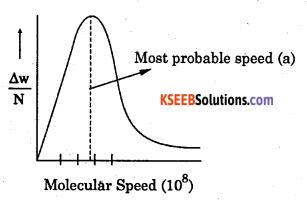
Concept s A gas consists of tiny particles (atom or molecules) separated from one another by large spaces. These particles are constantly moving in all directions. . During their motion, they collide with one another and also with the walls of the container. As a result of collisions, the speed and the direction of the molecules go on changing. Thus, all the molecules present in given sample of a gas do not possess the same speed. The speeds of individual molecules are different and are distributed over a wide range. The speeds of different molecules go on changing. However, the distribution of speed among different molecules remains the same at a particular temperature although the individual speeds of the molecules may change.
The distribution of molecules between different possible speeds was given by Maxwell and Boltzmann. He plotted the fraction of molecules, ie.,\(\frac{\Delta \mathrm{N}}{\mathrm{N}}\) (along y-axis) having different speeds against the speeds of the molecules (along x-axis). The curve so obtained is shown in Fig. below and is known as Maxwell’s distribution curve.
The important features of Maxwell’s distribution curve can be summarized as follows:
- The fraction of molecules with very low or very high speeds is very small.
- The fraction of molecules possessing higher and higher speeds goes on increasing till it reaches the peak and then it starts decreasing.
- The maximum fraction of molecules possesses a speed, corresponding to the peak in the curve. The speed corresponding to the peak in the curve is referred to as most probable speed.
![]()
1st PUC Chemistry States of Matter Numerical Problems and Answers
Question 1.
Calculate the RMS velocity of oxygen at STP.
Answer:
At STP P = 1.013 × 105 Pa
V = 22.4 × l0-3m3
Molecular weight of oxygen = 32 × 10-3 kg
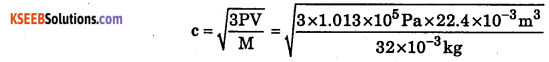
= 461.23 metres per second, c = 461.23 ms-1
Question 2.
Calculate the RMS velocity of a molecule of nitrogen at STP.
Answer:
At STP P = 1.013 × 105 Pa
v = 22.4 × 10-3m3
Molecular weight of nitrogen = 28 × 10-3 kg
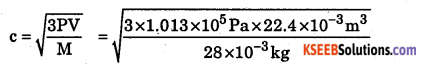
c = 493.07ms-1
Question 3.
Calculate the RMS velocity of methane molecules at 298 K. R = 8.3 14 J K-1mol-1. Molecular weight of methane =16 × 10-3 kg.
Answer:
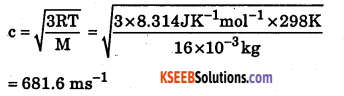
Question 4.
The density of oxygen gas at STP is 1.429 gL-1. Find the RMS velocity.
Answer:
At STP, P = 1.013 × 105Pa; d = 1.429gL-1 in mters it is

Question 5.
At what temperature will the rms velocity of hydrogen be the same as that of nitrogen at 350 K?
Answer:
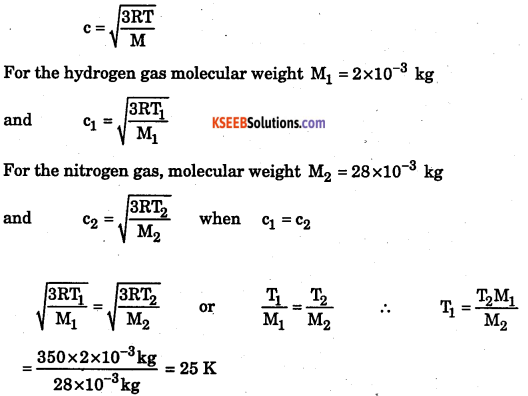
Question 6.
At what temperature will the RMS velocity of oxygen be twice at 200 K?
Answer:
Let c1 be the rms velocity at 200 K (T1)
At temperature T2, c2 = 2c1

Question 7.
Calculate the total kinetic energy of 320 g of sulphur dioxide at 273 K.
Answer:
(KE) n mole = \(\frac { 3 }{ 2 }\) × nRT
T = 273K n = \(\frac { 320g }{ 64g }\) = 5
\(\frac { 3 }{ 2 }\) × 5 × 8.314 × 273 = 17020J
Question 8.
Calculate the total kinetic energy of 2 moles of chlorine at 300 K.
Answer:
(KE)nmoies = \(\frac { 3 }{ 2 }\) × nRT;
n = 2; T = 300 K
= \(\frac { 3 }{ 2 }\) × 2 × 8.314 × 300 =7482.0 J
Question 9.
Calculate the kinetic energy of one mole of helium having RMS velocity K2ms-1.
Answer:
Helium molecule is monoatomic, M = 4g = 4 × 10-3 kg
(KE)mole = \(\frac { 1 }{ 2 }\) Mc2 = \(\frac { 3 }{ 2 }\) x 4 x 10-3 x (102)2 = \(\frac { 1 }{ 2 }\) × 4 × 10 = 20J
Question 10.
Calculate the kinetic energy of one mole of nitrogen at 400 K.
Answer:
(KE)mol =\(\frac { 3 }{ 4 }\) RT=\(\frac { 3 }{ 2 }\) × 8.314 x JK-1mol-1 × 400K = 498.9 J mol-1.
Note: From problems 16 and 19, it can be observed that the kinetic energy of one mole of any two gases, at the same temperature will be the same.
![]()
Question 11.
Calculate the kinetic energy of 300 molecules of CO at 30 °C.
Answer:

Question 12.
Calculate the total kinetic energy of the molecules of nitrogen per cm3 at STP and per m3 at STP.
Answer:
1 mole of a gas occupies 22400 cc at STP
KE of 22,400 cc of a gas at STP = KE of 1 mole of a gas at STP
= \(\frac { 3 }{ 2 }\) x RT = \(\frac { 3 }{ 2 }\) x 8.314 × 273 =3404.58 J
KE of 1 cc of a gas = \(\frac { 3404.58 }{ 22400 }\) = 0.152 J
KE of a m3 of a gas = 0.152 × 106 = 152 × 103 J.
Question 13.
Calculate the RMS speed of a molecule of hydrogen chloride at STP (The molar volume of any gas at STP = 22.4dm3
Answer:
\(\mathrm{c}=\sqrt{\frac{3 \mathrm{PV}}{\mathrm{M}}}\)
where p = 1.01325 × 1015Nm-2
1.01325 × 1015kgm-1s-2
V = 22.4dm<sup<3mol-1 = 0.0224m3mol-1
M = 0.03645kgmol-1
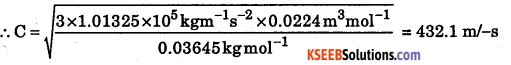
This can be worked out using the relation \(\mathrm{c}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}\)
R = 8.314 J K-1 mol-1
M = 0.03645 kg mol-1

Question 14.
Calculate the Root Mean Square velocity of a nitrogen molecule at 300 K and at a pressure of 2 × 10sNm–2
Answer:

Question 15.
Calcùlate the Root Mean Square velocity of a nitrogen molecule at 300 K and at a pressure of 2 × 105 Nm-2
Answer:
1 mole of nitrogen at STP occupies a volume of 0.0224 m3 and weighs 0.028 kg.

![]()
Question 16.
Through the two ends of a glass tube of length 200 cm, hydrogen chloride gas and ammonia are allowed to enter. At what distance does ammonium chloride first appear?
Answer:
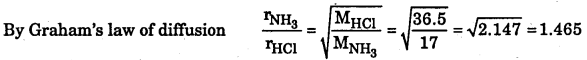
Thus NH3 travel 1.465 times faster than HCl. In other words, NH3 will travel 1.465 cm in the same time in which HCl travels 1 cm.
Length of the tube = 200 cm

Thus, NH4Cl will first appear at a distance of 118.9 cm from NH3 end or 81.1 cm from HCl end.
Question 17.
Calculate the pressure exerted by 110 g of carbon dioxide in a vessel of 2 L capacity at 37 °C. Given that the van der waals constants are a = 3.59 L2atmmol-2 and b = 0.0427 L mol-1. Compare the value with the calculated value if the gas were considered as ideal.
Answer:
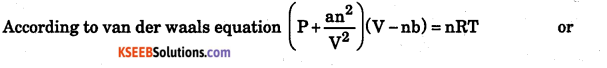

Question 18.
One mole of SOa gas occupies a volume of 350 ml at 27 °C and 50 atm pressure. Calculate the compressibility factor of the gas. Comment on the type of deviation shown by the gas from ideal behavior.
Answer:
Compressibility factor, Z = \(\frac{\mathrm{PV}}{\mathrm{nRT}}\)
Substituting, n = 1 mol, P = 50 atm, V = 350 × 10-3 L = 0.35 L
R = 0.0821 L atm K-1mol-1, T = 27 + 273 = 300 K, we get

For ideal gas, Z = 1. As for th given gas Z < 1, it shows negative deviation ie., it is more compressible than expected from ideal behavior.
Question 19.
The Van der waals constant ‘b’ for oxygen is 0.0318 L mol-1. Calculate the diameter of the oxygen molecule.
Answer:

Question 20.
The boiling point of n – hexane is 68.9 °C. Calculate its approximate critical temperature.
Answer:
According to Goldberg’s rule, for a liquid Tb = \(\frac { 2 }{ 3 }\)Tc
Hence Tc = \(\frac { 2 }{ 3 }\)Tb = \(\frac { 2 }{ 3 }\) (38.9 + 273)K = 512.85 – 273°C
![]()
Question 21.
Assuming CO2 to be Van der waal’s gas, calculate its Boyle temperature. Given a = 3.59 L2atm mol-2 and b = 0.0427 Lmol-1.
Answer:
Boyle temperature in terms of Van der waal’s constants is TB = \(\frac{\mathrm{a}}{\mathrm{Rb}}\)

Question 22.
A cylinder of 20.0 L capacity contains 160 g of oxygen gas at 25 °C. What mass of oxygen must be released to reduce the pressure of the cylinder at 1.2 atm?
Answer:
Number of moles of oxygen gas present initially in the cylinder is
= \(\frac{160 \mathrm{g}}{32 \mathrm{g} \mathrm{mol}^{-1}}\) = 5 moles
(Molar mass of 02 = 32 g mol-1)
To calculate the number of moles now present, we have P = 1.2 atm, T = 298 K, V = 20.0 L
Applying the relation, FV = nRT, we have,
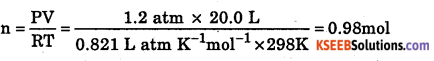
∴ Number of moles of 02 required to be released = 5 – 0.98 = 4.02 mol
Or Mass of to be released = 4.02 × 32 g = 128.64 g.
Question 23.
50 litre of dry N2 is passed through 36 g H2O at 27 °C. After the passage of the gas, the mass of water was reduced to 34.80 g. Calculate the aqueous tension of water at 27 °C.
Answer:
Water carried away by N2 gas = 36 – 34.80 = 1.20 g
As this water is carried away by 50 L of N2 gas, this means that volume occupied by water vapours = 50 L. Thus, now we have n = \(\frac { 1.20 }{ 18 }\) = 0.0667mol, V = 50 L, T = 300
K, P = ?
Applying the gas equation, PV = nRT

= 0.03286 × 760 mm = 24.97 mm.
Question 24.
A 5 L vessel contains 1.4 g of nitrogen. When heated to 1800 K, 30% of molecules are dissociated into atoms. Calculate the pressure of the gas at 1800 K.
Answer:

∴ Total number of moles = 0.035 + 0.030 = 0.065
i.e., n = 0.065 mol, V = 5L, T – 1800 K, P = ?
Applying PV = nRT, we get
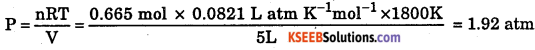
Question 25.
The volume expansion of a gas under constant pressure is 0.037. Calculate its volume at – 100 °C if its volume at 100 °C is 685 cm3.
Answer:
Volume expansion of a gas means increase or decrease in volume per degree rise or fall in temperature of its volume at 0 °C.
Vt = V0 + 0.0037 × V0 × t = V0(l + 0.0037t)
At 100 °C, V1oo°C = v0 (1 + 0.0037 × 100) = 685cm3 (Given)
Or V0= \(\frac{685}{1.37}\) = 500cm3
At -100°C, V-1oo°C=500[1 + 0.0037 × (-100)] = 315cm3
![]()