Students can Download 1st PUC Physics Model Question Paper 5 for Practice, Karnataka 1st PUC Physics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Model Question Paper 1 with Answers
Time: 3.15 Hours
Max Marks: 70
General Instructions:
- All parts are compulsory.
- Draw relevant figure / diagram wherever necessary.
- Numerical problems should be solved with relevant formulae.
Part – A
I. Answer the following questions. ( 10 × 1 = 10 )
Question 1.
Write the S I unit of momentum.
Answer:
kg ms-1
Question 2.
Is scalar multiplied by a vector, a vector or a scalar?
Answer:
It is a vector
Question 3.
Write an expression for position vector of centre mass of system of two particles lie on x – axis
Answer:
X = \(\frac{m_{1} x_{1}+m_{2} x_{2}}{m_{1}+m_{2}}\)
![]()
Question 4.
Mention the expression for work done by a force in vector form.
Answer:
W = \(\vec{F} \cdot \vec{S}\)
Question 5.
State Hook’s law.
Answer:
With in elastic limit, stress is directly proportional to strain.
Question 6.
Among rubber and steel which one has more elasticity?
Answer:
Steel.
Question 7.
What is ideal gas?
Answer:
A gas which obeys both Boyle’s law and Charle’s law is called ideal gas.
Question 8.
Define angle of contact.
Answer:
It is an angle between the tangent drawn to the surface of liquid at the point of contact with the surface of contact with in the liquid.
Question 9.
State the first law of thermodynamics.
Answer:
The law stats that heat energy given to the system is equal to sum of the increase in internal energy and work done by the system.
![]()
Question 10.
Mention any one applications of beats.
Answer:
- Beats are used to tune the musical instruments.
- They are used to detect the poisonous gases in mines, or any use.
Part – B
II. Answer any FIVE of the following questions. ( 5 × 2 = 10 )
Question 11.
Mention any two basic forces in nature.
Question 12.
Mention two uses of dimensional analysis
Question 13.
Distinguish between distance (path length) and displacement.
Answer:
| Distance or path length | Displacement |
| 1. It is the length of the path along which the body moved. | 1. It is the shortest distance between initial final positions. |
| 2. It a scalar. | 2. It is a vector. |
| 3. It cannot be negative. | 3. It can be negative, positive or zero. |
Question 14.
What is centripetal acceleration? Give the expression for it.
Answer:
The acceleration of a body towards the centre of a circular path along which the body moves.
a = ν2 / r = r2ω
![]()
Question 15.
Mention any two methods of reducing friction.
Question 16.
Determine the volume contraction of the solid copper cube, 10 cm on its edge, when subjected to hydraulic pressure of 7.0 × 106 Pa. (Given bulk modulus of copper = 140 × 109 Nm-2).
Answer:
\(B=\frac{P}{\frac{\Delta V}{V}}=\frac{P V}{\Delta V} \Rightarrow \Delta V=\frac{P V}{B}=\frac{7 \times 10^{6} \times 10^{3} \times 10^{-6}}{140 \times 10^{9}}\)
= 0.05 × 10-3
ΔV = 5 × 10-5 m3
Question 17.
What is specific heat capacity of a substance? Write the relation between specific heat capacities of gases.
Answer:
It is the quantity of heat required to raise temperature of one kg of substance through one degree Celsius.
Cp – Cv = R
Question 18.
On an average the human heart is found to beat 75 times in minute. Calculate its frequency.
Answer:
f = number of oscillations /time
f = \(\frac{75}{60}\) = 1.25 Hz.
Part – C
III. Answer any FIVE of the following questions. ( 5 × 3 = 15 )
Question 19.
State and explain Law of triangle of vectors. When will be the resultant of two given vectors is maximum?
Question 20:
State Newton’s second law of motion and hence derive F = ma.
![]()
Question 21.
Prove work- energy theorem for a constant force.
Question 22.
Derive an expressions orbital speed of the earth’s satellite.
Question 23.
State and explain Bernoulies theorem.
Question 24.
Write any three properties of heat radiation.
Question 25.
State the law of equipartition of energy. Write an expression for the energy associated with diatomic molecule.
Answer:
Energy associated with distance molecule is V = 5 \(\left(\frac{1}{2} R T\right)\)
Question 26.
Discuss the modes of vibrations in closed path.
Part-D
IV. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 27.
Derive x = v0t + \(\frac{1}{2}\) at2 by graphical method.
Question 28.
State and prove the law of conservation of linear momentum in case of collision of two bodies.
Question 29.
Derive the relation between torque and angular momentum of a particle.
V. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 30.
State and explain Kepler’s laws of planetary motion.
![]()
Question 31.
Write a note on kelvin scale of temperature.
Answer:
From Charles law V = V0 (1 + αt) … (1)
If t = -273°C, then(1) ⇒ V = V0 \(\left(1-\frac{273}{273}\right)\), V = 0
Volume of gas becomes zero at -273°C theoretically which is shown in the above fig. But practically all known gases become liquids before attaining this temperature (-273°C). From Charles law this is the lowest possible temperature.
Lord Kelvin made a scale by taking -273°C as lowest temperature. It is called absolute scale of temperature. The lowest temperature is called absolute zero (0K = -273°C). The temperature on the Kelvin scale is called absolute temperate. The width of each degree on the Kelvin scale is equal to the width of each degree on Celsius scale. The relation between Celsius scale temperature (t) & Kelvin scale temperature (T) is given by
T = (t + 273) K
Question 32.
Derive an expression for period of simple pendulum.
VI. Answer any THREE of the following questions. ( 3 × 5 = 15 )
Question 33.
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 ms-1 can go without hitting the ceiling of the hall?
Answer:
h = \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
25 = \(\frac{(40)^{2} \sin ^{2} \theta}{2 \times 9 \cdot 8}\)
∴ θ = sin-1 (0.5534) = 33.60°
Horizontal range R = \(\frac{u^{2} \sin 2 \theta}{g}\) = 150.33 m
Question 34.
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?
Answer:
P0 = \(\frac{\text { Work done }}{\text { Time }}=\frac{m g h}{t}\)
= \(\frac{30 \times 10^{3} \times 9 \cdot 8 \times 40}{900}\) = 13.067 × 103 W
For input power Pi, efficiency η is given by the relation:
n = \(\frac{P_{0}}{P_{i}}\) = 30%
Pi = \(\frac{13 \cdot 067}{30}\) × 100 × 103
=0.436 × 105 W = 43.6 kw
Question 35.
A 5 kg wheel is given an acceleration of 10 rad/sec2 by an applied torque of 2 N-m. Calculate its (a) moment of inertia and (b) radius of gyration.
Answer:
I = \(\frac{\tau}{\alpha}=\frac{2}{10}\)
I = 0.2 kgm2
And I = MK2
K = 0.2m
![]()
Question 36.
A steam engine delivers 5.4 × 108 J of work per minute and serves 3.6 × 109 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute.
Answer:
η = \(\frac{w}{q_{1}}\) = 5.4 × 108 / 3.6 × 109 = 15%
Q2 = Q1 – W
= 36 × 108 – 5.4 × 108 = 30.6 × 108 J
Question 37.
A train standing at the outer signal of railway station blows a whistle of frequency 400Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10m/s. (b) recedes from the platform with a speed of 10m/s? (ii) What is the speed of the sound in each case, the speed of sound in still can be taken as 340m/s.
Answer:
f’ = \(\frac{f v}{\left(v-v_{s}\right)}\)
=400 (340-0) / 340-10) = 412 Hz
f” = \(\frac{f v}{\left(v+v_{s}\right)}\)
f” = 400(340) / (340+10) = 389 Hz
Karnataka 1st PUC Physics Model Question Paper 2 with Answers
Time: 3.15 Hours
Max Marks: 70
General Instructions:
- All parts are compulsory.
- Draw relevant figure / diagram wherever necessary.
- Numerical problems should be solved with relevant formulae.
Part – A
I. Answer the following. ( 10 × 1 = 10 )
Question 1.
Mention the SI unit of luminous intensity.
Answer:
Candela.
Question 2.
Define null vector.
Answer:
A vector having zero magnitude.
Question 3.
What is potential energy?
Answer:
Energy possessed by a body by virtue of its position or configuration.
Question 4.
Write the expression for moment of inertia of a solid sphere of radius R about its diameter.
Answer:
I = \(\frac{2}{5}\) MR2
![]()
Question 5.
Write the distance of the geostationary satellite from the center of the earth.
Answer:
42200 km
Question 6.
State Hooke’s law.
Answer:
Within the elastic limit, the stress in a body is directly proportional to strain.
Question 7.
What is the principle behind the uplift of an aeroplane?
Answer:
Bernoulli’s principle.
Question 8.
Give an example for Greenhouse gas.
Answer:
Carbon dioxide, nitrous oxide methane, chlorofloro carbon etc.
Question 9.
What is the physical significance of Zeroth law of thermodynamics?
Answer:
Temperature
![]()
Question 10.
Which quantity remains unchanged in isochoric process?
Answer:
Volume
Part – B
II. Answer any FIVE of the following questions. ( 5 × 2 = 10 )
Question 11.
Name any two fundamental forces in nature.
Question 12.
Write two applications of dimensional analysis.
Answer:
- Checking the dimensional consistency of equations
- Deducing relation among the physical quantities
Question 13.
Distinguish between ‘path length’ and ‘displacement’.
Answer:
| Path length | Displacement |
| 1. It is a scalar | 1. It is a vector |
| 2. Is always positive | 2. Positive or negative or zero |
Question 14.
Write the equation for the trajectory of a projectile motion. What is the nature of its trajectory?
Answer:
y = x tanθ – \(\frac{g x^{2}}{v_{0}^{2} \cos ^{2} \theta_{0}}\) and trajectory is parabola.
![]()
Question 15.
State the two laws of friction.
Answer:
- Limiting friction is independent of area of surface of contact of two bodies
- Magnitude of limiting friction is directly proportional to normal reaction.
Question 16.
Write the equation for escape velocity and explain the terms used in the equation.
Answer:
Escape velocity : ve = \(\sqrt{2 R g}\) or v0 = \(\sqrt{\frac{2 G M}{R}}\)
R is radius of the earth, G is gravitational constant and M is mass of the earth.
Question 17.
Where is the velocity of the body maximum and minimum in case of simple harmonic motion?
Answer:
- Mean position or equilibrium position
- Extreme position
Question 18.
What harmonics are present in a) an open pipe b) a closed pipe?
Answer:
(a) All harmonics
(b) Odd harmonics
Part – C
III. Answer any FIVE of the following questions. ( 5 × 3 = 15 )
Question 19.
Define centripetal acceleration? Write the expression for it and explain the terms.
Answer:
Definition:
\(a_{c}=\frac{v^{2}}{r}\)
Where v is velocity and r is radius of the circle.
![]()
Question 20.
Deduce f = ma, using Newton’s second law of motion.
Question 21.
What is meant by collision? Distinguish between elastic and inelastic collision.
Question 22.
Draw stress-strain curve. Show yield point and fracture point.
Question 23.
Mention three applications of capillarity.
Answer:
- Rise of oil through wick of the lamp
- Rise of water in the plant through xylem in plants
- Absorption of ink by blotting paper/chalk piece
Question 24.
Derive σv = \(\frac{1}{T}\) for ideal gas.
Question 25.
Draw schematic diagram of the refrigerator. Define its coefficient of performance.
![]()
Question 26.
Give the Newton’s formula for the speed of sound in air and hence explain Laplace’s correction.
Answer:
According to Newton v = \(\sqrt{\frac{p}{\rho}}\)
Part – D
IV. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 27.
What is v-t graph? Derive the equation x = v0t + \(\frac{1}{2}\) at2 using v – t graph.
Question 28.
State and prove the law of conservation of linear momentum from Newton’s third law of motion.
Question 29.
Define torque and hence derive \(\frac{d \vec{l}}{d t}=\vec{\tau}\)
V. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 30.
Derive the expression tor the variation of the acceleration due to gravity with altitude.
Question 31.
Explain Carnot cycle with P-V diagram.
Question 32.
Derive the expression for the time period of the simple pendulum.
VI. Answer any THREE of the following questions. ( 3 × 5 = 15 )
Question 33.
A ball is thrown with the velocity of a 39.2 m/s at an angle of 30° with the horizontal. Calculate the maximum height, time of flight and horizontal range of the projectile.
Answer:
Maximum height, Hm = \(\frac{v_{0}^{2} \sin ^{2} \theta}{2 g}\) = 19.6 m
time of flight, tf = \(\frac{2 v_{0} \sin \theta}{g}\) = 4s
Horizontal range, R= \(\frac{v_{0}^{2} \sin 2 \theta}{g}\) = 135.79 m
![]()
Question 34.
A bullet of mass 50 gram moving with a velocity of 400 m/s strikes a wall and goes out from the other side with a velocity of 100 m/s. Calculate the work done in passing through the wall.
Answer:
Work done W = KE2 – KE1
KE1 = \(\frac{1}{2} m_{1} v_{1}^{2}\) =4000 J
KE2 = \(\frac{1}{2} m v_{2}^{2}\) = 250 J
Arriving at final answer
W = KE2 – KE1 = 4000 – 250 = 3750 J
Question 35.
Three pieces of iron of uniform thickness and mass m , m and 2m respectively are placed at the three corners of the triangle having co-ordinate (2.5, 1.5),(3.5, 1.5) and (3, 3) respectively. Find the center of mass of the system.
Answer:
x = \(\frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}}{m_{1}+m_{2}+m_{3}}\) = 3m
y = \(\frac{m_{1} y_{1}+m_{2} y_{2}+m_{3} y_{3}}{m_{1}+m_{2}+m_{3}}\) = 2.25 m
Writing the co-ordinates of the centre of mass
Question 36.
How much it is required to convert 10 gram of ice at – 5° into steam at 100°C. Given specific heat of ice 2.1 J g-10 C-1. Latent heat of steam = 2268 J g-1 and latent hear of fusion of ice is 336 J/g. Specific heat of water = 4.2 J g-10 C-1.
Answer:
Q1 = mSi ΔT = 10 × 2.1 × 5 = 105 J
Q2 = mLf = 10 × 336 = 3360 J
Q3 =mSw ΔT = 10 × 4.2 × 100 = 4200 J
Q4 =mLv =10 × 2268 = 22680 J
Q = Q1 + Q2 + Q3 + Q4
= 105 + 3360 + 4200 + 22680 = 30345 J
![]()
Question 37.
The apparent frequency of a note when listener moves towards a stationary source with velocity 40 m/s is 200 Hz. When he moves away from the same source with same speed the apparent frequency of note is 160 Hz. Calculate velocity of sound in air.
Answer:
When the listener move towards source
\(r^{\prime}=\left(\frac{v+v_{0}}{v}\right) v\) …(1)
When the listener move away from the source \(v^{\prime \prime}=\left(\frac{v-v_{0}}{v}\right) v\) …(2)
(1) ÷ (2),
\(\frac{v^{\prime}}{v^{\prime \prime}}=\left(\frac{v+v_{0}}{v-v_{0}}\right)\)
Solving and finding v =360 ms-1
Karnataka 1st PUC Physics Model Question Paper 3 with Answers
Time: 3.15 Hours
Max Marks: 70
General Instructions:
- All parts are compulsory.
- Draw relevant figure / diagram wherever necessary.
- Numerical problems should be solved with relevant formulae.
Part – A
I. Answer the following ( 10 × 1 = 10 )
Question 1.
Write the dimensional formula for linear momentum.
Answer:
M1L1T-1
Question 2.
What is unit vector?
Answer:
It is the vector having unit magnitude.
Question 3.
Define work done by the force.
Answer:
Work is said to be done when force is applied on the body and the body displaces in the direction of applied force. w= \(\vec{F} \cdot \vec{S}\)
![]()
Question 4.
Define radius of gyration.
Answer:
It is the distance between the point at which the entire mass of the body is concentrated from the axis of rotation.
Question 5.
What is the weight of a body at the centre of the earth?
Answer:
zero
Question 6.
Name the SI unit of stress.
Answer:
Nm-2
Question 7.
What is streamline flow?
Answer:
It is the motion in which velocity of all the particles of fluid is same at a given point.
Question 8.
Mention the degrees of freedom for a triatomic gas molecule.
Answer:
6
Question 9.
Write Newton’s formula for speed of sound in air.
Answer:
\(V=\sqrt{\frac{p}{\rho}}\)
![]()
Question 10.
Define amplitude of a wave.
Answer:
It is the maximum displacement of oscillating particle on either side of its mean position.
Part – B
II. Answer any FIVE of the following questions. ( 5 × 2 = 10 )
Question 11.
Name any two fundamental forces in nature.
Question 12.
Mention any uses of dimensional analysis.
Answer:
- To check the correctness of an equation.
- To derive the relation between various physical quantities.
Question 13.
State triangle law of vector addition.
Question 14.
Mention any two methods of reducing friction.
Question 15.
Define average velocity and instantaneous velocity.
Question 16.
State and explain first law of thermodynamics.
Question 17.
Write the relation between g and G and explain the terms.
Answer:
g = \(\frac{G M}{R^{2}}\)
Explanation of terms
![]()
Question 18.
Mention an expression for the period of oscillation of a spring and explain the terms.
Answer:
T = \(2 \pi \sqrt{\frac{m}{k}}\)
Explanation of terms
Part – C
III. Answer any FIVE of the following questions. ( 5 × 3 = 15 )
Question 19.
Obtain an expression for time of flight of a projectile.
Question 20.
Using Newton’s second law of motion, arrive at F = ma,
Question 21.
Derive an expression for kinetic energy.
Question 22.
Mention the three types of moduli of elasticity.
Answer:
- Young’s Modulus (Y)
- Bulk Modulus (B)
- Rigidity modulus (R)
Question 23.
State and explain Bernoulli’s principle.
![]()
Question 24.
Define (a) Specific heat of gas at constant volume (b) Specific heat of gas at constant pressure (c) Latent heat of fusion.
Question 25.
Write any three postulates of kinetic theory of gasses.
Question 26.
Give any three differences between progressive wave and a stationary wave.
Answer:
| Progressive wave | Stationary wave |
| 1. The wave travel forward with a velocity called wave velocity. | 1. The wave do not travel in any direction. |
| 2. There is transfer of energy along the direction of propagation of wave. | 2. There is no transfer of energy across any section of the medium. |
| 3. No particle of the medium is permanently at rest. | 3. Particles at nodes are always at rest. |
Part – D
IV. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 27.
What is uniform circular motion? Derive an expression for centripetal acceleration.
Question 28.
State and explain a) Parallel axis theorem and b) perpendicular axes theorem.
![]()
Question 29.
Derive an expression for maximum speed of a car moving on banked circular road.
Answer:
Figure
N cos θ = Fs sin θ + mg
N = \(\frac{m g}{\cos \theta-\mu_{s} \sin \theta}\)
v = \(\frac{r g\left(\sin \theta+\mu_{s} \cos \theta\right)}{\cos \theta-\mu_{s} \sin \theta}\)
v = \(\sqrt{\frac{r g\left(\tan \theta+\mu_{s}\right)}{\left(1-\mu_{s} \tan \theta\right)}}\)
V. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 30.
Define Orbital speed of a satellite. Obtain an expression for the orbital speed of satellite.
Question 31.
State and explain the Newton’s law of cooling.
Question 32.
What is SHM? Write its characteristics and give its graphical representation.
VI. Answer any THREE of the following questions. ( 3 × 5 = 15 )
Question 33.
A stone is dropped from top of a tower 100 m height. At the same instant another stone is thrown vertically upward from the base of the tower with the velocity of 25 m/s. When and where will the two stones meet?
Given g = 10 m/s2.
Answer:
For Stone A, u = 0, S = x and a = + g = 10 m/s2
Formula s = ut + \(\frac{1}{2}\) at2
Arriving at x = 5t2 —(l)
For stone B s = 100 – x, a = – g and u = 25 m/s
Arriving at 100 – x = 25t – 5t2 …(2)
Obtaining t = 4 second
Obtaining x = 80 m
![]()
Question 34.
A bullet of mass 0.015 kg strikes a metal plate of thickness 10 cm with a velocity of 400 m/s and emerge from it with a velocity of 260 m/s. Find the average resistance offered by the plate to the motion of bullet.
Answer:
Formula work done = \(\frac{1}{2} m u^{2}-\frac{1}{2} m v^{2}\)
Substitution and obtaining w = 693 J
W=FS
F = 6930 N
Question 35.
A fly wheel of mass 12.5 kg and diameter 0.36 m rotating at 90 rpm has its speed increased to 720 rpm in 8s. Find the torque applied to flywheel.
Answer:
ω1 = 2πf1 = 3π rad/sec
ω2 = 2πf2 = 24 π rad/sec
α = ω2 – ω1 / t = 8.243 rad/s2
τ = 1α = (Mr2 / 2) α
τ = 1.669 Nm
Question 36.
A Carnot engine has an efficiency of 0.3, when the temperature of the sink is 350K. Find the change in temperature of the source when the efficiency becomes 0.5.
Answer:
η1 = 1 – \(\frac{T_{2}}{T_{1}}\)
Solving for T = 500 K
η2 = 1 – \(\frac{T_{2}}{T_{1}^{2}}\)
Solving for T11= 700K
Change in temperature = 200 K
![]()
Question 37.
A train is moving at speed of 72 kmph towards a station, is sounding a whistle of frequency 600 Hz. What are the apparent frequencies of the whistle as heard by a man on the plot form when the train (a) approaches him (b) recedes from him? (speed of sound in air = 340 m/s)
Answer:
Formula
a) f′ = \(\left(\frac{V}{V-V_{s}}\right)\) f
obtaining f = 637.5 Hz
b) f′ = \(\left(\frac{V}{V+V_{s}}\right)\) f
Obtaining f = 566.7 Hz
Karnataka 1st PUC Physics Model Question Paper 4 with Answers
Time: 3.15 Hours
Max Marks: 70
General Instructions:
- All parts are compulsory.
- Draw relevant figure / diagram wherever necessary.
- Numerical problems should be solved with relevant formulae.
Part – A
I. Answer the following ( 10 × 1 = 10 )
Question 1.
How many meters make one parsec?
Answer:
3.08 × 1016 m.
Question 2.
What is unit vector?
Answer:
A vector whose magnitude is equal to one.
Question 3.
When does the work done by a force is zero?
Answer:
If the force acts at angle of 90° or if the displacement is zero.
Question 4.
Define torque.
Answer:
The rotating effect of the applied force is called torque.
![]()
Question 5.
Mention the value of escape speed of an earth satellite?
Answer:
11.2 km/s
Question 6.
State Pascal’s law.
Answer:
It states that if change in pressure is produced in any part of an enclosed fluid (liquid or gas), the same is transmitted equally to all points of the fluid in all directions.
Question 7.
Give Principle of calorimetry.
Answer:
If there is no loss of heat energy by radiation, heat lost by hot body is equal to heat gained by cold body.
Question 8.
What is equation of state for adiabatic process?
Answer:
PVϒ = constant
Question 9.
Name a factor on which internal energy of the gas depends.
Answer:
Temperature/pressure.
![]()
Question 10.
What happens to the time period of a simple pendulum when it is taken from equator to the pole?
Answer:
2 seconds.
Part – B
II. Answer any FIVE of the following questions. ( 5 × 2 = 10 )
Question 11.
Mention any two basic forces in nature.
Answer:
Gravitational force, Electrostatic force and nuclear force.
Question 12.
The resistance R = \(\frac{v}{I}\) where V = (100 ± 5) volt and I = (10 ± 0.2)A, Find the percentage error in R.
Answer:
The percentage error in V is 5% and that in current is 2% therefore error in R is 5%+ 2% = 7%
Question 13.
Distinguish between distance and displacement.
Answer:
| Distance | Displacement |
| 1. It is the actual path length between the initial and final positions of the body during motion. | 1. It is the shortest distance between the initial and final positions of the body during motion. |
| 2. It is a scalar quantity. | 2. It is a vector quantity. |
| 3. It is never zero or negative, but is always positive. | 3. It may be zero or positive or negative. |
Question 14.
Write the expression for range of the projectile? For what angle of projection it is maximum?
Answer:
R = \(\frac{u^{2} \sin 2 \theta}{g}\) if θ = 45°.
![]()
Question 15.
Mention two methods of reducing friction.
Question 16.
Give two general conditions of equilibrium of a rigid body.
Question 17.
Define Gravitational potential energy: Give expression for it.
Answer:
Energy possessed by the body by virtue of its position or configuration.
P.E = mgh.
Question 18.
What is Doppler effect? Mention one of its applications.
Answer:
Apparent change in the frequency of source of sound due to relative motion between source and the observer.
It is used in SONAR, over speeding of the vehicles RADAR etc.
Part – C
III. Answer any FIVE of the following questions. ( 5 × 3 = 15 )
Question 19.
Derive the expression for centripetal acceleration.
Question 20.
State Newton’s first law of motion? Hence define force and inertia.
Question 21.
Prove work-energy theorem for a constant force.
![]()
Question 22.
Compare equations of linear and rotational motion.
Question 23.
Derivation of pressure at a point inside a liquid.
Question 24.
State Stefan’s law and Draw the intensity distribution graph of black body radiation.
Answer:
It states that the total amount of heat energy radiated per second per unit area of a perfect black body is directly proportional to the fourth power of the absolute temperature of the surface of the body.
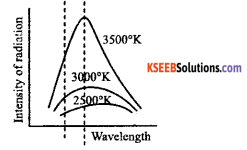
Question 25.
Mention three postulates of Kinetic theory of gases.
Question 26.
Explain Laplace’s correction to Newton’s formula for the Speed of a sound wave.
Part – D
IV. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 27.
Derive x = v0t + \(\frac{1}{2}\) at2 by graphical method.
![]()
Question 28.
Derive the expression for maximum safe speed of a vehicle on a banked road in circular motion.
Question 29.
State and explain the parallel axis and perpendicular axis theorem.
V. Answer any TWO of the following questions. ( 2 × 5 = 10 )
Question 30.
State and explain Hooke’s law. Draw Stress – strain curve with labeling the parts.
Question 31.
Graphically represent the variation of coefficient of volume expansion of copper as a function of temperature. Derive α V = \(\frac{1}{T}\) for an ideal gas.
Question 32.
Derive the expression for time period of a simple pendulum.
VI. Answer any THREE of the following questions.( 3 × 5 = 15 )
Question 33.
A particle starts from origin at t = 0 with a velocity 5î ms-1 and moves in x-y plane under the action of a force which produces a constant acceleration of (4î + 2\(\hat{j}\)) ms-2.
(a) What is the y-coordinate of the particle at an instant when its x-coordinate is 84 m?
(b) What is the speed of the particle at this time?
Answer:
\(\vec{r}=\vec{v}_{0}+\frac{1}{2} \vec{a} t^{2}\)
X (t) = 5t + 2t2
Y(t) = 1.0 t2
t = 5.26 s
Y(t) = 27.7 m
V = 28.08 m/s
![]()
Question 34.
A pump on the ground floor of a building can pump up water to All a tank of volume 40m3 in 20 minutes if the tank is 30m above the ground and the efficiency of the pump is 60%. How much electric power is consumed by the pump? Given density of water = 1000 kg/m3 and acceleration due to gravity = 9.8m/s2.
Answer:
\(P_{0}=\frac{W}{t}=\frac{m g h}{t}=\frac{\rho V m g h}{t}\)
Substitution
P0 =9.8 × 10+3 W
P0 = 9.8 kW / 0.6 = 16.33 kW
Question 35.
The planet Mars take 1.88 years to complete on revolution around the sun. The mean distance of the earth from the Sun is 1.5 x 108 km. Calculate that of planet Mars?
Answer:
\(\frac{T^{2}}{a^{3}}\) = constant
\(\frac{T_{2}^{2}}{T_{1}^{2}}=\frac{a_{2}^{3}}{a_{1}^{3}}\)
Substitution
a2 = 22.8 × 1010 m
Question 36.
A steam engine delivers 7.5 × 108 J of work per minute and services 3.6 × 109 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute? Also And the ratio of temperature of sink to the source.
Answer:
η = \(\frac{p_{0}}{p_{1}}\)
η = 0.21
P0 = Pi = 47.5 MW
η = 1 – \(\frac{T_{1}}{T_{2}}\)
\(\frac{T_{1}}{T_{2}}\) = 0.79
![]()
Question 37.
A particle executes SHM along the x-axis, its displacement varies with the time according to the equation: x(t) = 5.4 cos (6πt + π/4), where x(t) in metre and t is in second. Determine the amplitude, frequency, period and initial phase of the motion.
Answer:
Determine the amplitude, frequency, period and initial phase of the motion.
x(t) = 5.4 cos (6πt + \(\frac{\pi}{4}\))
A = 5.4 m
n = 3 Hz
T = 0.333 s
Initial phase = Φ = \(\frac{\pi}{4}\)