1st PUC Statistics Question Bank Chapter 9 Elements of Probability Theory

You can Download Chapter 9 Elements of Probability Theory Questions and Answers, Notes, 1st PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.

Karnataka 1st PUC Statistics Question Bank Chapter 9 Elements of Probability Theory

1st PUC Elements of Probability Theory Question and Answers

Question 1.
What do you mean by ‘probability’?
Answer:
Measurement of chances is called ‘Probability.’

Question 2.
Define Random experiment
Answer:
An experiment in which the outcomes of that experiment cannot be predictable, is called Random experiment.Eg., tossing a coin, throwing a die.

Question 3.
Define Trial and Event
Answer:
Conducting an experiment is called Trial, and getting an outcome is an Event.
Eg. Tossing a coin is a trial and getting outcome Head Or Tail are Events.

Question 4.
What is sample space?
Answer:
The set of all possible outcomes of a random experiment. Denoted by S
S = {H,T}, S = {1,2,3,4,5,6}

Question 5.
Define Exhaustive events
Answer:
Total number of all possible outcomes of a random experiment is called Exhaustive events.denoted by ‘n’. in the above examples, n=2 & n=6.

Question 6.
Define Favourable events
Answer:
The number of outcomes which entail as an outcome, or number of outcomes which favours the happening of an event, denoted by ‘m’
Eg., in the above example to get H, m = 1, & to get ‘Even’ no. S={2,4,6}, m=3.

Question 7.
What are Mutually Exclusive events?
Answer:
Two or more events are said to be mutually exclusive, if no two events can occur at a time in the same trial. Eg, When a coin is tossed getting Head in a trial is mutually exclusive of getting Tail in the same trial.

Question 8.
What are Equally likely events?
Answer:
Outcomes of a random experiment are called equally likely if they have equal chance of occurrence.Eg. When a die is thrown, all outcomes to get 1,2,.. .6 are having equal chance to get as an outcome.

Question 9.
What are Independent events?
Answer:
The outcomes of a random experiment are said to be independent if the happening of an Event in the trial is independent of getting the same (or other) Event in the subsequent trials.Eg., Getting Head in the first Toss is independent of getting Head in the second toss of a coin.

Question 10.
What are Complementary events
Answer:
Let S be the sample space, A be an event, then A‘ is called complementary event of A is it contains elements of S, but it does’t contain any elements of event
Eg., S = {1,2,3,4,5,6} if A = {1,2}, then A = {3,4,5,6}

Question 11.
Give the Classical/Priori/Mathematical definition of probability.
Answer:
Let a random experiment have n possible outcomes which are equally likely, mutually exclusive and exhaustive. Let m of these outcomes be favourable to an event A. Then, probability of A

Question 12.
Write down Posterior/Statistical definition of Probability
Answer:
Let a random experiment be repeated n times essentially under identical conditions. Let m of these repetitions results in the occurrence of an event A. Then, the probability of event A is the limiting value of the ratio m/n as n increases indefinitely.

Here, it is assumed that a unique limit exists.

Question 13.
Write down the Axiomatic definition of Probability.
Answer:
Let A and B be the events of a sample space S. Let P(A) and P(B) are the real numbers (probabilities) assigned to these events. Then, P(A) is the probability of A if, the following axioms are satisfied.
Axiom (i) : P(A) ≥ 0 (non-negativity condition)
Axiom (ii) : P(S) = 1. ‘S’ being the sure event.
Axiom(iii): For any two disjoint events A and B,P(A + B) = P(A) + P(B)

Question 14.
Prove that 0 ≤ P[A] ≤ 1
Answer:
statement: 0 ≤ P(A) ≤ 1. That is, P(A) is the value between 0 and 1
(The limits of probability are 0 and 1).
Proof: Here, by definition of probability of an event A is P(A) = \(\frac { m }{ n }\)
The least and highest possible values of m are zero and n.
That is, 0 ≤ m ≤ n dividing by n
\(\frac{\mathrm{o}}{\mathrm{n}} \leq \frac{\mathrm{m}}{\mathrm{n}} \leq \frac{\mathrm{n}}{\mathrm{n}}\)
i.e., 0 ≤ P(A) ≤ 1

Question 15.
Show P[A]+P[A¹]=1
Answer:
P(A) + P(A²) = 1. That is, the sum of probabilities of complementary events is 1.
Proof: We knowthat, Out of ‘n’ outcomes, if ‘m’ outcomes are favourableto event A, then the remaining (n-m) outcomes are favourable to event A¹.
By definition P(A) = \(\frac { m }{ n }\) and P(A²) = \(\frac { n-m }{ n }\)
\(\therefore \mathrm{P}(\mathrm{A})+\mathrm{P}\left(\mathrm{A}^{2}\right)=\frac{\mathrm{m}}{\mathrm{n}}+\frac{\mathrm{n}-\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{m}+\mathrm{n}-\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{n}}{\mathrm{n}}=1\)

Question 16.
StatetheAdditiontheoremforanytwoevents.
Answer:
Statement: Let A and B be two events with respective probabilities P(A) and P(B). Then, the probability of occurrence of at least one of these two events is
P (A ∪ B) = P(A) + P(B) – P(A ∩ B) or
P(A+B) = P(A) + P(B) – P(AB)

Question 17.
State the Addition theorem for any two mutually exclusive events.
Answer:
Let A and B be two mutually exclusive events with respective probabilities P (A) and P(B). Then, the probability of occurrence of at least one of these two events is
P(A ∪ B) = P(A) + P(B) or
P(A+B) = P(A) + P(B)

Question 18.
State the Multiplication theorem for any two Independent events.
Answer:
Statement: Let A and B be two independent events with respective probabilities P(A) and P(B). Then, the probability of simultaneous occurrence of Aand B is
P(A ∩ B)= P(A) × P(B).

Question 19.
Define conditional probability.
Answer:
The probability of occurrence of one event under the condition that another event has already occurred is known as conditional probability.
The probability that B will occur under the condition that Alias already occurred is denoted by

Similarly, The probability that A will occur under the condition that B has already occurred is denoted by P(A/B).

Question 20.
If P[A]=l/4, what is P[A’]?
Answer:
P(A) + P(A²) = 1 or P(A²) = 1- P(A);
P(A²) = 1-1/4 ; P(A²) = 3/4

Question 21.
Find the probability of getting head when a coin is tossed.
Answer:
when a coin is tossed the sample space S ={Head, Tail};
n(s) = 2; n(H)=l;

Question 22.
P(H) = \(\frac { 1 }{ 2 }\). If P[A]=2/5 and P[B]=l/5. Find P[A∪B], when A and B are Mutually exclusive events
Answer:
we know that, P(A ∪B) = P(A) + P(B);
P(A ∪B) = 2/5 + 1/5
∴ P(A ∪ B) = 3/5

Question 23.
P[A]=3/4, P[B]=l/2 and P[A∪B]=l/4. Find P[A)”B] and P[A/B]
Answer:
we know that; P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
1/4 = 3/4 + 1/2 – P(A ∩ B)
P(A ∩ B) = 3/4 + 1/2 – 1/4
∴ P(A∩B) = 1/2 = 0.5

Question 24.

Answer:
we know that, P (A ∪ B) =P(A)+P(B)-P(A∩B)
= 1/3 + 2/3 – 3/4
=0.33 + 0.67 – 0.75
P(A∪B) = 0.25

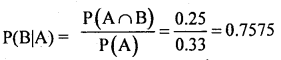
Question 25.
IfP[ABl=l/3 and P[B]=2/3, find P[A/B]
Answer:
we know that P(B/A) – p(A) =

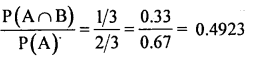
Question 26.
IfP[A ∩ B]=l/2, and P[B]=2/3, find P[A/B]
Answer:
We know that P(A/B) =

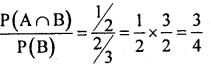
Question 27.
If P[B]=3/5 and P[A/B]=l/3 find P[B ∩ A]
Answer:

Question 28.
IfP[A]=l/2, P[B]=l/3 and P(A ∩ B)=l/4, find P[B/A] and P[AUB].
Answer:
we know that; P(A∪B) = P(A) + P(B) – P(A ∩ B)
P(A∪B)= 1/2+ 1/3 – 1/4 = 0.5833

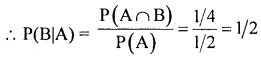
Question 29.
IfP[A∪B]=l/3, P[A ∩ B]=l/12 and P[A]=l/6, find P[B].
Answer:
P(A∪B) = P(A) + P(B)- P(A∩B)
1/3 = 1/6 + P(B) – 1/12;  1/3 – 1/6 + 1/12 = P(B)
∴ P(B) = 0.25

Question 30.
IfP[A]=0.5, P[B]=0.1 and P[A ∪B]=0.7, find P[A/B].
Answer:

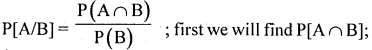
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
0. 7 =0.5 + 0.1 -P(A ∩B);  ∴ P(A ∩B) = 0.7 – 0.5 – 0.1 =0.1

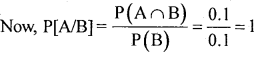
Question 31.
If the sample space S={1,2,3,4,5,6} and A={3,4}, find P[A}
Answer:
Here n= 6 and m = 2 ; ∴ P(A) = m/n = 2/6 =0.33

Question 32.
If P[A]=l/8, P[B]=l/6 and P[A∪B]=1/10, find P[A ∩ B].
Answer:
P(A∪B) = P(A) + P(B) – P(A∩B)
1/10= 1/8+ l/16 – P(A∩B)
P(A∩B)= 1/8 + 1/16 – 1/10 = 0.0875

Question 33.
If P[B/A]=2/5 and P[A]=5/6, find P(B ∩ A)
Answer:

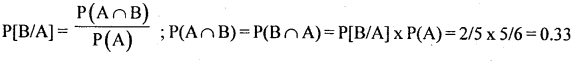
Question 34.
A bag contains 4 white, 2 pink and 3 Black balls. A ball is drawn at random, What is the probability that it is
1. a white
2. a pink
3. either pink or black ball.
Answer:
Here total bal Is 4(W) + 3 (B) + 2(P) = 9 and n = 9
1. m Favorable ways to draw a white ball = 4
P(drawing a white ball) = P(B) = \(\frac { m }{ n }\) = \(\frac { 4 }{ 9 }\)

2. m = pink balls = 2
P(pink) = \(\frac { 2 }{ 9 }\)

3. m = either pink or black ball = 2 + 3 = 5
∴ P(pink or black) = \(\frac { 5 }{ 9 }\)

Question 35.
A card is drawn from a wll su filed pack of placing cards. Find the probability that the card draw is
(a) a King
(b) a club
(c) a Red
(d) a King or Queen
(e) an Ace or Spade.
Answer:
n=Total cards=52
(a) m = No. of Kings = 4
∴ P (drawing an king card) = \(\frac { m }{ n }\)= \(\frac { 4 }{ 52 }\)

(b) m = clubs = 13
P(club) = \(\frac { 13 }{ 52 }\)

(c) m = Red cards = 13(Hearts) + 13(Diamonds) = 26
P(Red card) = \(\frac { 26 }{ 52 }\)

(d) m : King or Queen = 4 + 4 = 8
P(K or Q) = \(\frac { 8 }{ 52 }\)

(e) m = An ace or a club card = 4+13-1 = 16
(Since there is a card, which is a Ace and a Club)
P(Ace or Club) = \(\frac { 16 }{ 52 }\)

Question 36.
Adie is thrown. Find the probability that the face of a die results in
1. multiple of 2
2. multiple of 3
3. an odd number.
Answer:
S= {1,1, 3,4,5,6}: n = 6
1. m = multiple 2 : (2, 4, 6) = 3
P(multiple of 2) = \(\frac{m}{n}=\frac{3}{6}=\frac{1}{2}\)

2. m = multiple of 3 : (3, 6) = 2
P(multiple of 3) = \(\frac{2}{6}=\frac{1}{3}\)

3. m = odd number : (1, 3, 5) = 3
P(odd no.) = \(\frac{3}{6}=\frac{1}{2}\)

Question 37.
Two coins are tossed, find the probabiliti getting
1. both coins heads
2. exactly one head
3. no heads
4. atleast one head.
Answer:
S = {HH, HT, TH, TT} : n = 22 = 4
1. m = both heads : (HH) =1
P(2H) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{1}{4}\)

2. m = exactly one H: (HT, TH) = 2
P(one heads) = \(\frac{2}{4}=\frac{1}{2}\)

3. m : no heads : (TT) =1
P(no head) = p(2T) = \(\frac { 1 }{ 4 }\)

4. m = atleast one H : (HT, TH, HH) = 3
P(atleast one H) = \(\frac { 3 }{ 4 }\)

Question 38.
Three coins are tossed, find the probability of getting
1. Exactly one Head
2. Exactly 2H
3. No ehads/only tails
4. Atleast one Tail.
Answer:
S = {HHH, HHT, HTT, TTT, TTH, THH, THT, HTH} : n = 23 = 8
1. m = Getting exactly one Head : (HTT, TTH, THT) = 3 .
P(One H) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{3}{8}\)

2. m = Exactly 2 H : (HHT, THH, HTH) = 3
P(2H) = \(\frac { 3 }{ 8 }\)

3. m = no heads/ Tails only : (TTT) =1
P(No heads/Tails only) = \(\frac{m}{n}=\frac{1}{8}\)

4. m = Atleast one Tail: Except (HHH) = 7
P(Atleast one Tail) = \(\frac { 7 }{ 8 }\) OR
P(A) = p(getting atleast one T) = 1 – P (Not getting No Tail) .
= l- P(A’)=l – \(\frac { 1 }{ 8 }\) = \(\frac { 7 }{ 8 }\)

Question 39.
Two dice are rolled once. Find the probability of getting
1. both with number 5
2. first die with no.
3. sum on both the dice is 7
4. sum is 10 or more
5. both with same no.
Answer:
n = 6² = 36
1. m = both with no. 5 = (5, 5) = 1
P(both 5) = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{1}{36}\)

2. m = first dice with no. 1 : (1, 1) (1, 2) (1, 3) ……………………. (1, 6) = 6
P(First die with no. 1) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)

3. m = sum is 7 : (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1) = 6
P(sum is 7) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)

4. m = sum is 10 or more : sum (10) or (11) or (12)
(4, 6), (5, 5), (6, 4) + (6, 5), (5, 6) + (6, 6) = 6
P(sum is 10 or more) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)

5. m = Both with same number: (1, 1) (2, 2) (3, 3)
P(both dice with same no.) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)

Question 40.
Two coins are tossed, find the probabiliti getting
1. both coins heads
2. exactly one head
3. no heads
4. atleast one head.
Answer:
S = {HH, HT, TH, TT} : n = 2² = 4
1. m = 2 white marbles = ³C₂ = 3

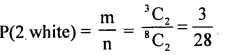
2. m = 2 Red marbles = ⁵C₂ = 10

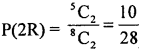
3. m = 2 marbles of same colour: (2W) OR (2R)
= ³C₂ OR ⁵C₂ = 3 + 10 = 13 ways

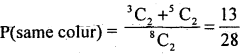
4. m =2 marbles of different colour = 1W and 1R
= ³C₁ × ⁵C₁ = 3 × 5 = 15 ways.

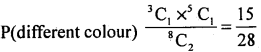
OR P(A) = p(same colour) = 1 – P(A’) = 1 – P (different colour)
∴ P(different colour) = 1 – P(same colour) = \(1-\frac{13}{28}=\frac{15}{28}\)

Question 41.
Two cards are drawn from a peck of 52 playing cards. Find the probability that they are of
1. Kings
2. Clubs
3. Red cards
4. a king and a Ace
5. a Heart and a spade.
Answer:
n = Two cards can bedrawn from 52 cards = ⁵²C₂
n = 1326 ways
1. m = 2 kings from 4 kings can be draw = ⁴C₂ = 6 ways

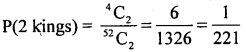
2. m = 2 clubs can be drawn from 13 = ¹³C₂ = 78

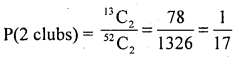
3. m = 2 Red cards can be drawn from 26 = ²⁶C₂ = 325
(i.e., out of 13 diamonds and 13 hearts)

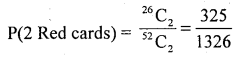
4. m = a king and an Ace can be drawn = ⁴C₁ × ⁴C₁ = 4 × 4 = 16

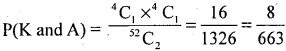
5. m = a Hearts and a spade can be drawn from 13 hearts and 13 spades
= ¹³C₁ × ¹³C₁ = 13 × 13 = 169

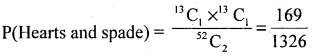
Question 42.
A book rack at home has 4 Novels, 5 magezines and 3 Cockery books. Two books are chosen at raondom. Find the rpboability that the selected books are
1. of the same type
2. of different type
3. only Novels
4. one is a Novel and the ohter is a cokcery.
Answer:
n – (4N + 5m + 3C) = ¹²C₂ =66 :
1. m = 2 books of same type can be drawn
= 2 N or 5 m or 3C = ⁴C₂ + ⁵C₂ + ³C₂
∴ m = 6+ 10 + 3 = 19

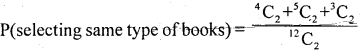
Let P(A) = \(\frac { 19 }{ 16 }\)

2. Let P(A’) = p(selecting different type of books)
P(A’)= 1 – P(A) = 1 – \(\frac { 19 }{ 16 }\) = \(\frac { 47 }{ 66 }\)

3. m = selecting z novels = ⁴C₂

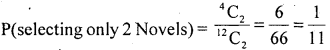
4. m = selecting one Novel other cockery
= ⁴C₁ × ³C₁ =4 × 3 = 12

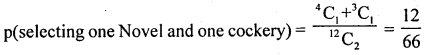
Question 43.
The chance of winning a cricket match by India against Australia is 5/7. Find the probability that India loses against Australia.
Answer:
Let P(A) = p(Indian wins against Australia) = \(\frac { 5 }{ 7 }\)
Then P(A’) = p(India loses agaisnt Australia)
P(A’) = 1 – P(A)
P(A’) = l – \(\frac { 5 }{ 7 }\) = \(\frac { 2 }{ 7 }\)

Question 44.
In a city out of 1200 New born babies in that month, 580 were girls. Find the probability that a new born baby is a girl.
Answer:
Here n = 1200 Total births, m = 580 No. of girls born
P(New born baby is a girl) = \(\frac { m }{ n }\) = \(\frac { 580 }{ 1200 }\) = 0.4833

Question 45.
State and prove addition theorem of propability of two not mutually exclusive events.
Answer:
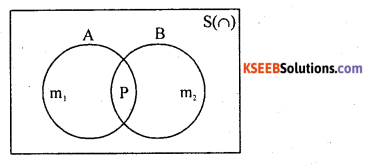
Statement: Let Aand B be any two events (subsets of sample sapce S) with respective probabilite is P(A) and P(B). Then, the probability of occurrence of atleast one of these events is:
P(A ∪B) = P(A) + P(B) – P(A∩B)
Here the event (AnB) is the simultaneous occurrence of A and B.
Proof: A random experiment results ‘n’ exhaustive out comes, of which’m₁ ‘ outcomes are favorable to event A ‘m₂‘ outcomes are favorable to event B and ‘p’ outcomes are common to both A and B.
Consider the venn diagram
‘

The event of occarrence of atleast one of A or B is (A∪B) has (m₁ + m₂ – P) favorable outcomes

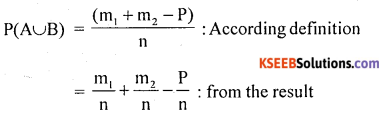
P(A∪B) = P(A) + P(B) – P(A∩B), Hence the proof.

Question 46.
State and prove addition theorem of probability of two mutually exclusive events.
Answer:
Statement: Let A and B be two mutually exclusive events (subsets of sample space S) with respective prababilities P(A) and P(B). Then, the probability of occurrence of atleast one of these events is
P(A∪B) = P(A) + P(B)
Proof: A random experiment results ‘n’ exhaustive outcomes, of which’m’ outcomes are favourable to event A and ‘m₂‘ outcome of are favorable to event B.
Consider the venn diagram.


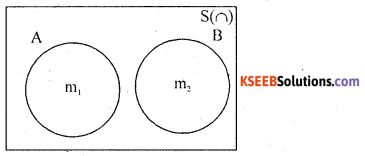
The event of occurrence of atleast oen of A or B is (A∪B) has (m₁ + m₂) favorable out comes.

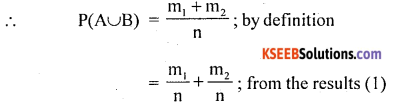
P(A∪B) = P(A) + P(B). Hence the proof.

Question 47.
State and prove multiplication theorem of probability for any two dependent events.
Answer:
Statement: If A and B be any two events in evently in a random experiment. then the probability of occurrence of events A and B is,
P(A∩B) = P(A). P(B/A)
Where the events P(B/A) is the conditional probability of occurrence of event B, known that the event Alias already occurrence.
Proof: Suppose, a random experiment results ‘n’ outcomes, of are favorable events A and B and ‘P’ outcomes are favorable to both the events A and B.

Suppose, event A has occurred, which has’m,’ favorable outcomes to A.
If event ‘B’ occurred, it has out’m’ outcomes, ‘P’ outcomes are favorable to B
∴ Probability of happening of an event ‘B’ known that A has already happened is:

Then, the probability of occurrence of events A and B together is :

P(A∩B) = P(A) × P(B/A) from the results (1) & (2)
Hence the proof.
Note: The conditional probabilities can also be extend to prove : P(B∩A) = P(B). P(A/B)

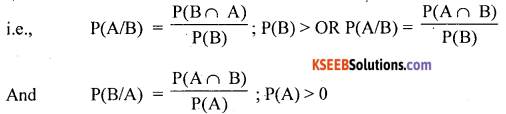
Question 48.
State and prove the multiplication theorem of probabilities for two independent events:
Answer:
Statement: Let A and B be any two independent events with respective probabilities P(A) and P(B). Then, the probability of occurrence of events A and B is P(A∩B) = P(A). P(B)
Proof: Suppose, a random experiment, results ‘n’ outcomes, of which’m’, outcomes are favorable
k to events A and another random experiment results n₂ outcomes of which m₂ outcomes are favorable to event B.

The occurrence of the events A and B together m₁ and m₂ i.e., m₁ × m₂ favorable events out of n₁, and n₂ i.e., n₁ × n₂ outcomes.
∴ Probability of ocurrence of events A and Btogther is.

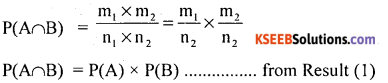
Hence the proof.

Question 49.
A card are drawn from a pack of playing cards. Find the probability that the card drawn is
1. King or a Red
2. Heart or a Red.
Answer:
n = A card can be drawn from 52 cards in 52 ways.
1. Let A = drawing a King = 4
B = drawing a Red card = 26
Here (A∪B) = King and a Red card = 1
P(A∪B) = P(A) + P(B) – P(A∪B) =\(\frac{4}{52}+\frac{26}{52}-\frac{1}{52}=\frac{29}{52}\)

2. Let A – Card drawn is a Heart = 13
B – Card drawn is a Red = 26
and (A∩B) – Heart and Red cards =13
P(A∪B) = P(A) + P(B) – P(A∩B) = \(\frac{13}{52}+\frac{26}{52}-\frac{13}{52}=\frac{26}{52}\)

Question 50.
A Die is trolled once. Find the probability of getting a face with a multiple 2 or multiple of 3.
Answer:
S = {1,2, 3,4, 5,6} ; n = 6
Let A= Multiple of 2 : (2, 4, 6) = 3
B-Multiple of 3 : (3,6) = 3 and (A∩B) common in A and B : (6)= 1
∴ P(A∩B) = P(A) + P(B). P(A∩B) = \(\frac{3}{6}+\frac{3}{6}-\frac{1}{6}=\frac{5}{6}\)

Question 51.
Probability of hitting a target is \(\frac { 1 }{ 3 }\) and that of B is \(\frac { 1 }{ 4 }\). If both attempt to hit the target, what is the probability that
1. both hit
2. the raged is hit.
Answer:
Let P(A) – P(Hittign target by (A) = \(\frac { 1 }{ 3 }\)
P(B) – P(Hitting targed by B) = \(\frac { 1 }{ 4 }\)

1. Since Hitting tanget by A and B are independent
∴ P(A∩B) = P(Both hit) = P(A) x P(B) = \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{12}\)

2. P(the target is hit) = P(Atleast one hit)
= P(A∩B) = P(A) + P(B) – P(A∩B) =\(\frac{1}{3}+\frac{1}{4}-\frac{1}{12}=\frac{6}{12}=\frac{1}{2}=0.5\)

Question 52.
Probability that a student A can solve a problem is \(\frac { 3 }{ 5 }\) and that of B can solve is \(\frac { 5 }{ 7 }\) Find
the probability that
1. both solve
2. atleast one solve
3. None solve the problem.
Answer:
Let P(A) = \(\frac { 3 }{ 5 }\) , P(B) = \(\frac { 5 }{ 7 }\)
1. P(Both solve) = P(A∩B) = P(A). P(B). Since A and B are independent.
\(=\frac{3}{5} \times \frac{5}{7}=\frac{3}{7}\)

2. P(atleast one solve the problem) = P(A∪B) = P(A) + P(B) – P(A∩B)
\(=\frac{3}{5}+\frac{5}{7}-\frac{3}{7}=\frac{31}{35}\)

3. P(None solve the problem)

Question 53.
A can hit a target 2 times with 5 shots. B can hit it 3 times with 4 shots and can hit it 5 times with 8 shots. If they fire at a volley, what is the probability that atleast oen of them hits it?
Answer:
Let P(A) = (A can hit a target)= \(\frac { 2 }{ 5 }\)
Similarly P(B) = \(\frac { 3 }{ 4 }\), P(C) = \(\frac { 5 }{ 8 }\)
P(atleast one of them hit) = P(A∪B∪C) = 1 – P(None hit the target) = 1 – P(A’∪B’∪C’)
Here P(A’) = 1 – P(A) = 1 – \(\frac { 2 }{ 5 }\) = \(\frac { 3 }{ 5 }\), p(B’) = \(\frac { 1 }{ 4 }\), P(c’) = \(\frac { 3 }{ 8 }\)

∴ p(atleast one of them hit) = 1- P(A’). P(B’) P(c’)
\(=1-\left(\frac{3}{5} \times \frac{1}{4} \times \frac{3}{8}\right)=1-\frac{9}{160}=\frac{151}{160}=0.944\)

Question 54.
In a class of 20 girls and 40 boys, half of the girls and half of the boys use cell phones. Find the probability that a student chosen at random is
1. a girl or using cell phone,
2. a boy or a girl
3. a boy or has a cellphone)
Answer:
Let A: Student is a boy = 40,
B : Student is a girl = 20
C : Boy using cell phones = 20,
D: Girls using cell phones =10,
E: Students using cell phone = 30.
1. P(Chosen student is a girl or using cell phone)
= P(B∪E) = P(B) + P(E) – P(A∩E) = \(\frac{20}{60}+\frac{30}{60}-\frac{10}{60}=\frac{40}{60}=\frac{2}{3}=0.67\)

2. P(a boy or a girl) = P(A∪B) = P(A) + P(B)= \(\frac{40}{60}+\frac{20}{60}=\frac{60}{60}=1\)

3. P(a boy or has a cell phone)
P(A∪E) – P(A) + P(E) – P(A∩E) = \(\frac{40}{60}+\frac{30}{60}-\frac{20}{60}=\frac{50}{60}=0.833\)

Question 55.
A machine has two parts A and B and it fails to work either of the parts tails. The probability of part a fails is 0.25 and the probability of part B fails 0.12. Find the probability that the machine fails.
Answer:
Let P(A) : P(part A fails) = 0.25 and P(B): P(part B fails) = 0.12
P (machine fails) =P(partSfails or B fails) = P(A∪B) = P(A) + P(B) – P(A∩B)
= P(A) + P(B) – P(A).P(B)
Since parts A and B are independent
P(A∪B) = 0.25 + 0.12-0.25 × 0.12 = 0.37 – 0.03 = 0.34

Question 56.
An corn contains 9 red balls and 6 yellow balls. If Deeput chooses 2 balls one after the other with replacement. Find the probaiblity that
1. both are red
2. one of each colour.
Answer:
Let A: First ball drawn is red, B : Second ball drawn is red – C: The ball drawn is yellow. Since A and B are independent events
1. P(Drawing 2 red balls one after the other with replacement) = P(A∩B) = P(A). P(B); by multiplication theorem.
\(=\frac{9}{15} \times \frac{9}{15}=\frac{9}{25}=0.36\)

2. P (drawing one of each colour ball)
= P(A∩C) or P(C∩A) = \(\frac{9}{15} \times \frac{6}{15}=\frac{6}{25}=0.24\)

Question 57.
A bowl contains 4 Red and 3 blue marbles. Another bowl contians 3 Red and 5 blue marbles. One of the bowl is randomly chosen and a marble is drawn, what is the probability that it is a blue marble?
Answer:
Let A: First bowl is selected, B : Second bowl is selected, C : Marble drawn is blue.
Here P(A) = P(B) = \(\frac { 1 }{ 2 }\)
P(drawing a blue marble) = P(First bowl is selected and 9 blue marble is drawn from it) Or P(Second bowl is selected and a blue marble is drawn from it)
= P(A∩C) ∩P(B∩C) = P(A). P(C/A) + P(B). P(C/B)
\(=\frac{1}{2} \cdot \frac{3}{7}+\frac{1}{2} \cdot \frac{5}{8}=\frac{3}{14}+\frac{5}{16}=0.527\)

Question 58.
A box has 4 blue and 3 green balls. Another box has 3 blue and 5 green balls A ball is selected from each boxes, find the probability both balls drawn are green.
Answer:
Let A: drawing a green ball from I box
B : drawing a green ball from II box
Since drawing balls from each box sare independent.
∴ P(drawing green balls from both boxes)
= P(A∩B) = P(A).P(B)=\(=\frac{3}{4} \times \frac{5}{8}=\frac{15}{40}=0.375\)

Question 59.
What is the probability that there will be 53 Sundays in a random 4 selected
1. Non-leap year and
2. Leap year.
Answer:
1. ANon-leap year has 365 days, with 52 weeks has 364 days. The remaining one day may be
: Mon, Tue, Wed, Thu, Fri, Sat and San = 7

∴ Probability of 53 Sundays in a non-leap year = \(\frac { 1 }{ 7 }\)

2. A Leap year has 366 days with 52 weeks, has 364 day. The remaining = days may be. (Mon, Tue), (The, Wed), (Wed, Thu), (Thu, Fri), (Fri, Sat), (Sat, Sun) and (Sun, Mon) =
7 possible combination of days.
∴ Probability 53 Sundays in a leep year = \(\frac { 2 }{ 7 }\) ;
i. e., may be of (Sat, Sun), (Sun, Mon)

Question 60.
A study shows that a person randomly chosen will go out to a mall with probability 0.74, and the probability that a person will go to get some chats is 0.45 during a weekend. And the probability that the person will get chats given that he will go to a mall.
Answer:
Let A: Person gets chats, B: Person goes out to a mall.
P(a person gets chats given that he goes to a mall)

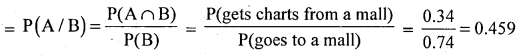
Question 61.
An urn contains 8 black balls and 4 white balls. Two balls are taken from the urn without replacement. Compute the probability that both balls are white.
Answer:
Let A: First balls’s white, B: Second ball is white
P(drawing 2 white balls one after the other without replacements) = P(A∩B) = P(A). P(B/A)
\(=\frac{4}{12} \cdot \frac{3}{11}=\frac{1}{11}=0.0909\)

Question 62
In a bag, there are 8 blue balls and 6 red, 2 balls are picked up one after two other without replacement. So, what is the probability of picking red ball in 2nd attempt knowing that a blue balls has already been picked.
Answer:
A: I ball drawn l’s blue B: II ball drawn is red.
P(A∩B) =P(A).P(B/A) = \(\frac{8}{14} \times \frac{6}{13}\)
Here first ball l’s not replaced.
∴ P(A/B) = \(\frac { 6 }{ 13 }\) is the required