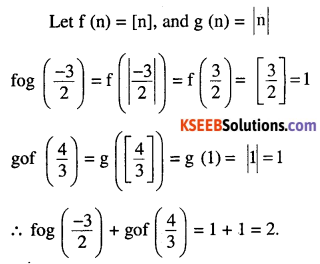Students can Download Maths Chapter 1 Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 1 Relations and Functions Miscellaneous Exercise
Question 1.
Let f : R → R be defined as f (x) = 10x + 7. Find the function g : R → R such that
gof = fog = IR.
Answer:
Since gof = fog = IR ,
(gof) (x) = (fog) (x) = x ∀ x ∈ R
g (f (x)) = f (g (x)) = x
g (10x + 7) = x and

![]()
Question 2.
Let f : W → W be defined as f(n) = – 1, if n is odd and f(n) = n – 1, if n is even. Show that
f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Answer:
Let m, n ∈ W and m and n be 2 distinct elements.
Case I:
When both m and n are even
f(m) = m + 1 f (n) = n + 1
m ≠ n ⇒ m + 1 ≠ n + 1
⇒ f (m) ≠ f (n)
Case II:
When both m and n are odd
f (m) = m – 1 f(n) = n – 1
m ≠ n ⇒ m -1 ≠ n – 1
⇒ f (m) ≠ f (n)
Case III:
When m is odd and n is even
f(m) = m – 1 f (n) = n + 1
f(m) ≠ f (n)
so, in all cases m ≠ n ⇒ f (m) ≠ f (n)
Hence, f is a one-one function.
If n ∈ W is any element
f (n – 1) = n if n is odd (∵ n – liseven)
f(n + 1) = n if n is even (∵ n + 1 is odd)
so, every element of W is the f – image of some element in W.
Hence f is onto
Thus, f is both one-one and onto.
i.e. f is one-one correspondence. Consequently,
f is invertible.
f (n – 1) = n if n is odd
f (n + 1) = n if n is even
n – 1 = f-1 (n) if n is odd
n + 1 = f-1 (n) if n is even
\(\begin{aligned}&\text { i.e. } f^{-1}(n)=\left\{\begin{array}{ll}{n-1} & {\text { if } \quad n \text { is odd }} \\{n+1} & {\text { if } \quad n \text { is even }}\end{array}\right.\\&\text { thus } f^{-1}=f\end{aligned}\)
Question 3.
If f : R → R is defined by f(x) = x2 – 3x +2, find f (f(x)).
Answer:
f (x) = x2 – 3x + 2
∴ f (f (x)) = f (y) where
y = x2 – 3x + 2
= y2 – 3y + 2
= (x2 – 3x + 2)2 – 3 (x2 – 3x + 2) + 2
= x4 + 9x2 + 4 – 6x3 + 4x2 – 12x – 3x2 + 9x – 6 + 2
= x4 – 6x3 + 10x2 – 3x.
![]()
Question 4.
Show that the function f : R → {x ∈ R : – 1 < x < 1} defined by
\(\mathbf{f}(\mathbf{x})=\frac{\mathbf{x}}{\mathbf{1}+|\mathbf{x}|}, \mathbf{x} \in \mathbf{R}\) is one one and onto function.
Answer:


hence f is one-one
similarly we can prove that f is one-one.
When x1 < 0 and x2> 0 and x, < 0 and x2 > 0
To prove f is onto

Question 5.
Show that the function f : R → R given by f (x) = x3 is injective.
Answer:
Let x1 ≠ x2 be any 2 reals
∴ x1 – x2 ≠ 0.
Also,

Question 6.
Give examples of two functions f : N → Z and g : Z → Z such that g : Z → Z is injective but £ is not injective. (Hint: Consider f(x) = x and g (x) = |x|).
Answer:
As g (x) = g (-x) = |x| for all x ∈ Z ,
∴ g is not one-one
i.e. y is not injective
As f : N → Z and g : Z → Z gof : N → Z
let x1, x2, ∈ N such that gof (x1) = gof (x2)
⇒ g (x1) = g (x2)
⇒ | x1 | = | x2 | ⇒ x1 = X2
(both x1 ,x2 >0)
Hence g o f is injective.
![]()
Question 7.
Give examples of two functions f : N → N and g : N → N such that gof is onto but f is not onto. (Hint: Consider f (x) = x + 1 and
\(g(x)=\left\{\begin{array}{r}{x-1 \text { if } x>1} \\{1 \text { if } x=1}\end{array}\right.\)
Answer:
f(x) = x+ lxl + 1 ≥ 1 + 1 ∀ x ∈ N
(∵ v ≥ 1 x ∈ N)
⇒ f(x) ≥ 2 ∀ x ∈ N . Rf ^ N as 1 t Rf
Hence f is not onto
gof : → ∼ → N such that
gof (x) = g (f (x)) = g (x + 1)
= (x+1) -1 [ ∵ ∀ x ∈ N,x+ 1 > 1]
⇒ gof (x) = x V x ∈ N
∴ Range of gof = N as gof is the identity f Hence gof is onto.
Question 8.
Given a non empty set X, consider P(X) which is the set of all subsets of X. Define the relation R in P(X) as follows: For subsets A, B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify your answer.
Answer:
Since A C A ∀ A ∈ P (X)
R is reflexive.
Also, for A, B, C ∈ P(X),A R B & B R C
⇒ A C B and B C C
⇒ A ⊂ C ⇒ A R C
∴ R is transitive.
R is not symmetric as A C B ⇒ B C A
so ARB ⇒ BRA
Hence R is not an equivalence relation.
Question 9.
Given a non-empty set X, consider the binary operation * : P(X) * P(X) → P(X) given by
A * B = A ∩ B ∀ A, B in P(X), where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation *.
Answer:
Let E ∈ P (X) be an identity elements, then
A * E = E * A = A ∀ A ∈ P(X)
⇒ A ∩ E = E ∩ A = A ∀ A ∈ P(X)
⇒ X ∩ E = X as X ∈ P (X)
⇒ X C E
Also E C X as E ∈ P (X)
∴ E = X
Thus, X is the identity element.
Let A ∈ P(X) be invertible, then there exists
B ∈ P(X) such that A * B = B*A = X, the identity element.
⇒ A ∩ B = B ∩ A = X
X C A & X C B
Also A, B, ⊂ X as A, B ∈ P (X)
A = X = B
X is the only invertible element and – X1 = B = X.
![]()
Question 10.
Find the number of all onto functions from the set {1, 2, 3,…, n} to itself.
Answer:
Let A = {1, 2, 3,……… n}
f : A → A is an onto function, then range of f
⇒ f is one-one f is one and onto the number of onto function is nPn = n!
Question 11.
Let S = {a, b, c} and T = {1, 2, 3}. Find F1 of the following functions F from S to T, if it exists.
(i) F = {(a, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2),(i, 1), (c, 1)}
Answer:
(i) Range of {1, 2, 3} = T
⇒ F is onto Also F is onto as different elements of S have different F – images.
∴ F-1 exist and F-1 = {(3, a), (2, b), (1, c)}
∴ F1 T → S as defined by
F1 (3) = a, F-1 (2) = b, F1 (1) = c.
(ii) F (b) = 1, F (c) = 1 hence F (n1) = F (n2) ≠ n1, = n2
⇒ F is not one-one .: hence not invertible.
Question 12.
Consider the binary operations * : R x R → R and o : R x R → R defined as a* b = |a-b| and a o b = a, ∀ a, b ∈ R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that ∀ a, b, c ∈ R, a *(b o c) = (a * b) o (a * b). [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over? Justify your answer.
Answer:
∀ a, b ∈ R
a * b = |a – b| = |b – a| = b * a
hence commutative ∀ 3, 5 ,1 ∈ R
(3 * 5) * 7
|3 – 5| * 7 = 2 * 7= |2 – 7| = 5
3* (5 * 7) = 3* |5 – 7| =3 * 2= |3 – 2| = 1
a* (b * c) & (a * b) *c
∴ * is not associative.
a o b = a, b o a = b
hence a o b ≠ boa
hence not commutative
(a o b)o c : a o c = a
a o (b o c) = a o b = a
hence o is associative
a*(b o c) (a * b)=|a – b|
(a * b) o (a * c) = |a – b| o |a – c| = |a – b|
hence a* (b o c) = (a * b) o (a * c)
hence o is distributive over *.
![]()
Question 13.
Given a non-empty set X, let * : P(X) × P(X) → P(X) be defined as A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X). Show that the empty set φ) is the identity for the operation * and all the elements A of P(X) are invertible with A-1 = A.
(Hint: (A – ϕ) ∪ (ϕ – A) = A and (A – A) ∪ (A – A) = A * A = ϕ
Answer:
ϕ ∈ P (X) be an identity element.
To prove it let E ∈ P (X) be the identity element such that A * E = E * A = A
∀ A ∈ P (X)
(A – E) ∪ (E – A) = A ⇒ E = φ
i.e. (A – ϕ) ∪ (E – ϕ)) = A
A * ϕ = ϕ * A = A
* A = A, hence ϕ is the identity element.
Let Be P(X) be the inverse of A
∴ A* B = B * A = φ ∀ A e P(X)
(A – B) ∪ (B – A) = 0 ⇒ B = A
because A – B = ϕ B – A = ϕ⇒ A = B
∴ ∀ A ∈ P(X), A * A = ϕ
A is the invertible element of A
∴ A-1 = A
Question 14.
Define a binary operation * on the set {0, 1, 2, 3, 4, 5} as
\(\mathbf{a} * \mathbf{b}=\left\{\begin{array}{ll}{\mathbf{a}+\mathbf{b},} & {\text { if } \mathbf{a}+\mathbf{b}<\mathbf{6}} \\{\mathbf{a}+\mathbf{b}-\mathbf{6}} & {\text { if } \mathbf{a}+\mathbf{b} \geq \mathbf{6}}\end{array}\right.\)
Show that zero is the identity for this operation and each element a ±0 of the set is invertible with 6-a being the inverse of a.
Answer:
| * | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
From the composition table it is obvious that a
* 0 = a ∀ a ∈ {0, 1/2, 3,4, 5}
∴ 0 is the identity element
Also ∀ a ∈ {0, 1, 2, 3, 4, 5} ∃ (6 – a) ∈ {0,1,2, 3,4,5} such that
a * (6 – a) = (6 – a) * a = 0, a ≠ 0
hence 6 – a is the inverse of a .
However when a = 0, 6 – a g {0, 1, 2, 3,4, 5} hence 6 – a is the inverse of a when a ≠ 0.
Question 15.
Let A = {- 1, 0, 1, 2}, B = {- 4, – 2, 0, 2} and f, g : A → B be functions defined by
f (x) = x2 – x, x ∈ A and g (x) = -1, x ∈ A, Are f and g equal? Justify your answer.
(Hint: One may note that two functions f : A → B and g : A → B such that f(a) =
\(2\left|x-\frac{1}{2}\right|-1, x \in A A\), are called equal functions).
Answer:
f (-1) = (-1)2 + 1=2
f (0) = 02 – 0 = 0
f(1) = (1)2– 1 = 0
f(2) = (2)2 -2 = 2

Question 16.
Let A = {1, 2,3}. Then number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is
(A) 1
(B) 2
(C) 3
(D) 4
Answer:
R1 = {(1, 2), (1, 3), (1, 1), (2, 2), (3, 3), (3, 1), (2, 1)} is the only relation which is reflexive symmetric but not transitive and is such that {1, 2], {1, 3} ∈ R1 Correct answer is “A”
![]()
Question 17.
Let A = {1, 2, 3}. Then number of equivalence relations containing (1, 2) is
(A) 1
(B) 2
(C )3
(D) 4
Answer:
(i) {(1, 1), (1, 2), (2, 1), (2,2), (2, 3)}
(ii) {(1,1), (2,2), (3,3), (1,2), (2,1), (1,3), (3,1)} (2,3), (3,2)}
There are two equivalence relation
Correct answer is “B”.
Question 18.
Let f : R → R be the Signum Function defined as
\(\mathbf{f}(\mathbf{x})=\left\{\begin{array}{ll}{\mathbf{1},} {\mathbf{x}>\mathbf{0}} \\{\mathbf{0},} & {\mathbf{x}=\mathbf{0}} \\{-\mathbf{1},} & {\mathbf{x}<\mathbf{0}}\end{array}\right.\)
Answer:
fog (n) = f g(n) = f (0) = 0, 0 ≤ n < 1
f (1) = n = 1
gof (n) = g [1] = 1
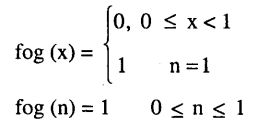
hence fog and gof does not coincide.
Question 19.
Number of binary operations on the set {a, b} are
(A) 10
(B) 16
(C) 20
(D) 8
Answer:
Number of Binary operation on a set {a, b} is
n (A) = 2 ∴ n(A×A) = 4
number of binary operation is 24 = 16.
correct answer is B.
2nd PUC Maths Relations and Functions Miscellaneous Exercise Additional Questions and Answers
One Mark Questions:
Question 1.
f: R → R defined by \(\left(f(x)=\left(3-x^{3}\right)^{\frac{1}{3}}\right.\) find fof (x) [CBSE 2010]
Answer:
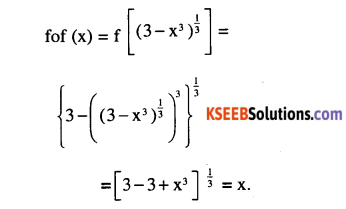
Question 2.
If \(\mathbf{f}(\mathbf{x})=\frac{1}{1-\mathbf{x}} \forall \mathbf{x} \in \mathbf{R}, \mathbf{n} \neq \mathbf{1}, \text { Find } \mathbf{f}[\mathbf{f}(\mathbf{f}(\mathbf{x}))]\)
Answer:

Question 3.
Let A = (1, 2, 3}, B = (4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A → B. State whether f is one-one or not f (1) = 4, f(2) = 5, f (3) = 6 [CBSE 2011]
Answer:
f (x1) = f(x2) → x1 = x2 ∀ n ∈ A
hence f is one-one.
![]()
Question 4.
* : R x R → R is a binary operation, a* b = 2a + b . Find (2* 3) * 4 [CBSE 2011]
Answer:
(2 * 3) *4 = (4 + 7) *4 = 11 * 4 = 26.
Question 5.
If \(f(n)=\frac{4 n+3}{6 n-4}, n \neq \frac{2}{3}\). show that f[f(n)]= n
Answer:

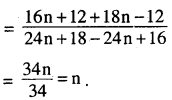
Four Marks Questions:
Question 1.
Show that the function f: R → R defined by \(f(n)=\frac{2 n-1}{3}, n \in R\) is one -one onto function .Also find the inverse of f.
Answer:

Question 2.
Let f : R → R defined as f(n) = 10n + 7 . Find the function g : R→ R such the
gof = fog = IR
Answer:
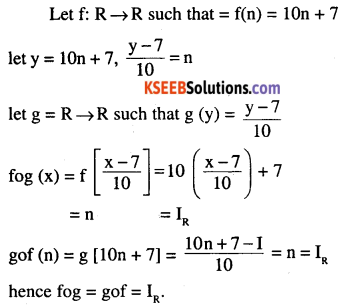
Question 3.
Show that f : A → B where A = (0,2 π) and B = [-1,1] such that fin) = sin n is not. invertible [I I T]
Answer:
\(\text { Let } n_{1}=\frac{\pi}{4}, \text { and } n_{2}=\frac{3 \pi}{4}\)
\(f\left(n_{1}\right)=\frac{1}{\sqrt{2}} f\left(n_{2}\right)=\frac{1}{\sqrt{2}}\)
f(n1) = f(n2) ⇒ n1≠ n2
hence it is not one-one
∀ y ∈ [-1, 1] ∃ n ∈ (0, 2π) such that f (n) = sin n
hence f is onto
since f is not one-one.
It is not invertible.
Question 4.
Is the function sin (sin1 n) bijective? [I I T] Which is defined on [-1, 1] to [-1, 1].
Answer:
Let f (n) = sin (sin-1 n)
let n1 n2 ∈ [-1, 1]
f (n1) = f (n2) ⇒ sin (sin-1 n1) = sin [sin1 (n2)]
⇒ n1 = n2
hence f is one-one
let y = sin (sin-1 n) = n
∀ y ∈ [-1,1] ∃ [-1, 1] f(n) = n
hence f is onto
since f is one-one and onto it is bijective.
![]()
Question 5.
If f be greatest integer function and g be the absolute function. Find
\(fog\left( \cfrac { -3 }{ 2 } \right) +gof\left( \cfrac { 4 }{ 3 } \right) \) [CBSE 2007]
Answer: