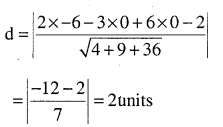Students can Download Maths Chapter 11 Three Dimensional Geometry Ex 11.3 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 11 Three Dimensional Geometry Ex 11.3
2nd PUC Maths Three Dimensional Geometry NCERT Text Book Questions and Answers Ex 11.3
Question 1.
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin,
(a) z = 2
Answer:
Z = 2
ax + by + cz = P
ox + oy + 1z = 2
Directions = 0,0,1
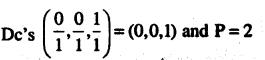
(b) x + y + z = 1
Answer:

(c) 2x + 3y – z = 5
Answer:

(d) 5y + 8 = 0
Answer:
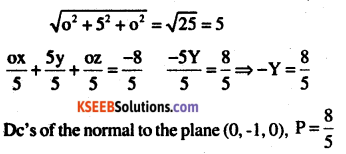
![]()
Question 2.
Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector \(3 i+5 j-6 \hat{k}\)
Answer:

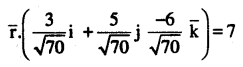
Question 3.
Find the Cartesian equation of the following planes:
(a) \(\overrightarrow{\mathrm{r}} \cdot(\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}})=2\)
Answer:
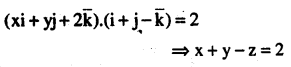
(b) \(\overrightarrow{\mathbf{r}} \cdot(2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}-4 \hat{\mathbf{k}})=\mathbf{1}\)
Answer:
2x + 3y +4z = 1
(c) \(\overrightarrow{\mathbf{r}} \cdot[(\mathbf{s}-2 \mathbf{t}) \hat{\mathbf{i}}+(\mathbf{3}-\mathbf{t}) \hat{\mathbf{j}}+(2 \mathbf{s}+\mathbf{t}) \hat{\mathbf{k}}]=\mathbf{1} \mathbf{5}\)
Answer:
x(s – 2t) + y((3-t) +z(2s +t) = 15
![]()
Question 4.
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
(a) 2x + 3y + 4z – 12=O
Answer
Direction ratio of any line normal to
2x + 3y + 4z – 12 = O is (2,3,4)
∴ Equation of line through (O, O, O) and is ‘⊥’ to given lines is
\(\frac{x-0}{2}=\frac{y-0}{3}=\frac{z-4}{4}\)
any point on the lines is (2λ, 3λ, 4λ) but this lines on the given plane

(b) (1, 1, 0), (1, 2, 1), (- 2, 2, – 1)
Answer
The given equation passes through (1,1,0) equation of plane is (0, 3 , 4)
Equation of a lines through the orgin and is ‘⊥’ to given lines is
\(\frac{x-0}{0}=\frac{y-0}{3}=\frac{z-0}{4}=\lambda\) and any points on the line is (0, 3λ, 4λ) but this point lines on the given plane.
Answer:

(c) x + y + z = 1
Answer
Direction of any line normal to the given plane is (1,1,1)
Equation of a lines through (0,0,0) and is ‘⊥’ to the given lines is
\(\frac{x-0}{1}=\frac{y-0}{1}=\frac{z-0}{1}=\lambda\)
any point on this line (λ,λ,λ) but this point lies on the plane x +y + 2 = 1
\(\lambda+\lambda+\lambda=1 \Rightarrow \lambda=\frac{1}{3}\)
\( \text { foot of perpendicular is }\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)\)
(d) 5y + 8 = 0
Answer:
Directions of normal to the plane is (0,5,0) equation of a line through (0,0,0) and ‘⊥’ to the plane is \(\frac{x-0}{0}=\frac{y-0}{5}=\frac{z-0}{0}=\lambda\)
any point on this line is (0,5λ,0) but this point lines on the plane

Question 5.
Find the vector and cartesian equations of the planes
(a) that passes through the point (1, 0, – 2) and the normal to the plane is \(\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}\)
Answer:
Equation of plane through \(\overline{\mathbf{a}}\) and normal to \(\overline{\mathbf{x}} \) is of the form \((\overline{\mathbf{r}}-\overline{\mathbf{a}}) \cdot \overline{\mathbf{x}}=\mathbf{0}\)
\([(x i+y j+z \bar{k})-(i+0-2 j)] \cdot[i+j-\bar{k}]=0\) which is the vector equation
(x – 1) x 1 + y x 1 + (z + 2) (- 1 ) = 0
x + y- z- 3 = 0 which is cartesian equation.
![]()
(b) that passes through the point (1,4, 6) and the normal vector to the plane is
\(\hat{\mathbf{i}}-2 \hat{\mathbf{j}}+\hat{\mathbf{k}}\)
Answer:

Question 6.
Find the equations of the planes that passes through three points.
(a) (1, 1, – 1), (6, 4, – 5), (- 4, – 2, 3)
Answer:
Equation of plane is 3 point form is

plane is 0 mean the plane is not fixed by the given points. That is points are collinear.
(b) (1, 1, 0), (1, 2, 1), (- 2, 2, – 1)
Answer:
The given equation passes through (1,1,0) equation of plane is
(x-1) + b (y – 1) + c (z-0) = 0
but this plane passes through (1,2, 1)
a (1 – 1) + b (2 – 1) + c (1- 0)
= 0 b + c = 0 → (1)
also it passes through (-2, 2,-1)
a (-2 -1) + b (2 – 1) + c (-1 – 0)
= 0 -3a + b – c = 0 → (2)
solving (1), (2)

∴ equation of plane
(x -1) + (y – 1) -3 (z – 0) = 0
2x + 3y – 3z – 5 = 0
[Note: Part (a) and part (b) are of same type question but in two different method. However students can choose any one method according to their wish.]
![]()
Question 7.
Find the intercepts cut off by the plane 2x + y – z = 5.
Answer:

Question 8.
Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane. Answer:
Equation of ZOX plane is y = 0
Direction ratio of normal to this plane is (0,1,0)
since the required plane is parallel to y = 0
Direction ratio of its normal is also (0,1,0).
Intercepts on y-axis is 3,
∴ The point (0, 3,0) lies on the plane.
∴ equation of plane
(x – 0) + 1 (y – 3) + 0 (z – 0) = 0
∴ y = 3.
Question 9.
Find the equation of the plane through the intersection of the planes 3x-y + 2z-4 = 0 and x + y + z- 2 = 0 and the point (2,2,1).
Answer:
Let the plane be
P1 : 3x – y + 2z – 4 = 0,
P2 : x + y – z – 2 = 0
plane through the intersection be P1 + λ P2 =0
(3x – y + 2z – 4) +λ (x + y + z – 2) = 0
but it passes through (2,2,1)
6 – 2+ 2 – 4) + X (2 + 2 + 1 – 2) = 0 ⇒ 2 + 3λ = 0
\(\lambda=\frac{-2}{3}\)
∴ Equation of plane is
\((3 x-y+2 z-4)+\frac{-2}{3}(x+y+z-2)=0\)
9x – 3y + 6z – 12 – 2x – 2y -2z + 4 = 0
7x – 5y + 4z – 8 = 0
Question 10.
Find the vector equation of the plane passing through the intersection of the planes
\(\overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}})=7, \overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})=9 \) and through the point (2,1,3).
Answer:
Let the planes be
P1 : 2x + 2y -3z – 7 = 0,
P2 : 2x +5y + 3z = 9
∴ Required equation be P1 + λ P2 = 0
(2x + 2y – 3z – 7) + λ (2x + 5y + 3z – 9) = 0,
passes through (2, 1, 3)
(4 + 2 – 9 – 7) + λ (4 + 5 + 9 – 9) = 0
\(-10+\lambda 9=0 \quad \Rightarrow \lambda=\frac{10}{9}\)
Required plane is
(2x + 2y – 3z – 7) + λ (2x + 5y + 3z – 9) = 0
18x + 18y -27z – 63 + 20x + 50y + 50z – 90 = 0
38x + 68y + 3z – 153 = 0
![]()
Question 11.
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
Answer
Let P1 : x + y + z – 1 = 0 and
P2 : 2x + 3y + 4z -5 = 0
Equation of plane is P1 + λ P2 = 0
(x + y + z – 1) + λ (2x + 3y + 4z – 5) = 0
x (1+2λ) + y(1+ 3X) +z(1 + 4),)-1 -5λ = 0
Dr’s of the normal to the plane is …
1+ 2λ ,1+3λ ,1+4λ
since the plane is ‘⊥’ to x – y + z = 0
(1 + 2λ) (1) + (1+3λ) (-1) + (1+4λ) 1= 0

Question 12.
Find the angle,between the planes whose vector equations are
\(\overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}})=5 \text { and } \overrightarrow{\mathrm{r}} \cdot(3 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}+5 \hat{\mathrm{j}}+5 \hat{\mathrm{k}})=3\)
Answer:
Dr’s of the normal to the planes are (2,2,-3) and (3,-3, 5)
Let θ be angle between them

Question 13.
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 7x + 5y + 6z + 30 = 0 and
3x – y – 10z + 4 = 0
Answer
Dr’s of the normal to the planes are (7,5,6) and (3,-1,-10) since Dr’s are neither proportional nor the product = 0
They are neither parallel nor ‘⊥’. Hence they interset.
Let θ be the angle between them

![]()
(b) 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
Answer
Dr’s are (2,1,3), (1,-2, 0)
since product of direction
∴ 2 x 1 + 1 x -2 + 3 x 0 = 0
planes are perpendicular. (θ= 90°)
(c) 2x – 2y + 4z + 5 = 0 and
3x – 3y + 6z – 1 = 0
Answer
Dr’s are (2,-2,4)), (3, -3, 6)
\(\frac{2}{3}=\frac{-2}{-3}=\frac{4}{6} \Rightarrow \frac{2}{3}=\frac{2}{3}=\frac{2}{3}\)
Since Dr’s are proportional, planes are parallel. (θ = 0°)
(d) 2x – y + 3z – 1 = 0 and
2x – y + 3z + 3 = 0
Answer
Dr’s are (2,-1,3), (2,-1,3)
Since Dr’s are proportional, planes are parallel. (θ = 0°)
\(\frac{2}{2}=\frac{-1}{-1}=\frac{3}{3} \Rightarrow 1=1=1\)
Since Dr’s are proportional, planes are parallel. (θ = 0°)
(e) 4x + 8y + z – 8 = 0 and y + z – 4 = 0
Answer
Dr’s are (4,8,1), (0, 1, 1)
Dr’s are neither proportional nor the product = 0
hence they intersect.
Let θ be the angle between them.

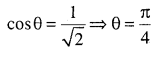
Question 14.
In the following cases, find the distance of each of the given points from the
corresponding given plane.
Point Plane
(a) (0, 0, 0), 3x – 4y + 12 z = 3
Answer:
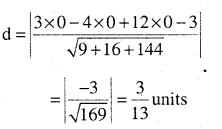
(b) (3,-2,1), 2x – y + 2z + 3 = 0
Answer:
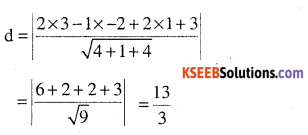
(c) (2, 3,-5), x + 2y – 2z = 9
Answer:
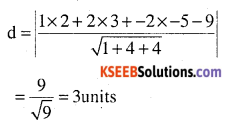
(d) (- 6, 0, 0) 2x – 3y + 6z – 2 = 0
Answer: