Students can Download 2nd PUC Physics Previous Year Question Paper March 2019, Karnataka 2nd PUC physics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Physics Previous Year Question Paper March 2019
Time: 3 Hrs 15 Min
Max. Marks: 70
Introductions:
- All parts are compulsory.
- Answer without relevant diagram/figure/circuit wherever necessary will not carry any marks.
- Numerical problems solved without writing the relevant formulae carry no marks.
Part – A
I. Answer the following questions in one sentence each: ( 10 × 1 = 10 )
Question 1.
State Coulomb’s Law.
Answer:
Coulomb’s law states that force of attraction or repulsion between two point charges is directly proportional to product of two charges and inversely proportional to square of distance between them.
Question 2.
Define electrical resistivity of material of a conductor.
Answer:
Electrical resistivity of material of a conductor is the resistance of the conductor per unit length and per unit area of given material of conductor.
Question 3.
Write the expression for force acting on a moving charge in a magnetic field.
Answer:
F = q(\(\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}}\)) or F = gVBsinθ.
Question 4.
What is magnetic susceptibility?
The ratio of magnetization to magnetic intensity is called magnetic susceptability.
X = \(\frac{M}{H}\)
Question 5.
How the self inductance of a coil depends on number of turns in the coil.
Self inductance of a coil is directly proportional to square of number of turns.
L ∝ n2.
Question 6.
For which position of the object magnification of convex lens is -1. (minus one)?
Answer:
Twice the focal length from the line or
R = 2f
![]()
Question 7.
For which angle of incidence reflected ray is completely polarised?
Answer:
Brewster’s angle or polarizing angle.
Question 8.
Mention any one type of electron emission.
Answer:
Thermionic emission (field / photoelectric / secondary).
Question 9.
Write the expression for energy of an electron in electron orbit of hydrogen atom.
Answer:
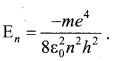
Question 10.
Write the relation between Half-Life and Mean-Life of radio active element.
Answer:
T1/2y = 0.693 τmean.
Part – B
II. Answer any five of the following questions: ( 5 × 2 = 10 )
Question 11.
Write any two basic properties of charge.
Answer:
- Like charges repel and unlike charges attract each other.
- Electric charge is additive in nature.
- The electric charge is conserved.
- The electric charge is quantized.
- Charges are not affected by the motion of the body.
Question 12.
Write the expression for drift velocity interms of current, explain the terms used.
Answer:
Vd = \(\frac{\mathrm{I}}{n \mathrm{A} e}\)
Where, I – current
n – number of electrons per unit volume.
A – area of cross section.
e – charge on electron
Question 13.
Define magnetic ’dip’ and ‘declination’ at a place.
Answer:
Magnetic dip : The angle made by the earth’s magnetic field with its horizontal component is called magnetic dip.
Magnetic declination: The angle between magnetic meridian and geographic meridian is called magnetic declination.
Question 14.
Write the expression for speed of light in terms of “µ0 ” and “∈0“, explain the terms used.
Answer:
Velocity of light, c = \(\frac{1}{\sqrt{\mu_{0} \epsilon_{0}}}\)
µ0 = Permeability of free space,
∈0 = Permittivity of free space.
Question 15.
Write the ray diagram for formation of image in the simple microscope.
Answer:
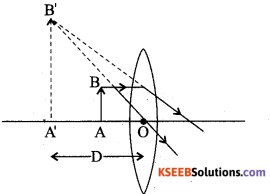
Question 16.
What is diffraction of light?
Answer:
The phenomenon of bending of light around the comers of (edges of) small obstacles or apertures and spreading into geometrical shadow region is called diffraction of light.
Question 17.
Write the expression for de-Broglie wave length of electrons interms of electric potential and explain the terms used.
Answer:
We know that the wavelength associated with the accelerating electron,

Hence λc ∝ \(\frac{1}{\sqrt{V}}\) where V= is the electric potential.
Question 18.
Distinguish between n-type and p-type semi conductors.
Answer:
p-type:
- p-type semiconductor is obtained by doping a trivalent impurity to a pure semi conductor.
- Number of holes is greater than number of electrons i.e. nh > ne
- holes-majority carriers.
- electrons-minority carriers.
- trivalent doping provides one hole for conduction.
- Impurity is called acceptor type.
n-type:
- n-type semiconductor is obtained by doping a pentavalent impurity to a pure semiconductor.
- Number of holes is less than number of electrons nh < ne
- holes-minority carriers.
- electrons-majority carriers.
- Pentavalent doping provides one extra electron for conduction.
- Impurity is called donor type.
Part – C
III. Answer any five of the following questions. ( 5 × 3 = 15 )
Question 19.
Derive an expression for potential energy of electric-dipole placed in an uniform electric field.
Consider an electric dipole of dipole moment \(\overrightarrow{\mathrm{p}}\) = q (2\(\overrightarrow{\mathrm{a}}\)) placed at an angle 0 in the direction of uniform electric field \(\overrightarrow{\mathrm{E}}\).
The dipole experiences torque τ = P x E = pE sinθ
This torque tends to rotate the dipole in the direction of the electric field.
Suppose an external torque τext is applied just to neutralise the torque (τ) and to rotate the dipole from θ0 to θ1 without angular acceleration then, the amount of work done by the external torque.
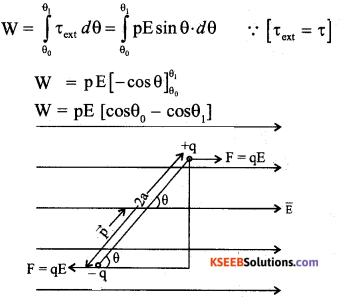
The work done in rotating the dipole from a position of zero potential energy (θ0 = \(\frac{\pi}{2}\) ) to any given position in the field ( θ1 = θ then,
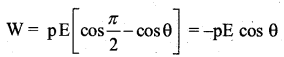
This quantity of work done is stored as potential energy U.
Thus, potential energy of an electric dipole
in a uniform Electric field is U = -pE cosθ
= \(-\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{E}}\)
Question 20.
Write the,expression for force per unit length between two straight parallel current carrying conductors of infinite length. Hence define SI unit of current ’ampere’.
Answer:

One ampere is that steady current through each of infinitely long straight parallel conductors of negligible area of cross section separated by a distance of lm in vacuum, then each experience a force of 2 × 10-7 Nm-1.
Question 21.
Distinguish between ’dia’ and ’ferro’ magnetic materials.
Answer:
Diamagnetic material
- Weakly repelled by magnetic
- When placed in a magnetic field it is weakly magnetized in a direction opposite to that of applied field.
- µr is sightly less than 1
- When placed in a magnetic field flux density (B) inside the material is less than in air.
- Xm (susceptibility) doesnot change with temperature.
- Intensity of magnetization a small and negative value.
- Xm has small negative value.
![]()
Ferromagnetic material
- Strongly attracted by magnetic field
- it is strongly magnetized in the direction of applied field.
- When placed in a magnetic field the flux density (B) inside the material is much large than in air.
- Xm decreases with rise temperature.
- I has large positive value.
- Xm has very high positive value.
Question 22.
Mention the three types energy loss in a transformer.
Answer:
- Loss due to heating
- Loss due to flux leakage
- Loss due to eddy currents
- Hysteresis loss.
Question 23.
Write three experimental observations of photoelectric effect.
Answer:
The results of the experimental studies of photoelectric effect are sometimes called as the laws of photoelectric effect.
1. The photoelectric effect is instantaneous, i.e., photoelectric current flows as soon as the radiation falls on the cathode (about 10-9s).
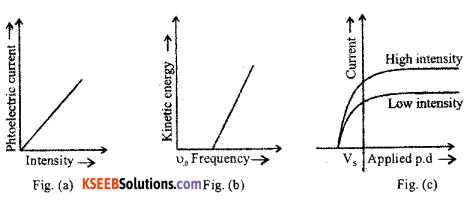
2. The strength of photo electric current is directly proportional to the intensity of incident radiation (Fig. a).
3. For a given photo emissive surface there is a minimum frequency for the incident radiation below which there is no photoelectric emission. This minimum frequency is called threshold frequency υ0 (Fig. b).
4. Above threshold frequency, the maximum kinetic energy of the photoelectrons increases linearly with the frequency of the incident radiation (Fig. b).
5. As the applied potential is increased the photoelectric current increases and attains saturation. On reversing the potential, photo current decreases and becomes zero at a particular negative potential and is called stopping potential Vs (Fig. c).
Question 24.
Write the three postulates of Bohr’s atomic model.
Answer:
- An electron in an atom could revolve around the nucleus only in certain stable orbits without the emission of radiant energy.
- An electron revolves around the nucleus only in those orbits for which the angular momentum is an integral multiple of (h / 2 π), where h is the Planck’s constant.
- An electron can jump from higher energy orbit to lower energy orbit. In this process a photon is emitted whose energy is equal to the energy difference between the initial and final states.
Question 25.
Explain ‘Conduction band’ ‘Valance band’ and ‘Energy gap’, in semiconductors.
Answer:
Conduction band : The band lying next to the valence band which may be partially filled at room temperature but completely empty at OL is called conduction bond. Electrons in this band contribute to the conduction process. Hence the conductivity of a solid depends on the availability of electrons in the conduction band. Electrons in thi s band is called conduction electrons.
Valance band : The highest energy band which is completely or partially filled at absolute zero (OK) is called valance band. Electrons in this band are called valance electrons. They are loosely bound to the nucleus. They are easily detachable from the nucleus.
Energy gap : The separation between the top of the valance band and bottom of the conduction band is called energy gap. This is so called because electrons cannot possess these energy levels in the given solid.
Question 26.
What is modulation? Write the block diagram of the receiver.
Modulation is the process of superposing modulating audio signal on a high frequency carrier wave

Part – D
IV. Answer any two of the following questions: ( 2 × 5 = 10 )
Question 27.
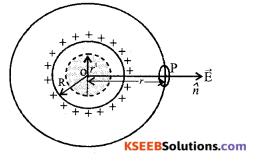
State Gauss’s law. Derive an expression for electric intensity at a point outside the uniformly charged shell.
Answer:
Consider a charged thin spherical shell of radius R. Let the charge +q distribute uniformely on the outer surface of the conductor, so that the surface charge density be ‘σ’
Case 1: Outside the spherical shell:
Let ‘P’ be a point outside the conductor at a distance r from the centre of the spherical shell.
With ‘r ’ as the radius imagine a Gaussian surface. The electric field at every point on the Gaussian surface is same and radial (θ = 0).
The flux through the Gaussian surface of radius r is
Φ = E.S cosθ S – Surface
area of the Gaussian surface of radius r.
∴ Φ = E . (4πr2)………………(1)
From Gauss’s Law Φ = \( \frac{q}{\varepsilon_{0}}\) ……………….(2)
Equating (1) and (2), we get
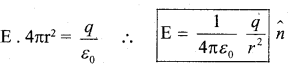
\(\hat{n}\) – Unit radial vector
Case 2: On the surface of the spherical shell:
The electric field on the surface of the conductor r = R, then
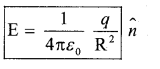
Case 3: Inside the spherical shell: Since the charges enclosed by the Gaussian surface of radius (r ‘) is zero, the electric field inside the spherical shell is zero.
Question 28.
Two cells of emf E1 and E2 and internal resistance r1, and r2 are connected in parallel such that they send current in same direction. Derive an expression for equivalent resistance and equivalent emf of the combination.
Answer:
Consider two cells of emf and ε1, ε2, with internal resistances and r1 and r2 connected in parallel. Let I1 and I2 be the currents through the cell ε1 and ε2 respectively.
then I = I1 + I2 ………………….(1)
The potential difference across ε1
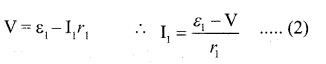
Potential differences across ε2
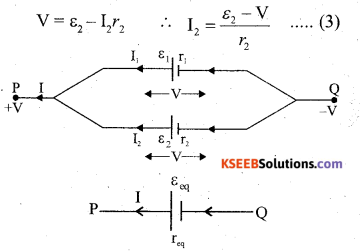
Substituting in eqn (1)


![]()
Question 29.
Derive an expression for the intensity of magnetic field at any point on the axis of a circular current loop.
Answer:
Consider a circular current loop of radius R carrying steady current I. Let ‘P’ be a point on the axis at a distance x from the centre of the loop.
To find the magnetic field at ‘P’ due to the current loop, consider a small current element
AB (I. \(\overrightarrow{\mathrm{d} l}\) ) on the loop.
The magnetic field at ‘P’ due to the current element AB is given by Biot Savart’s Law
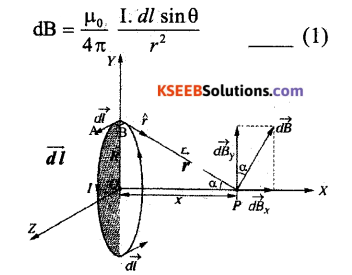
Since the current element (I. \(\overrightarrow{\mathrm{d} l}\) ) and the
displacement vector \(\vec{r}\) are perpendicular to each other, then θ = 90° (sin 90 = 1)
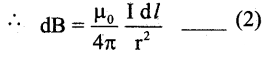
The direction of dB is perpendicular to the plane of I dl and \(\vec{r}\).
Let dB make an angle a with y axis then resolving dB,
We get dBx = dB sinα and dBy = dB cosα This perpendicular component of magnetic field(dBy) will concel because of the equal and opposite perpendicular component from diametrically opposite current element.
∴ Resultant magnetic field at P is

V. Answer any two of the following questions: ( 2 × 5 = 10 )
Question 30.
Derive an expression for the impedance of a series LCR circuit, when an AC voltage is applied to it.
Consider a resistance R, an inductor of self inductance L and a capacitor of capacitance C connected in series across an AC source. The applied voltage is given by,
v = v0sinωt ……(1)
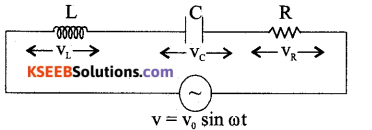
Where, v is the instantaneous value, v is the peak value and ω = 2πf, f being the frequency of AC.
If i be the instantaneous current at time t, the instantaneous voltages across R, L and C are respectively iR, iXL and iXC. The vector sum of the voltage amplitudes across R, L, C equals the amplitude v0 of the voltage applied.
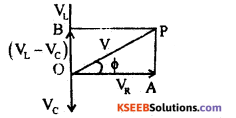
Let vR, vL and VC be the voltage amplitudes .across R, L and C respectively and I0 the current amplitude. Then vR = I0R is in phase with i0.
vL = i0XL = I0(ωL) leads i0 by 90°
vc = i0Xc = i0 (\(\frac{1}{\omega C}\)) lags behind io by 90°
The current in a pure resistor is phase with the voltage, whereas the current in a pure inductor lags the voltage by \(\frac{\pi}{2}\) rad. The current in a pure capacitor leads the voltage by \(\frac{\pi}{2}\) rad.
For vL > vc , phase angle Φ between the voltage and the current is positive.
From the right angled triangle OAP,
OP2 = OA2 + AP2 = OA2 + OB2 (Q AP= OB)
v2 = v2R + (VL – Vc)2 = (iR)2 + (iXL – iXc)2
=i2 (R 2+ (XL – Xc)2)
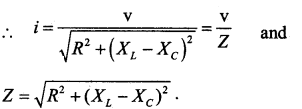
Where Z is the impedance of the circuit. Phase angle between v & i.
![]()
Question 31.
Derive “Lensmaker’s” formula.
Answer:
Lens maker’s formula.
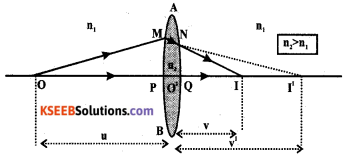
Let r1 and r2 be radii of curvature of the thin lens.
Let O be the point object at a distance u from the pole of the first curved surface of the lens. Real image is formed at 1’, at a distance v’ from the pole P1 This image is formed in the denser medium.
We know that from the refraction formula,
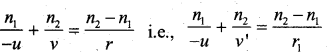
Where n1 is the refractive index of rarer medium and that of the denser medium (n2 > n1). For the second surface, real image at I’ will serve as a virtual object and the distance is taken as -ve. The object space is he lens medium for refraction through the second curved surface. Final image is formed in air at I and at a distance of V and P2.

∴The term on the L.H.S. can be replaced by 1/f where f is the focal length of lens.
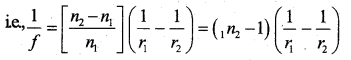
The equation (4) is called the lens maker’s formula.
![]()
Question 32.
Explain the working of a n-p-n transistor in CE mode as an amplifier.
Answer:
The circuit diagram of a CE amplifier using npn transistor is as shown in figure.
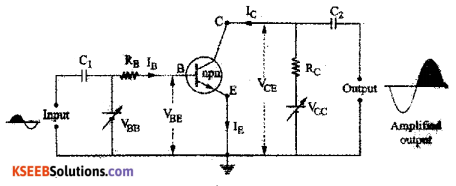
The input (base emitter) circuit is forward biased and the output (collector emitter) circuit is reverse biased.
When the ac input signal to be amplified is fed to the base-emitter circuit. The output voltage Vo varies in accordance with the relation, Vo = VCE = VCC – ICRC. These variations in the collector voltage VCE appears as amplified output.
During the positive half cycle of ac input signal, the forward bias of emitter base junction increases. Due to this base current IB increases and hence collector current IC increases. As a result of this ICRC increases. Therefore the output voltage Vo is negative. This indicates that the positive half cycle of input ac signal voltage is amplified through negative half cycle.
During the negatice half cycle of ac input signal, the forward bias of emitter base junction decreases. Due to this base current IB decreases and hence collector current Ic decreases. As a result of this ICRC decreases. Therefore the output voltage Vo is positive. This indicates that the negative half cycle of input ac signal voltage is amplified through positive half cycle.
Thus, the weak input signal is amplified and output signal is out of phase with the input signal by 180°.
VI. Answer any three of the following questions : ( 3 × 5 = 15 )
Question 33.
In a circular parallel plate capacitor radius of each plate is 5 cm and they are separated by a distance of 2 mm. Calculate the capacitance and the energy stored, when it is charged by connecting the battery of 200 V (given ∈0 = 8.854 × 10-12Fm-1).
Solution:
Given: r = 5 cm, 5 × 10-2m, d = 2 × 10-3m, V = 200 V, ∈0= 8.854 × 10-12Fm-1
Area of circle, A = πr2
= 3.14 × (5 × 10-2)2
A = 78.5 × 10-4m2

C = 347.5 × 10-13F
Energy stored in a capacitor
U= \(\frac{1}{2}\) CV2 = \(\frac{1}{2}\) × 347.5 × 10-13 × (200)2
= 6950390 × 10-13
U = 6.95 × 10-7J
Question 34.
Two resistors are connected in series with 5V battery of negligible into nal resistance. A current of 2 A flows through each resistor. If they, are connected in parallel with the same battery’ a current of \(\frac{25}{3}\) Allows through combination. Calculate the value of each resistance.
Solution:
Given: R1 = ?, R2 = ?
In series: R1 + R2 = RS
Rs = \(\frac{V}{I}=\frac{5}{2}\) = 2.5Ω
R1 + R2 = Rs = 2.5Ω ….. (1)
In parallel:
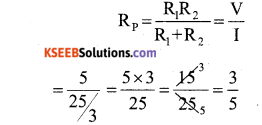
Rp = 0.6Ω
Rp = \(\frac{\mathrm{R}_{1} \mathrm{R}_{2}}{\mathrm{R}_{1}+\mathrm{R}_{2}}\)
From 1
Rp = \(\frac{R_{1} R_{2}}{2.5}\)
= 0.6 × 2.5 = R1R2
R1R2= 1.5Ω
(R1 – R2)2 = (R1 + R2)2 – 4R1R2
= (2.5)2 – 4 × 1.5
= 6.25 – 6
R1 – R2 = √0.25
R1 – R2 = 0.5 ………. (2)
Solve (1) and (2)
R1 + R2 = 2.5
R1 – R2 = 2.5
2R1 = 3
R1= \(\frac{3}{2}\) = 1.5Ω
From (1), we can write,
R1 + R2 = 2.5
1.5 + R2 = 2.5
R2 = 2.5 -1.5
R2 = 1Ω
Question 35.
A conductor of length 3m moving in a uniform magnetic field of strength 100 T. It covers a distance of 70 m in 5 sec. Its plane of motion makes an angle of 30° with direction of magnetic field. Calculate the emf induced in it.
Answer:
Given: l = 3m, B = 100T, d = 70 m, t= 5 sec., θ = 30°, e = ? e = BlVsinθ
V = \(\frac{d}{t}=\frac{70}{5}=14 \mathrm{m} / \mathrm{s}\)
V = 100 × 3 × 14 × sin 30° = 100 × 3 14 × \(\frac{1}{2}\)
e = 2100 V
![]()
Question 36.
In a Young’s double slit experiment wave length of light used is 5000 Å and distance between the slits is 2 mm, distance of screen from the slits is 1 m. Find fringe width and also calculate the distance of 7th dark fringe from central bright fringe.
Answer:
λ = 5000Å , d = 2mm = 2 × 10-3m, D = 1m, (β = ?, n = 7
(i) Fringe width,
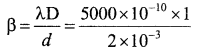
β = 2.5 × 10-4 m
(ii) Distance of 7th dark fringe from central bridge fringe
n = 6
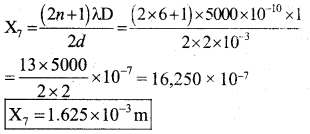
Question 37.
Half life of U-238 undergoing a-decay is 4.5 × 109 years. What is the activity of one gram of U-238 sample?
Answer:
T1/2 =4.5 × 109 years
= 4.5 × 109 × 365 × 24 × 60 × 60
T1/2 = 1.419 × 1017nsec.
Number of atoms in lg of U-238
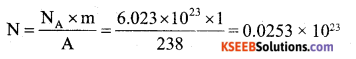
N = 2.53 × 1021
Decay rate or activity A = λN but

A = 1.235 × 104Bq