KSEEB Solutions for Class 8 Maths Chapter 13 Statistics Ex 13.3

Students can Download Maths Chapter 13 Statistics Ex 13.3 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka Board Class 8 Maths Chapter 13 Statistics Ex 13.3

Question 1.
Runs scored by 10 batsmen in a one-day cricket match are given. Find the average run scored. 23, 54, 08, 94, 60, 18, 29, 44, 05, 86
Answer:
Σ x = 23 + 54 + 08 + 94 + 60 + 18 + 29 + 44 + 05 + 86 = 421
N = 10
Average = Mean = \overline{X}=\frac{\Sigma x}{N}=\frac{421}{10}=42.1

Question 2.
Find the mean weight form the following table:

Weight (kg) 29 30 31 32 33
No. of children 02 01 04 03 05

Answer:

Weigh t(kg) No. of children(x) ‘ f
29 02 58
30 01 30
31 04. 124
32 03 96
33 05 164
N= 15 Zf = 473

Mean = \(\frac{\Sigma f_{X}}{N}=\frac{473}{15}=31.53\)

Question 3.
Calculate the mean for the following frequency distribution.

Mark 10-20 20-30 30-40 40-50 50-60 60-70 70-80
Frequency 3 7 10 6 8 2 4

Answer:

Marks Frequency Midpoint fx
10-20 3 15 45
20-30 7 25 175
30-40 10 35 350
40-50 6 45 270
50-60 8 55 440
60-70 2 65 130
70-80 4 75 300
N = 40 Efx = 1710

Mean = \(\frac{\Sigma f_{x}}{N}=\frac{1710}{40}=42.75\)

Question 4.
Calculate the mean for the following frequency distribution.

Mark 15-19 20-24 25-29 30-34 35-39 40-44
Frequency 6 5 9 12 6 2

Answer:

Marks. Frequency Midpoint f(X)
15-19 6 17 102
20-24 5 22 *110
25-29 9 27 243
30-34 12 32 384
35-39 6 37 222
40-44 2 42 84
N = 40 Efx = 1145

Mean = \(\overline{X}=\frac{\Sigma f_{X}}{N}=\frac{1145}{40}=28.625\)

Question 5.
Find the median of the data 15,22, 9,20, 6,18,11,25,14.
Answer:
6, 9, 11, 14,(15), 18, 20, 22,25 (Ascending order)
N = 9,
\frac{N+1}{2}+\frac{9+1}{2}=\frac{10}{2}=5^{\text { th }}
Median = 15.

Question 6.
Find the median of the data 22,28,34, 49, 44, 57,18,10,33, 41, 66, 59.
Answer:
10, 18, 22, 28, 33, 34, 41, 44, 49, 57, 59, 66 (Ascending order)
N = 10
∴ Median = \frac{34+41}{2}=\frac{75}{2}=37.5

Question 7.
Find the median for the following frequency distribution table.

Class interval 110-119 120-129 130-139 140-149 150-159 160-169
Frequency 6 8 15 10 6 5

Answer:

Class interval Frequency (f) Cumulative frequency (fc)
110-119 6 6
120-129 8 14
130-139 15 29
140-149 10 45
160-169 5 50
 N = 50

N = 50
\(\frac{\mathrm{N}}{2}=\frac{50^{25}}{\not 2}=25\)
∴ Median class is 130 – 139
LRL = 129.5
Fc = 14
Fm = 15
i = 10
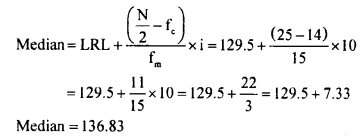
KSEEB Solutions for Class 8 Maths Chapter 13 Statistics Ex. 13.3 1

Question 8.
Find the median for the following frequency distribution table.

Class interval 0-5 5-10 10-15 15-20 20-25 25-30
Frequency 5 3 9 10 8 5

Answer:

Class interval Frequency (t) Cumulative frequency (fc)
0-5 5 5
5-10 3 8
10-15 9 , 17
15-20 10 27
20-25 8 35
25-30 5 40
N = 40

N = 40
\(\frac{N}{2}=\frac{40}{2}=20\)
∴ Median class is 15 – 20
LRL = 15
Fc = 17
Fm = 9
i = 5
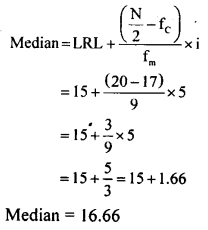
KSEEB Solutions for Class 8 Maths Chapter 13 Statistics Ex. 13.3 2

Question 9.
Find the mode for the following data.
(i) 4,3,1,5,3, 7, 9,6 Answer: Mode = 3
(ii) 22,36,18,22,20,34,22, 42, 46,42
Answer:
Mode = 22

Question 10.
Find the mode for the following data

X 5 10 12 15 20 30 40
f 4 8 11 13 16 12 9

Answer:
Mode = 20 (It has the highest frequency)