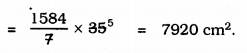Karnataka Board Class 9 Maths Chapter 13 Surface Area and Volumes Ex 13.2
(If values are not given for ‘π’ Assume π = \(\frac{22}{7}\))
Question 1.
The curved surface area of a right circular cylinder of a height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Solution:
Lateral surface area of cylinder which has height 14 cm is 88 cm2.
Diameter of bottom of cylinder, d = ?
h = 14 cm, L.S.A. = 88 cm2, d = ?
Lateral surface area of cylinder, L.S.A.
L.S.A.= 2πrh = 88
![]()
88 × r = 88
∴ r = \(\frac{88}{88}\) ∴ r = 1 cm.
∴ Diameter, d = 2r =2 × 1 = 2 cm.
Question 2.
It is required to make a closed cylinderical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square metres of the sheet are required for the same ?
Solution:
Height of cylindrical water tank, h = 1 m
Diameter of bottom, d = 140 cm.
h = 1 m, d = 140 cm,
![]()
r = 0.7 m.
Area of metal sheet required to prepare water tank, A
A = 2πr (r + h)
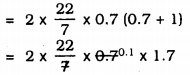
= 44 × 0.1 × 1.7
= 4.4 × 1.7
A = 7.48 m2.
Question 3.
A metal pipe is 77 cm long. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm (see Fig. 13.11). Find its
(i) inner curved surface area,
(ii) outer curved surface area,
(iii) total surface area.
![]()
Solution:
Length of metal pipe, l = 77 cm,
h = 77 cm.
Inner diameter = 4 cm, ∴ r1 = 2 cm.
Outer diameter= 4.4 cm. ∴ r2 = 2.2 cm.
(i) Inner surfce area of pipe (C.S.A) = 2πr1h
![]()
= 2 × 22 × 2 × 11
= 968 cm2.
(ii) Outer surface area of pipe (C.S.A) = 2πr2h
![]()
= 2 × 22 × 2.2 × 11
= 44 × 24.2
= 1064.8 cm2.
(iii) Total Surface area of Pipe (T.S.A.) = Inner CSA + Outer CSA + Area of circular ring.
= 2πr1h + 2πr2h + (2πr22h – 2πr12h)
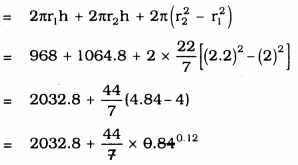
= 2032.8 + 5.28
∴ T.S.A. = 2038.08 cm2.
Question 4.
The diameter of a roller is 84 cm and its length is 120 m. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m2.
Solution:
Roller is in the form of cylinder.
Diameter, d = 84 cm,
![]()
l = h = 120 cm ⇒ 1.2 m.
∴ Curved surface area of Roller = 2 πrh
![]()
= 44 × 0.072
= 3.168 m2
∴ Area of 1 round of roller = 3.168 m2.
Area of 500 rounds … ? …
= 3.168 × 500
= 1584 m2.
∴ Total area of a playground is 1584 m2.
Question 5.
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs. 12.50 per m2.
Solution:
Diameter of cylindrical pole, d = 50 cm.
![]()
∴ r = 0.25 m
height of pole, h = 3.5 m.
Curved surface area of pole = 2πrh
![]()
= 44 × 0.25 × 0.5
= 5.5 m2.
Cost of painting for 1 m2 is Rs. 12.50,
Cost of painting for 5.5 m2 is … ? …
= 5.5 × 12.50
= Rs.68.75.
Question 6.
Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height.
Solution:
Curved surface arc of cylinder = 4.4 m2
radius, r = 0.7 m height, h = ?
C.S.A. of cylinder, A= 2πrh
2πrh = 4.4
![]()
44 × 0.1 × h = 4.4
4.4 h = 4.4
![]()
∴ h = 1 m.
Question 7.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
(i) its inner curved surface area.
(ii) the cost of plastering this curved surface at the rate of Rs. 40 per m2.
Solution:
Inner diameter of circular well, d = 3.5 m.
Radius, r = \(\frac{3.5}{2}\) m
Depth of the well – height, h = 10 m.
(i) Inner surfacer area of circular well, C.S.A. = 2πrh
C.S.A. = 2πrh
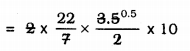
= 22 × 0.5 × 10
= 110 m2
(ii) Cost of plastering of area 1 m2 is Rs. 40
Cost of plastering 110 m2… ? …
= 110 × 40
= Rs. 4400.
Question 8.
In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
Solution:
Diameter of cylindrical pipe, d = 5 cm
= 0.5 m
![]()
Length of pipe = height, h = 28 m.
Curved surface area of pipe = ?
C.S.A.= 2πrh
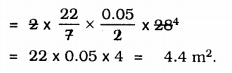
Question 9.
Find
(i) The lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) how much steel was actually used, if \(\frac{1}{12}\) of the steel actually used was wasted in making the tank.
Solution:
(i) Petrol tank is in the form of cylinder.
Diameter, d = 4.2 m
![]()
h = 4.5 m
TSA of petrol tank = 2πr(r + h)
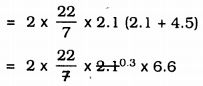
= 44 × 0.3 × 6.6
= 87.12 m2
(ii) ∴ Area of iron required for manufacturing tanker = 87.12 m2.
If iron used is 1 sq. m then there is a loss of \(\frac{1}{12}\).
Iron required except loss = \(1-\frac{1}{12}\)
= \(\frac{11}{12}\) m2
Area of \(\frac{11}{12}\) m2 is 87.12 m2.
Area of 1 m2 … ? …
![]()
= 95.04 m2.
Question 10.
In Fig. 13.12, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
Solution:
Diameter of cylindrical frame, d= 20 cm,
∴ r = 10 cm.
height, h = 30 cm.
For folding 2.5 cm is required.
∴ Total height = 30 + 2.5 + 2.5
= 35 cm.
Curved surface area of cloth covered, A
A= 2πrh
![]()
= 44 × 50
= 2200 cm2.
Question 11.
The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using card-board. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Solution:
Penholder is in the shape of a cylinder, which one of the edges is open and another is closed.
radius, r = 3 cm, height, h = 10.5 cm.
Total cardboard required by one Competitor: = Curved Surface Area + Area of bottom = 2πrh + πr2
![]()
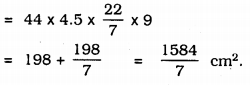
∴ Total cardboard required for 35 competitors is :