Karnataka Board Class 9 Maths Chapter 13 Surface Area and Volumes Ex 13.7
(Assume π = \(\frac{22}{7}\)unless stated otherwise)
Question 1.
Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm.
(ii) radius 3.5 cm, slant height 12 cm.
Solution:
(i) Volume of Cone, V = \(\frac{1}{3} \pi r^{2} h\)
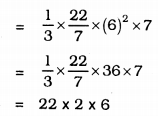
∴ V = 264 cm3.
(ii) r = 3.5 cm, h = 12 cm.
Volume of Cone, V = \(\frac{1}{3} \pi r^{2} h\)
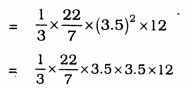
= 11 × 14
∴ V = 154 cm3.
Question 2.
Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm.
(ii) height 12 cm, slant height 13 cm.
Solution:
(i) radius, r = 7 cm, slant height, l = 25 cm
Volume of conical vessel, V = \(\frac{1}{3} \pi r^{2} h\)
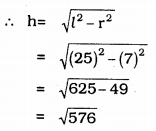
∴ h = 24 cm.
V = \(\frac{1}{3} \pi r^{2} h\)
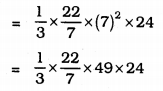
= 22 × 7 × 8
∴ V = 1232 cm3
∴ Volume of conical vessel
= \(\frac{1232}{1000}\) = 1.232 litres
(ii) height, h =12 cm, slant height, l = 13cm. r = ?, V = ? .
h2 = l2 – r2
∴ r2 = l2 – h2
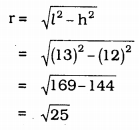
∴ r = 5 cm.
Volume of vessel, V = \(\frac{1}{3} \pi r^{2} h\)
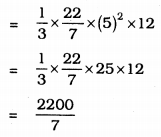
∴ V = 314.28 cm3.
In litres, = \(\frac{314.28}{1000}\) = 0.31428 litres.
Question 3.
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use π = 3.14)
Solution:
Height of the cone, h = 15 cm.
Volume, V = 1570 cm3, radius, r = ?
Volume of a cone. V = \(\frac{1}{3} \pi r^{2} h\)
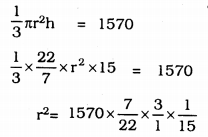
r2 = 100
∴ r = 10 cm.
Question 4.
If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Solution:
Volume of a right circular cone,V= 48π cm3,
height, h = 9 cm.
diameter, d = ?
Volume of cone, V = \(\frac{1}{3} \pi r^{2} h\)
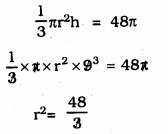
∴ r2 = 16
∴ r = 4 cm
∴ diameter, d = 2r
= 2 × 4
∴ d = 8 cm.
Question 5.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Solution:
d = 3.5m., h = 12 m., V = ?
![]()
Volume of Conical pit, V
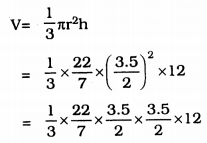
= 22 × 0.5 × 3.5
∴ V = 38.5 m3
V = 38.5 kilolitres
Question 6.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone.
Solution:
Volume of Cone, V = 9856 cm3
diameter of the base, d = 28 cm.
(i) h = ?,
(ii) I = ?,
(iii) C.S.A. = ?
(i) V = 9856 cm3.
d = 28 cm. ∴ r = \(\frac{28}{2}\) = 14 cm.
Volume of cone, V= \(\frac{1}{3} \pi r^{2} h\)
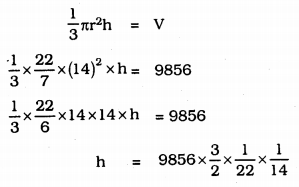
h = \(\frac{2688}{56}\)
h = 48 cm.
(ii) l2 = h2 + r2
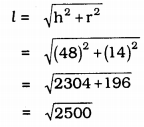
l = 50 cm.
(iii) Curved surface area of the cone, A
A = πrl
![]()
= 22 × 100
A= 2200 cm2.
Question 7.
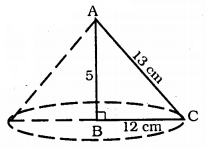
A right triangle ABC with sides 5 cm, 12 cm, and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
Cone is formed ∆ABC is revolved about the side 12 cm.
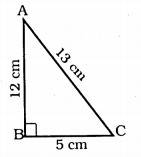
r = 5 cm,
h = 12 cm,
V = ?
Volume of Cone, V
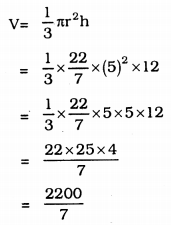
∴ V = 314.29 cm3.
Question 8.
If the triangle ABC in Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
Cone is formed when ∆ABC is revolved about 5 cm.
r = 12 cm,
h = 5 cm.
Volume of Cone, V
v = \(\frac{1}{3} \pi r^{2} h\)
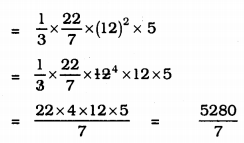
V = 754.28 cm3.
Volume of Cone in problem 7 = 314.29 cm3
Volume of Cone in problem 8 = 754.28 cm3
∴ ratio of both Volumes = \(\frac{314.29}{754.28}\)
= \(\frac{5}{2}\) = 5 : 12
Question 9.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find ifs volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Solution:
Diameter of heap of wheat in the form of Cone,
diameter, d = 10.5 m = \(\frac{21}{2}\)
![]()
height, h = 3 m. V = ?
Volume of Canvas Cover, V = \(\frac{1}{3} \pi r^{2} h\)
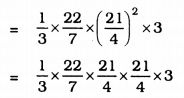
= 86.625 m3.
Area of Canvas required to cover a heap of wheat, C.S.A.
C.S.A.= πrl
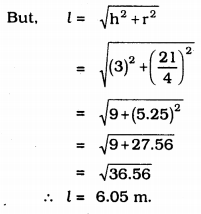
∴ Area of Canvas, A = πrl
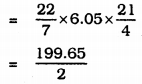
∴ A = 99.83 m2.