Students can Download Chapter 11 Perimeter and Area Ex 11.2, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2
Question 1.
Find the area of each of the following parallelograms :
a) 
Solution:
Base = B = 7cm
Height = h = 4 cm
∴ Area of the parallelogram = B × h
= 7 × 4 = 28 sq.cms
b) Base = B = 5 cm
Height = h = 3 cm.

Area of the parallelogram = Base × height
= B × h = 5 × 3
= 15 sq.cms
c) Base = B = 2.5 cms
Height = h = 3.5 cms
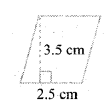
Area of the parallelogram
Base × height = 2.5 × 3.5 = 8.75 sq.cms
![]()
d) Base = B = 5 cms
Height = h = 4.8 cms

Area of the parallelogram = Base × height
= 5 × 4.8 = 24 sq.cms
e) Base = B = 2 cms

Height = h = 4.4 cms
∴ Area of the parallelogram = Base × height
2 × 4.4 = 8.8 sq.cms
Question 2.
Find the area of each of the following triangles :
Solution:
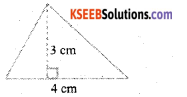
a) Base = B = 4 cms
Height = h = 3 cms

b) Base = B = 5cms
Height = h = 3.2 cms

∴ Area of the triangle
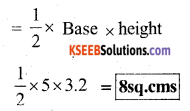
![]()
c) Base = B = 3 cms
Height = h = 4 cms
Area of the triangle


d) Base = B = 3 cms
Height = h = 2 cms
Area of the parallelogram
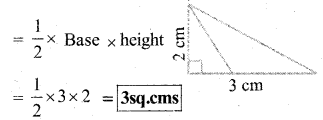
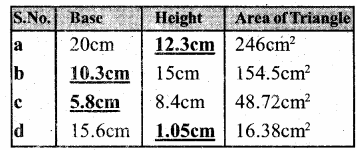
Question 3.
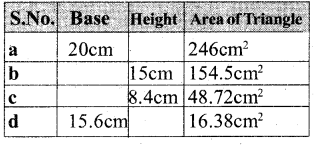
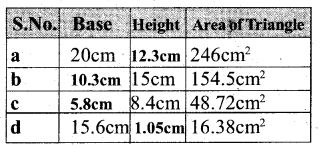
Find the missing values :
Solution:
a) Area of the parallelogram = Base × height
Base = 20 cm
Area = 246 sq cm
Height = ?
246 = 20 × h
![]()
Height = 12.3 cms
b) Height = 15 cm
Area = 154.5 cm2
Base = ?
Area of the parallelogram = Base × height
154.5 = B × 15
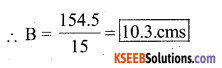
∴ Base = 10.3 cms
![]()
c) Height = 8.4 cm
Area = 48.72 cm2
Base = ?
Area of the parallelogram = Base × height
48.72 = B × 8.4
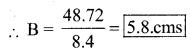
∴ Base = 5.8 cms
d) Base = 15.6 cm
Area = 16.38 sq cm
Height = ?
Area of the parallelogram = Base × height
16.38 = 15.6 × h

∴ Height = 1.05 cms
Question 4.
Find the missing values :
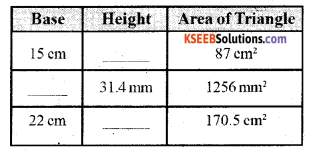
Solution:
i) Base = 15 cm Area = 87 cm2 Height = ?

ii) Height = 31.4 mm
Area = 1256 mm2
Base = ?

![]()
iii) Base = 22 cm Area = 170.5 cm2
Height = ?

Question 5.
PQRS is a parallelogram (Fig.23). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find :
Solution:
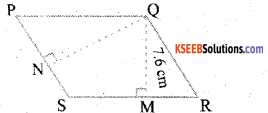
a) the area of the parallelogram PQRS
Area of the parallelogram PQRS = Base × height
Base = SR =12 cm
Height = QM = 7.6 cm
= 12 × 7.6 = 91.2 sq.cms
∴ Area = 91.2 cm2
b) QN, if PS = 8 cm
Base = PS = 8 cm Height = QN = ?
Area = 91.2 cm2
Area of the parallelogram = Base × height
91.2 = 8 × QN
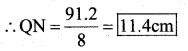
∴ QN = 11.4 cms.
Question 6.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (Fig 11.24). If the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BM and DL.
Solution:
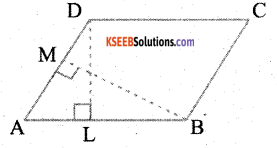
Area of the parallelogram = Base × height
i) Base = AB = 35 cm
Height = DL = ?
Area = 1470 cm2
1470 = 35 × DL
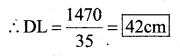
ii) Base = AD = 49 cm
Height = BM = ?
Area = 1470 cm2
Area of the parallelogram = Base × height
1470 = 49 × BM
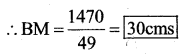
∴ BM = 30 cms.
![]()
Question 7.
∆ ABC is right-angled at A (Fig 11.25). AD Is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ∆ ABC. Also, find the length of AD.
Solution:
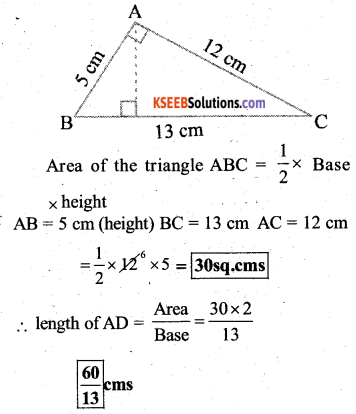
Question 8.
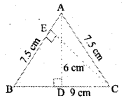
∆ ABC is isosceles with AB AC = 7.5 cm and BC = 9 cm (Fig 11.26). The height AD from A to BC is 6 cm. Find the area is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i.e., CE?
Solution:

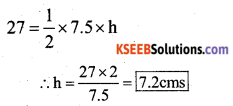
∴ The height from C to AB = CE = 7.2 cms