Students can Download Chapter 4 Simple Equations Ex 4.1, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 4 Simple Equations Ex 4.1
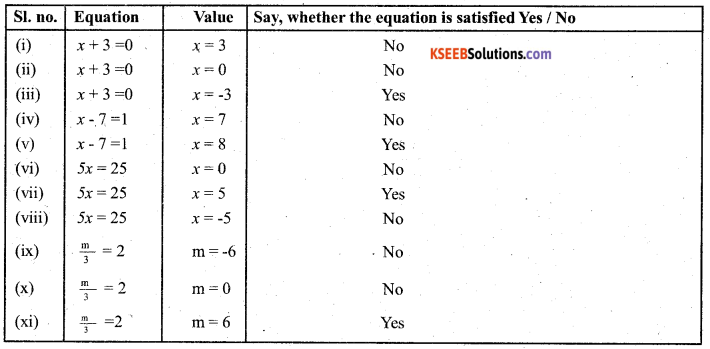
Question 1.
Complete the last column of the table.
Solution:
Question 2.
Check whether the value given in the brackets is a solution to the given equation or not :
a) n + 5 = 19 (n = 1)
Solution:
1 + 5 ≠ 19
6 ≠ 19
∴ LHS ≠ RHS
∴ n = 1 is not a solution to the given equation n + 5 = 19.
![]()
b) 7n + 5 = 19(n = -2)
Solution:
7 × -2 + 5 = 19
-14 + 5 = 19
-9 = 19
LHS ≠ RHS
∴ n = -2 is not a solutions the given equation 7n + 5 = 19 (n = 2)
7 × 2 + 5 = 19
14 + 5 = 19
19 = 19
LHS = RHS
∴ n = 2 is a solution to the given equation 7n + 5 = 19
c) 7n + 5 = 19 (n = 2)
Solution:
7 × 2+5 = 19
14 + 5 = 19
19 = 19
LHS = RHS
∴ n = 2 is a solution to the given equation 7n + 5 = 19.
d) 4p – 3= 13 (p = 1)
4(1) – 3 = 13
4 – 3 = 13
1 ≠ 13
LHS ≠ RHS
∴ p = 1 is not a solution to the given equation 4p – 3 = 13.
e) 4p – 3 = 13 (p = -4)
4(-4) – 3 = 13
– 16 – 3 = 13
-19 ≠ 13
LHS ≠ RHS
∴ p = -4 is not a solution to the given equation 4p – 3 = 13.
f) 4p – 3 = 13 (p = 0)
4(0) – 3 = 13
0 – 3 = 13
– 3 ≠ 13
LHS ≠ RHS
∴ p = 0 is not a solution to the given equation 4p – 3 = 13.
![]()
Question 3.
Solve the following equations by trial and error method :
i) 5p + 2 = 17
Solution:
If p = 0 then 5(0) + 2 = 17, 0 + 2 ≠ 17
If p = 1 then 5(1) + 2 = 17, 5 + 2 ≠ 17
If p = 2 then 5(2) + 2 = 17, 10 + 2 ≠ 17
If p = 3 then 5(3) + 2 = 17, 15 + 2 ≠ 17
∴ p = 3 is the solution to the given equation 5p + 2 = 17.
ii) 3m – 14 = 4
If m = 0 then 3(0) – 14
0 – 14 = – 14 ≠ 4
3m – 14 = 4
If m = 1 then 3(1) – 14
3 – 14 = -11
If m = 2 then 3(2) – 14
6 – 14 = – 8
If m = 3 then 3(3) – 14 = -5
If m = 4 then 3(4) – 14 = -2
If m = 5 then 3(5) – 14 = 1
If m = 6 then 3(6) – 14 = 4
LHS = RHS
∴ m = 6 is the solution to the given equation 3m – 14 = 4.
![]()
Question 4.
Write equations for the following statements :
i) The sum of numbers x and 4 is 9.
Solution:
x + 4 = 9
ii) 2 subtracted from y is 8.
Solution:
y – 2 = 8
iii) Ten times a is 70.
Solution:
10a = 70
iv) The number b divided by 5 gives 6.
Solution:
\(3 / 4 t=15\)
v) Three-fourth of t is 15.
Solution:
t = 15
vi) Seven times m plus 7 gets you 77.
Solution:
7m + 1 = 11
vii) One-fourth of a number x minus 4 gives 4.
Solution:
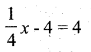
viii) If you take away 6 from 6 times y, you get 60.
Solution:
6y – 6 = 60
ix) If you add 3 to one-third of Z, you get 30.
Solution:
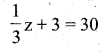
Question 5.
Write the following equations in statement forms :
i) p + 4 = 15
Solution:
The sum of P and 4 is equal to 15 .
ii) m – 7 = 3
Solution:
Seven subtracted from m is equal to 3.
iii) 2m = 1
Solution:
Two times a number m is equal to 7.
iv) \(\frac{\mathrm{m}}{5}\) = 3
Solution:
One – fifth of ‘m’ number is equal to 3 3m
v) \(\frac{\mathrm{3m}}{5}\) = 6
Solution:
Three – fifth of ‘m’ number is equal to 6
vi) 3p + 4 = 25
Solution:
Three times a number ‘P’ is added to 4 is equal to 25.
![]()
vii) 4p – 2 = 18
Solution:
Two is subtracted from 4 times ‘p’ is equal to 18.
viii)
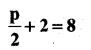
Solution:
Two is added to half number of p is equal to 8.
Question 6.
Set up an equation in the following cases:
i) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. (Take m to be the number of Parmit’s marbles.)
Solution:
Let the number of marbles Parmit had be ‘m’
∴ Number of marbles Irfan has = Five times of parmits marble 5m.
To this 7 marbles more means = 5m + 7
∴ 5m + 7 = 37.
![]()
ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. (Take Laxmi’s age to bey years)
Solution:
Let the age of Lakshmi be ‘y’ years
Three times of age = 3y
More than 4 years = 3y + 4
∴ Lakshmi’s father age be = 3y + 4
∴ 3y + 4 = 49
iii) The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. (Take the lowest score to be l.)
Solution:
Let the lowest score be ‘l’
Twice the lowest score be = 2l
Plus seven = 2l + 1
∴ The highest score = 2l + 7
∴ 2l + 7 = 87
iv) In an isosceles triangle, die vertex angle is twice either base angle. (Let the base angle be A in degrees. Remember that the sum of angles of a triangle is 180 degrees).
Solution:
Let the base angle be b°
Vertex angle = Twice the base angle
∴ Vertex angle = 2b
Sum of the angles of an isosceles triangle is =180°
∴ 2b + b + b = 180° = 4b = 180°