Students can Download Chapter 4 Simple Equations Ex 4.2, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 4 Simple Equations Ex 4.2
Question 1.
Given first the step you will use to separate the variable and then solve the equation:
a) x – 1 = 0
Solution:
The given equation = x – 1 = 0
Add 1 to both the sides
![]()
Checking
x – 1 = 0
put the value of x = 1
1 – 1 = 0
∴ LHS = RHS (checked)
b) x + 1 = 0
The given equation = x + 1 = 0
Subtract 1 from both the sides
![]()
Verification
x+ 1 = 0
substitute the value of x = -1 then x + 1 = 0
(-1) + 1 = 0
0 = 0
LHS = RHS (verified)
c) x – 1 = 5
The given equation is x – 1 = 5
Add 1 to both sides
![]()
Substitute the value in the equation x = 6.
x – 1 = 5
6 – 1 = 5
5 = 5
∴ LHS = RHS (verified)
![]()
d) x + 6 = 2
The given equation is x + 6 = 2
Subtract 6 from both the sides
![]()
Substitute the value of x = -4 in the given equation,
x + 6 = 2
-4 + 6 = 2
2 = 2
∴ LHS = RHS (verified)
e) y – 4 = -7
The given equation is y – 4 = -7
Add 4 to both the sides
![]()
substitute the value of y = -3 in the given equation
y – 4 = -7
-3 – 4 = -7
-7 = -7
∴ LHS = RHS (verified)
f) y – 4 = 4
Solution:
The given equation is y – 4 = 4
Add 4 to both the sides
![]()
substitute the value of y = 8 in the given equation
y – 4 = 4
8 – 4 = 4
4 = 4
∴ LHS = RHS (verified)
g) y + 4 = 4
Solution:
The given equation is y + 4 = 4
subtract 4 from both sides
![]()
substitute the value of y = 0 in the given equation.
y + 4 = 4
0 + 4 = 4
4 = 4
∴ LHS = RHS (verified)
h) y + 4 = -4
Solution:
The given equation is y + 4 = -4
subtract 4 from both the sides
![]()
y = -8 (verified)
substitute the value of y = -8 in the given equation
y + 4 = -4
-8 + 4 = -4
-4 = -4
∴ LHS = RHS (verified)
Question 2.
Give first the step you will use to separate the variable and then solve the equation:
a) 3l = 42
Solution:
The given equation is 3l = 42
Divide by 3 both the sides
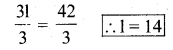
Substitute the value of l = 14 in the given equation
3l = 42
3(14) = 42
42 = 42
∴ LHS = RHS (verified)
![]()
b) \(\frac{\mathbf{b}}{2}\) = 6
Solution:
The given equation is \(\frac{\mathbf{b}}{2}\) = 6
Multiplied by 2 both the sides b
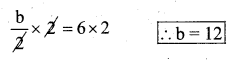
substitute the value of b = 12 in the given equation

∴ LHS = RHS (verified)
c)
\(\frac{\mathbf{p}}{7}\) = 4
Solution:
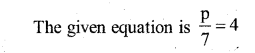
Multiplied by 7 to both the sides
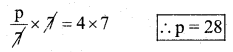
Substitute the value of p = 28 in the given equation

∴ LHS = RHS (verified)
d) 4x = 25
Solution:
The given equation is 4 x = 25
Divide both sides by 4
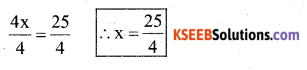
substitue the value of x = \(\frac{25}{4}\) in the given equation
4x = 25
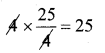
∴ LHS = RHS (verified)
e) 8y = 36
Solution:
The given equation is 8y = 36
Divide both sides by 8
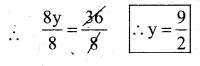
Substitute the equation by y = \(\frac{9}{2}\) in the given equation
8y = 36

∴ LHS = RHS
f)
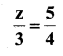
Solution:

Substitute the equation by z = \(\frac{15}{4}\) in the given equation
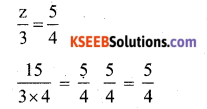
∴ LHS = RHS (verified)
g)
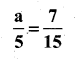
Solution:

Substitute the value of a = \(\frac{7}{3}\) in the given equation
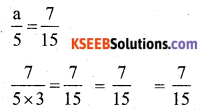
∴ LHS = RHS (verified)
h) 20t = -10
Solution:
The given equation is 20 t = -10
Divide by 20 to both sides
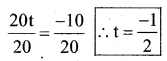

LHS = RHS (verified)
![]()
Question 3.
Given the steps you will use to separate the variable and then solve the equation:
a) 3n – 2 = 46
Solution:
The given equation is 3n – 2 = 46
Add 2 to both sides 3n – 2 + 2 = 46+ 2
3n = 48
Divide the equation by 3
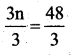
∴ n = 16 This is required solution.
substitute the value of n = 16 in the given equation
3n – 2 = 46
3(16) – 2 = 46
48 – 2 = 46
46 = 46
∴ LHS = RHS (verified)
b) 5m + 7 = 17
The given equation is 5m + 7 = 17
Subtract 7 from both sides
![]()
5m = 10
Divide the equation by 5 both the sides
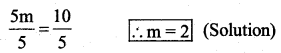
Substitute the value of m = 2 in the given equation
5m + 7 = 17
5(2) + 7 =17
10 + 7 = 17
∴ LHS = RHS (verified)
c) \(\frac{20 p}{3}\) = 40
Solution:

Substitute the value of p = 6 in the given equation. .

40 = 40
∴ LHS = RHS (verified)
d)
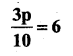
Solution:
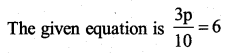
Multiply by 10 to both the sides
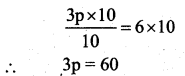
Divide by 3 to both sides

Substitute the value of p = 20 in the given equation

Question 4.
Solve the following equations :
a) 10p = 100
Solution:
The given equation is 10p = 100
Divide by 10 both the sides
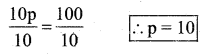
Substitute the value of p in the given equation
10p = 100
10 x 10 = 100
100 = 100
∴ LHS = RHS (verified)
![]()
b) 10p + 10 = 100
Solution:
The given equation is 10p + 10 = 100
subtract 10 from both the sides
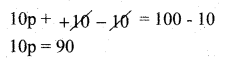
Divide by 10 both the sides
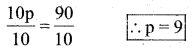
Substitute the value of p = 9 in the given equation
10p + 10 = 100
10 × 9 + 10 = 100
90 + 10 = 100
100 = 100
LHS = RHS (verified)
c) \(\frac{\mathbf{p}}{4}\) = 5
Solution:

5 = 5
∴ LHS = RHS (verified)
d) \(\frac{-p}{3}\) = 5
The given equation is \(\frac{-p}{3}\) = 5
The equation is multiplied by -3 both the sides
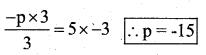
Substitute the value of p = -15 in the given equation

∴ LHS = RHS (verified)
e)
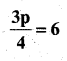
Solution:

Substitute the value p = 8 in the given equation

f) 3s = -9
The given equation is 3s = -9
Divide the equation by 3 both the sides

Substitute the value of s = -3 in the given equation
3s = -9
3(-3)=-9
-9 = -9
∴ LHS = RHS (verified)
g) 3s + 12 = 0
Solution:
The given equation is 3s + 12 = 0
subtract 12 from both the sides
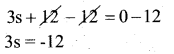
Divide by 3 both the sides

Substitute the value of s = -4 in the given equation
3s = 12 = 0
3(-4) = 12 = 0
-12 + 12 = 0
0 = 0
∴ LHS = RHS
h) 3s = 0
Solution:
The given equation is 3s = 0
Divide by 3 both the sides
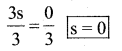
Substitute the value of s = 0 in the given equation
3s = 0
3(0) = 0
0 = 0
∴ LHS = RHS (verified)
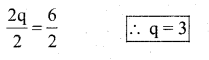
i) 2q = 6
Solution:
The given equation is 2q = 6
Divide the equation by 2 both the sides
![]()
substitute the value of q = 3 in the given equation
2q = 6
2(3) = 6 6 = 6
∴ LHS = RHS (verified)
![]()
j) 2q – 6 = 0
Solution:
The given equation is 2q – 6 = 0
Add 6 to both the sides
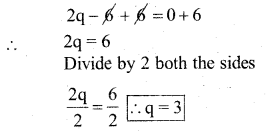
Substitute the value of q = 3 in the given equation
2q – 6 = 0
2(3) – 6 = 0
6 – 6 = 0
0 = 0
LHS = RHS (verified)
k) 2q + 6 = 0
Solution:
The given equation is 2q + 6 = 0
Subtract 6 from both the sides
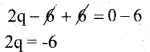
Divide by 2 both the sides by 2
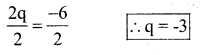
Substitute the value of q = -3 in the given equation
2q + 6 = 0
2(-3) + 6 = 0
-6 + 6 = 0
0 = 0
∴ LHS = RHS (verified)
l) 2q + 6 = 12
The given equation is 2q + 6 = 12
Subtract 6 from both the sides
![]()
Divide by 2 both the sides