Students can Download Chapter 6 The Triangles and Its Properties Ex 6.3, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.3
Question 1.
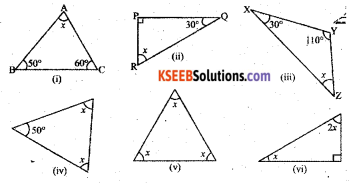
Find the value of the unknown x in the following diagrams :
Solution:
i) ∠A + ∠B + ∠C = 180°
x° + 50° + 60° = 180° (By Angle sum property of a triangle)
∠x + 110° = 180°
∠x = 180° – 110°
∠x = 70°
ii) ∠P + ∠Q + ∠R = 180°
90° + 30° + ∠x = 180° (By Angle sum property of a triangle)
120° + ∠x = 180°
∠x = 180° – 120° = 60°
iii) ∠X + ∠Y + ∠Z = 180°
Solution:
30° + 110° + ∠x = 180° (By Angle sum property of a triangle)
140° + ∠x = 180°
∴ ∠x = 180° – 140° = 40°
iv) 50° + x + x = 180°
50° + 2x = 180°
(By Angle sum property of a triangle)
2x = 180° – 50° = 130°
x = \(\frac{180^{\circ}}{2}\)
∴ ∠x = 60°
v) x + x + x = 180°
(By Angle sum property of a triangle)
3x = 180°
x = \(\frac{180^{\circ}}{2}\)
∴ x = 60°
![]()
vi) x + 2x + 90° = 180° (ByAngle sum property of a triangle)
3x = 180°
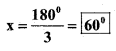
Question 2.
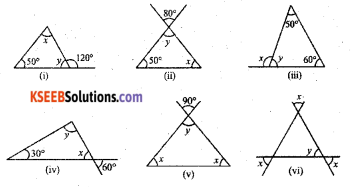
Find the values of the unknowns x and y in the following diagrams:
Solution:
i) x + 50° = 120° [By the exterior angle property of a triangle]
x= 120° – 50° = 7o°
By Angle sum property of a triangle
x + y + 50° = 180°
x + y = 180° – 50° = 130°
70° + y = 130°
y = 130° – 70° = 60°
∴ x = 70°, y = 60°
ii) 50° + y° + x° = 180°
∠y = 80° [vertically opposite angles]
50° + 80° + x° = 180° (Angle sum property of a triangle)
130° + x = 180°
x° = 180° – 130° = 50°
[∴ x = 50°, y = 80°]
![]()
iii) ∠x = 50° + 60° = 110° [By exterior – angle property of a triangle]
y + 50° + 60° = 180° ( By Angle sum property of a triangle)
y + 110° = 180°
∴ y = 180° – 110° = 70°
∴ y = 70°, x = 110°
iv) ∠x = 60° [vertically opposite angles]
30° + x° + y° = 180°
(By Angle sum property of a triangle)
30° + 60° + y° = 180°
90° + y° = 180°
∴ y°= 180° – 90° = 90°
∴ x = 60° y = 90°
v) ∠y = 90° [vertically opposite angles]
∠x + ∠x + ∠y = 180°
(Angle sum property of a triangle)
2x + y° = 180°
2x + 90° = 180°
2x = 180° – 90°= 90°
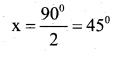
∴ ∠x = 45° & ∠y = 90°
![]()
vi) ∠x ∠y [vertically opposite angles]
∠x + ∠x + ∠y = 180°
(Angle sum property of a triangle)
2x + ∠y = 180°
2x + x° = 180° (∵ y = x)
3x = 180°
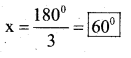
∴ x = 60° & y = 60°