KSEEB Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.5

Students can Download Chapter 6 The Triangles and Its Properties Ex 6.5, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.

Karnataka State Syllabus Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.5

Question 1.
PQR is a triangle, right-angled at P. If PQ = 10cm and PR = 24 cm, find QR.
Solution:

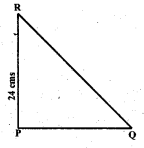
PQR is a right angled triangle. ∠RPQ = 90°
∴ QR² = PQ² + PR² (By pythagoras property)
= 10² + 24²
= 100 + 576
∴ QR =  = 26 cms

Question 2.
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution:

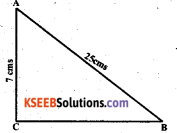
ABC is a right-angled triangle.
∠ACB = 90°
∴ AB² = AC² + BC² (By pythagoras property)
25² = 7² + BC²
BC² = 25² – 7² = 625 – 49
∴ BC = \(\sqrt{576}\) = 24
∴ BC = 24 cms

Question 3.
A 15m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
Solution:

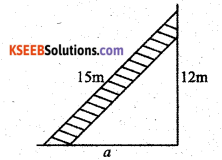
The distance of the foot of the ladder from the wall is ‘a’ m.
Then
a² + 12² = 12² (pythagoras property)
a² = 15² – 12²
a² = 225 – 144
a² = 81
∴ a = 
∴ The distance of the foot of the ladder from the wall be 9m.

Question 4.
Which of the following can be the sides of a right triangle?
Solution:
In the case of right-angled triangles, identify the right angles.
i) 2.5 cm, 6.5 cm, 6 cm
Solution:
The greatest side is hypotenuse = 6.5 cm
(2.5)² + (6)² = (6.5)² (According to Pythagoras property)
6.25 + 36 = 42.25
42.25 = 42.25
∴ This is a right-angled triangle. The given length can be the sides of a right-angled triangle. The right angle between the lengths of 2.5 cm and 6 cm.

ii) 2 cm, 2 cm, 5 cm
The greatest side is 5 cm
(2)² + (2)² = (5)² (According to pythagoras property)
4 + 4 ≠ 25
∴ It is not the lengths of right angled triangle.

iii) 1.5 cm, 2 cm, 2.5 cms
The greatest side is 2.5 cms.
According to pythagoras property
(2.5)² = (1.5)² + (2)²
6.25 = 2.25 + 4
6.25 = 6.25
It is a right angled trianges, the given lengths are sides of the right angled triangles.
∴ The right angle between the lengths of 1.5 cms and 2 cms.

Question 5.
A Tree is broken at a height of 5m from the ground and its top touches the ground at a distance of 12 m from the base tree. Find the original height of the tree.
Solution:

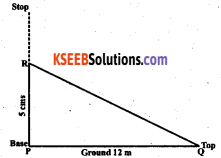
According to the given statement the sketch we get is right angled triangle
RQ² = PR² + PQ²
= 5² + 12²
= 25 + 144 = 169
∴ RQ =  = 13m
∴ The original height of the tree is PR + RS = 5 + 13 = 18 m

Question 6.
Angles Q and R of a ∆ PQR are 25° and 65°.
Write which of the following is true :
Solution:

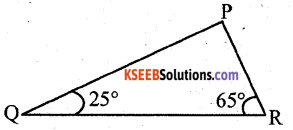
∠p = 90°
∴ According to Pythagoras property

ii) PQ² + RP² = QR²
PQ² + RP² = QR² is true

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Solution:

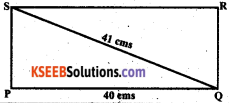
PQRS is a rectangle.
According to the figure, PQS is a right-angled triangle.
∴ QS² = PQ² + PS²
41² = 40² + PS²
∴ PS² = 42² + 40²
= 1681 – 1600
PS =  = 9 cms
The perimeter of the rectangle = 2 (PQ + PS)
= 2 (40 + 9) = 2 (49)
= 98 cms

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:

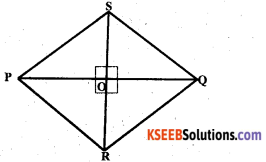
PQRS is a rhombus. The diagonals are PQ & RS.
PQ = 30 cms RS = 16 cms
According to fig In Rhombus the diagonals bisect
Each other. ∴ PQ & RS bisect at O.
PO = OQ SO = OR

Considering the ∆ POR
PR² = PO² + OR²
= 15² + 8²
= 225 + 64 = 289
∴ PR = \(\sqrt{289}\) = 17cms
∴ The perimeter of the rhombus = 4 × side PR
= 4 × 17 = 68 cms